RepQ-ViT: Scale Reparameterization for Post-Training Quantization of Vision Transformers
ICCV 2023
中国科学院自动化研究所
Abstract
RepQ-ViT,一种新的基于量化缩放因子(quantization scale)重参数化的PTQ框架
解耦量化和推理过程:
- 量化步骤部署了复杂的量化器
- 推理步骤采用量化缩放因子参数化的简化量化器
以保证精确的量化和高效的推理
重点关注具有极端分布的两个组件:
- LayerNorm后的activations
- 具有严重的通道间差异
- Softmax后的activations
- 幂律分布
关注的是对 activation 的量化方法
最初对两部分数据分别采用: channel-wise 量化 和 l o g 2 log\sqrt 2 log2 量化
推理时 将scale重参数化成硬件友好的 layer-wise 和 l o g 2 log 2 log2 量化
1. Introduction
影响ViT量化性能的关键组件: LayerNorm、Softmax 以及 GELU
作者将前人方法性能差的原因归结于:始终遵循着传统的量化范式,量化器的初始设计必须考虑未来的推理开销
作者指出:复杂的量化器和硬件标准并不总是对立的;相反,这两者可以通过 scale reparameterization 明确地联系起来
具体做法:在初始量化中使用复杂的量化器以充分保留原始的参数分布,然后通过尺度重新参数化将其转换为简单的硬件友好量化器进行实际推理,从而获得了较高的量化精度和推理效率。
对于LayerNorm之后的激活,我们首先使用逐通道量化来保持其严重的通道间变化,然后将尺度重新参数化到逐层量化以匹配硬件,这是通过调整LayerNorm的仿射因子和下一层的权重来实现的;
对于后Softmax激活,由于我们的研究表明它们的幂律分布和注意力分数的性质更倾向于log√2量化器,因此,我们感兴趣的是重新参数化尺度,将基改为2,以便在推理中实现比特移位操作。
涉及的量化器、计算范式包括:
- per-channel 量化
- per-Layer(per-Tensor)量化
- l o g 2 log\sqrt 2 log2 量化
- l o g 2 log\ 2 log 2 量化
![![[Pasted image 20240809122519.png]]](https://i-blog.csdnimg.cn/direct/cf01bfecdf304a7caf77fad65d52504c.png#pic_center)
2. Related Works
2.1. Vision Transformers
3. Methodology
Overview
主要的挑战是:将初始的复杂量化器转换为简单量化器进行推理
主要的点在于:将量化缩放因子重参数化
总体的算法如下图所示:

3.1. Preliminaries
ViTs’ standard structure
Y
l
−
1
=
MSA
(
LayerNorm
(
X
l
−
1
)
)
+
X
l
−
1
\begin{equation} Y_{l-1} = \text{MSA}(\text{LayerNorm}(X_{l-1})) + X_{l-1}\end{equation}
Yl−1=MSA(LayerNorm(Xl−1))+Xl−1
X
l
=
MLP
(
LayerNorm
(
Y
l
−
1
)
)
+
Y
l
−
1
\begin{equation} X_l = \text{MLP}(\text{LayerNorm}(Y_{l-1})) + Y_{l-1}\end{equation}
Xl=MLP(LayerNorm(Yl−1))+Yl−1
l = 1 , 2 , ⋯ , L l=1,2,\cdots, L l=1,2,⋯,L 是 Transformer Blocks 的数量
[
Q
i
,
K
i
,
V
i
]
=
X
′
W
q
k
v
+
b
q
k
v
i
=
1
,
2
,
.
.
.
,
h
\begin{equation} [Q_{i},K_{i},V_{i}]=X'W^{qkv}+b^{qkv} \quad i=1,2,...,h \\ \end{equation}
[Qi,Ki,Vi]=X′Wqkv+bqkvi=1,2,...,h
A
t
t
n
i
=
S
o
f
t
m
a
x
(
Q
i
⋅
K
i
T
D
h
)
V
i
\begin{equation} \mathrm{Attn}_{i}=\mathrm{Softmax}\left(\frac{Q_{i}\cdot K_{i}^{T}}{\sqrt{D_{h}}}\right)V_{i} \end{equation}
Attni=Softmax(DhQi⋅KiT)Vi
M
S
A
(
X
′
)
=
[
A
t
t
n
1
,
A
t
t
n
2
,
.
.
.
,
A
t
t
n
h
]
W
o
+
b
o
\begin{equation} \mathrm{MSA}(X')=[{\rm Attn}_{1},{\rm Attn}_{2},...,{\rm Attn}_{h}]W^{o}+b^{o}\\ \end{equation}
MSA(X′)=[Attn1,Attn2,...,Attnh]Wo+bo
M
L
P
(
Y
′
)
=
G
E
L
U
(
Y
′
W
1
+
b
1
)
W
2
+
b
2
\begin{equation} \mathrm{MLP}(Y')={\rm GELU}(Y'W^{1}+b^{1})W^{2}+b^{2} \end{equation}
MLP(Y′)=GELU(Y′W1+b1)W2+b2
量化矩阵乘法的所有权重和输入,保留LayerNorm和Softmax操作为浮点类型
也即,LayerNorm和Softmax本身的计算过程不做量化
Hardware-friendly quantizers
下面介绍几种常见的、硬件友好的量化器:
-
均匀量化器:
Q u a n t : x ( Z ) = c l i p ( ⌊ x s ⌉ + z , 0 , 2 b − 1 ) D e Q u a n t : x ^ = s ( x ( Z ) − z ) ≈ x \begin{align} \mathrm{Quant:} & x^{(\mathbb Z)}=\mathrm{clip}\left(\big \lfloor \frac{x}{s}\big\rceil+z,0,2^{b}-1\right)\\ \mathrm{DeQuant:}& \hat x=s\left(x^{(\mathbb Z)}-z\right)\approx x \end{align} Quant:DeQuant:x(Z)=clip(⌊sx⌉+z,0,2b−1)x^=s(x(Z)−z)≈x
其中, s ∈ R + s\in \mathbb R^{+} s∈R+ 是 量化缩放因子, z ∈ Z z\in \mathbb Z z∈Z 是 零点,二者都取决于 x x x 的上下界,具体计算公式如下:
s = m a x ( x ) − m i n ( x ) 2 b − 1 , z = ⌊ − m i n ( x ) s ⌉ \begin{align} s=\frac{{max(x)-min(x)}}{{2^{b}-1}},\quad z=\Big\lfloor -\frac{min(x)}{s} \Big\rceil \end{align} s=2b−1max(x)−min(x),z=⌊−smin(x)⌉ -
log2量化器:
本文中仅将其用于 Softmax 后的 activation,因此,仅仅考虑 对正数 的量化:
Q u a n t : x ( Z ) = c l i p ( ⌊ − log 2 x s ⌉ , 0 , 2 b − 1 ) D e Q u a n t : x ^ = s ⋅ 2 − x ( Z ) ≈ x \begin{align} \mathrm{Quant:} x^{(\mathbb Z)}&=\mathrm{clip}\left(\big \lfloor -\log_{2} \frac{x}{s}\big\rceil,0,2^{b}-1\right) \\ \mathrm{DeQuant:} \hat x &= s \cdot 2^{-x^{(\mathbb Z)}} \approx x \end{align} Quant:x(Z)DeQuant:x^=clip(⌊−log2sx⌉,0,2b−1)=s⋅2−x(Z)≈x
log2函数和base - 2幂函数都可以通过快速高效的比特移位操作实现
log2运算可以近似对应寻找数值中最左侧的’1’的位置
位运算的奇技淫巧(二) - RioTian - 博客园 (cnblogs.com)
对于以上量化器的应用粒度,权重的通道级量化和激活的层级量化可以平衡精度和效率
3.2. Scale Reparam for LayerNorm Activations
LayerNorm的计算公式:
LayerNorm
(
X
n
,
:
)
=
X
n
,
:
−
E
[
X
n
,
:
]
V
a
r
[
X
n
,
:
]
+
ϵ
⊙
γ
+
β
\text{LayerNorm}(X_{n,:})=\frac{X_{n,:}-E[X_{n,:}]}{\sqrt{Var[X_{n,:}]+\epsilon}}\odot \gamma + \beta
LayerNorm(Xn,:)=Var[Xn,:]+ϵXn,:−E[Xn,:]⊙γ+β
其中,
n
=
1
,
2
,
⋯
,
N
,
E
[
X
n
,
:
]
n=1,2,\cdots,N,\ E[X_{n,:}]
n=1,2,⋯,N, E[Xn,:] 和
V
a
r
[
X
n
,
:
]
Var[X_{n,:}]
Var[Xn,:] 分别是 均值 和 方差
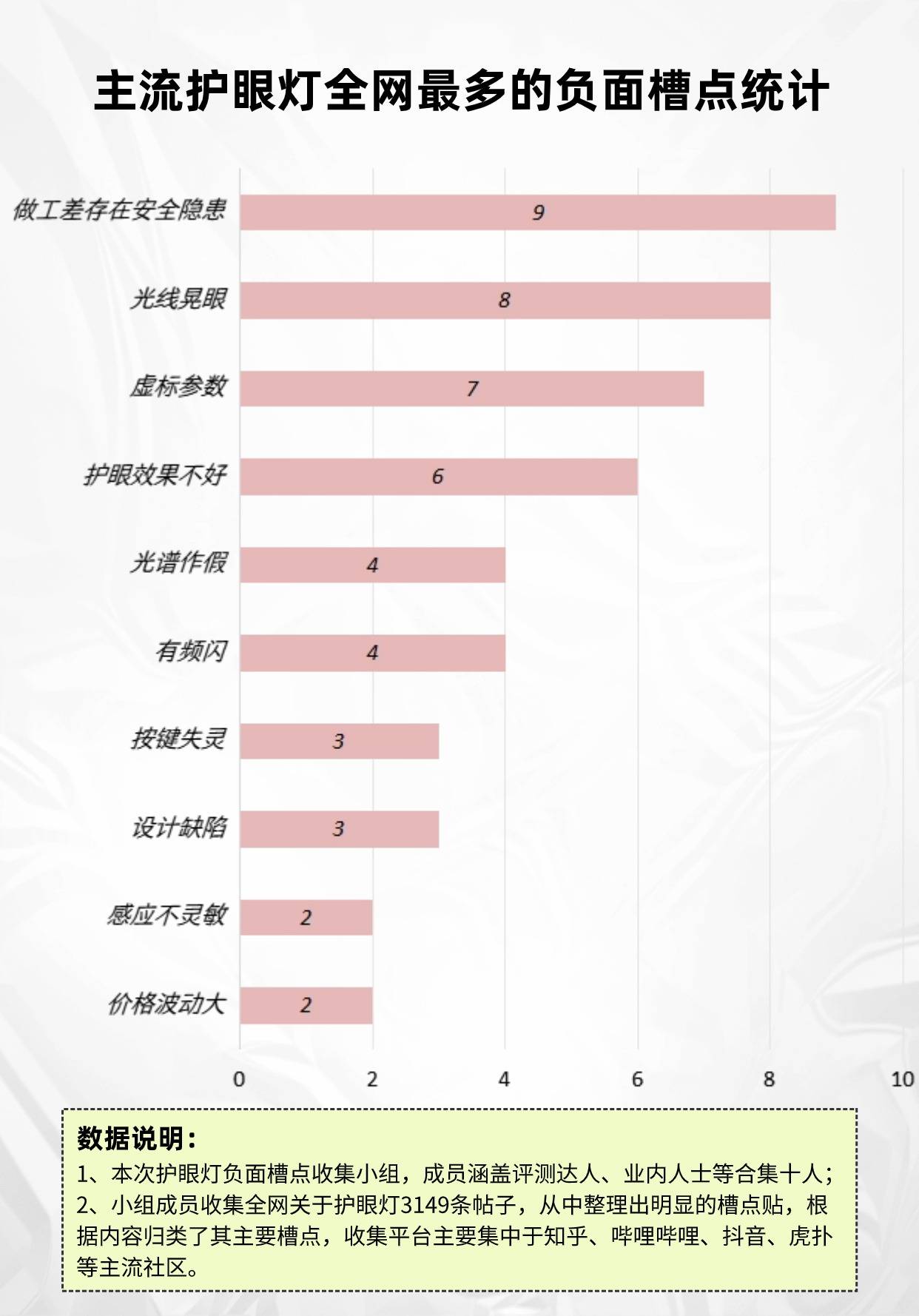
通过对LayerNorm后激活的研究,我们发现它们具有严重的通道间差异,这是对量化性能的一个重要限制
![![[Pasted image 20240809152633.png]]](https://i-blog.csdnimg.cn/direct/ca83308769aa4d11943495baa3ba8bf0.png#pic_center)
上图为 DeiT-S 中 第1个模块 LayerNorm 后 激活 的 第300~350通道 的分布箱线图
简单地将统一的量化尺度应用于每个通道的逐层量化不能适应如此严重的通道间差异,从而导致显著的精度下降
提出一种将通道量化转换为层量化的LayerNorm后激活 scale reparameterization 方法
具体做法是,首先通过 通道级 量化获取 scale 和 zero-point
s
∈
R
D
,
z
∈
Z
D
\boldsymbol{s}\in R^{D},\ \boldsymbol{z}\in Z^{D}
s∈RD, z∈ZD
将其重参数化为
s
~
=
s
~
⋅
1
,
z
~
=
z
~
⋅
1
\boldsymbol{\widetilde s}=\widetilde s\cdot\boldsymbol{1},\ \boldsymbol{\widetilde z}=\widetilde z\cdot\boldsymbol{1}
s
=s
⋅1, z
=z
⋅1
文中将
s
~
,
z
~
\widetilde s, \widetilde z
s
,z
设为相应的均值,
s
~
=
E
(
s
)
,
z
~
=
E
(
z
)
\widetilde s=E(\boldsymbol{s}), \ \widetilde z=E(\boldsymbol{z})
s
=E(s), z
=E(z)
定义 variation factors
r
1
=
s
/
s
~
r_{1}=s / \widetilde s
r1=s/s
,
r
2
=
z
−
z
~
r_{2}=z-\widetilde z
r2=z−z
代入(9)可得,
z
~
=
z
−
r
2
=
⌊
−
[
min
(
X
:
,
d
′
)
]
1
≤
d
≤
D
+
s
⊙
r
2
s
⌉
(
13
)
\widetilde z=z-r_{2}=\Big\lfloor - \frac{[\min(X'_{:,d})]_{1\le d\le D}+s\odot r_{2}}{s} \Big\rceil\quad(13)
z
=z−r2=⌊−s[min(X:,d′)]1≤d≤D+s⊙r2⌉(13)
s
~
=
s
r
1
=
[
max
(
X
:
,
d
′
)
−
min
(
X
:
,
d
′
)
]
1
≤
d
≤
D
/
r
1
2
b
−
1
(
14
)
\widetilde s=\frac{s}{r_{1}}=\frac{[\max(X'_{:,d})-\min(X'_{:,d})]_{1\le d\le D}/r_{1}}{2^{b}-1}\quad(14)
s
=r1s=2b−1[max(X:,d′)−min(X:,d′)]1≤d≤D/r1(14)
对 LayerNorm 的 仿射因子 以及 下一层的权重和偏移值 做 可解释性的调整,可以将 channel-wise 量化得到的 quantization scale 和 zero-point 重参数化为 Layer-wise 的 quantization scale 和 zero-point(设置为原始向量的均值)
同时需要再做 Calibration 进行调整
对LayerNorm:
β
~
=
β
+
s
⊙
r
2
r
1
,
γ
~
=
γ
r
1
\begin{align} \widetilde \beta=\frac{{\beta+s\odot{r_{2}}}}{{r_{1}}},\quad \widetilde\gamma=\frac{\gamma}{r_{1}} \end{align}
β
=r1β+s⊙r2,γ
=r1γ
对下一层参数:
W
~
:
,
j
q
k
v
=
r
1
⊙
W
:
,
j
q
k
v
b
~
j
q
k
v
=
b
j
q
k
v
−
(
s
⊙
r
2
)
W
:
,
j
q
k
v
\begin{align} \widetilde{W}^{qkv}_{:,j}&=r_{1}\odot W_{:,j}^{qkv} \\ \widetilde{b}^{qkv}_{j}&=b_{j}^{qkv}-(s\odot r_{2})W_{:,j}^{qkv} \end{align}
W
:,jqkvb
jqkv=r1⊙W:,jqkv=bjqkv−(s⊙r2)W:,jqkv
3.3. Scale Reparam for Softmax Activations
Softmax后激活,具有远离高斯和拉普拉斯分布的幂律分布,这是极不平衡的,因此被确定为量化的另一个关键障碍

大部分激活集中在相对较小的数值上,只有少数激活离散分布在较大的数值(接近1)上
较大的数值反映了块之间的重要相关性,必须在量化过程中很好地保留它们
前人使用 log2 量化器 对 Softmax 后激活进行量化,然而,这种方式 对重要注意力分数的描述过于稀疏。
例如:
[
2
−
1.5
,
2
−
0.5
]
[2^{-1.5},\ 2^{-0.5}]
[2−1.5, 2−0.5] 之间的数都会被舍入成
2
−
1
2^{-1}
2−1
而 log√2量化器为大值提供了更高的量化分辨率,可以更准确地描述分布
缺点是:对硬件不友好
将 log 2 \log \sqrt 2 log2 量化器 转换为 log 2 \log 2 log2 量化器:
A ( Z ) = clip ( ⌊ − log 2 A s ⌉ , 0 , 2 b − 1 ) = clip ( ⌊ − 2 log 2 A s , 0 , 2 b − 1 ) \begin{align} A^{(\mathbb Z)}&=\text{clip}\left(\lfloor -\log_{\sqrt 2} \frac{A}{s} \rceil,0,2^{b}-1\right) \\ &=\text{clip}\left(\lfloor -2\log_{2} \frac{A}{s},0,2^{b}-1\right) \end{align} A(Z)=clip(⌊−log2sA⌉,0,2b−1)=clip(⌊−2log2sA,0,2b−1)
A ^ = s ⋅ 2 − A ( Z ) 2 = { s ⋅ 2 − A ( Z ) 2 A ( Z ) = 2 k , k ∈ Z s ⋅ 2 − A ( Z ) + 1 2 ⋅ 2 A ( Z ) = 2 k + 1 , k ∈ Z = s ⋅ 2 ⌊ − A ( Z ) 2 ⌋ ⋅ [ 1 ( A ( Z ) ) ⋅ ( 2 − 1 ) + 1 ] \begin{align} \hat A&=s\cdot 2^{- \frac{{A^{(\mathbb Z)}}}{{2}}}\\ &=\begin{cases} s\cdot 2^{- \frac{{A^{(\mathbb Z)}}}{{2}}}\quad &A^{(\mathbb Z)}=2k,k\in \mathbb Z\\ s\cdot 2^{- \frac{{A^{(\mathbb Z)}+1}}{{2}}}\cdot \sqrt 2 \quad &A^{(\mathbb Z)}=2k+1,k\in \mathbb Z\\ \end{cases}\\ &=s\cdot 2^{\lfloor - \frac{A^{(\mathbb Z)}}{2} \rfloor}\cdot [\mathbb 1(A^{(\mathbb Z)})\cdot(\sqrt 2-1)+1] \end{align} A^=s⋅2−2A(Z)={s⋅2−2A(Z)s⋅2−2A(Z)+1⋅2A(Z)=2k,k∈ZA(Z)=2k+1,k∈Z=s⋅2⌊−2A(Z)⌋⋅[1(A(Z))⋅(2−1)+1]
经过上述分析,只需将 量化缩放因子 做如下 处理:
s
~
=
s
⋅
[
1
(
A
(
Z
)
)
⋅
(
2
−
1
)
+
1
]
\widetilde s=s\cdot [\mathbb 1(A^{(\mathbb Z)})\cdot(\sqrt 2-1)+1]
s
=s⋅[1(A(Z))⋅(2−1)+1]
4. Experiments

,