内容介绍
给你一个正整数
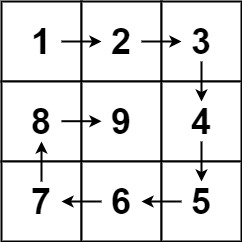
n,生成一个包含1到n2所有元素,且元素按顺时针顺序螺旋排列的n x n正方形矩阵matrix。示例 1:
输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2:
输入:n = 1 输出:[[1]]提示:
1 <= n <= 20
完整代码
class Solution {
public int[][] generateMatrix(int n) {
int l = 0, r = n - 1, t = 0, b = n - 1;
int[][] mat = new int[n][n];
int num = 1, tar = n * n;
while(num <= tar){
for(int i = l; i <= r; i++) mat[t][i] = num++; // left to right.
t++;
for(int i = t; i <= b; i++) mat[i][r] = num++; // top to bottom.
r--;
for(int i = r; i >= l; i--) mat[b][i] = num++; // right to left.
b--;
for(int i = b; i >= t; i--) mat[i][l] = num++; // bottom to top.
l++;
}
return mat;
}
}
思路详解
代码功能
这段代码定义了一个名为Solution的类,其中包含一个名为generateMatrix的方法。该方法用于生成一个按顺时针顺序填充的n阶矩阵,矩阵中的元素从1开始递增,直到n*n。
思路详解
-
初始化边界变量
l和r分别表示矩阵的左边界和右边界,初始值分别为0和n-1。t和b分别表示矩阵的顶部边界和底部边界,初始值分别为0和n-1。
-
创建矩阵
- 使用
new int[n][n]创建一个n阶矩阵mat,用于存储填充的元素。
- 使用
-
初始化填充变量
num表示当前要填充的数字,初始值为1。tar表示填充的目标值,即n*n。
-
循环填充矩阵
- 使用
while循环,当num小于等于tar时,继续填充矩阵。
- 使用
-
按顺时针顺序填充矩阵
- 从左到右填充顶部行:使用
for循环,从左边界l到右边界r,填充顶部行mat[t][i],并将num递增。 - 从上到下填充右侧列:使用
for循环,从顶部边界t到底部边界b,填充右侧列mat[i][r],并将num递增。 - 从右到左填充底部行:使用
for循环,从右边界r到左边界l,填充底部行mat[b][i],并将num递增。 - 从下到上填充左侧列:使用
for循环,从底部边界b到顶部边界t,填充左侧列mat[i][l],并将num递增。
- 从左到右填充顶部行:使用
-
更新边界
- 在每完成一轮填充后,更新边界变量:顶部边界
t向下移动一位(t++),右边界r向左移动一位(r--),底部边界b向上移动一位(b--),左边界l向右移动一位(l++)。
- 在每完成一轮填充后,更新边界变量:顶部边界
-
返回填充后的矩阵
- 当
num大于tar时,循环结束,返回填充好的矩阵mat。
- 当
总结
这段代码通过不断缩小矩阵的边界,并在每轮循环中按照顺时针顺序填充矩阵,最终生成一个按顺时针顺序递增的n阶矩阵。整个算法的时间复杂度为O(n^2),空间复杂度为O(n^2),适用于需要生成螺旋矩阵的场景
知识点精炼
矩阵初始化
- 使用
int[n][n]声明并初始化一个二维数组,用于存储螺旋矩阵的元素。
2. 边界控制
- 使用四个变量
l(左边界)、r(右边界)、t(上边界)、b(下边界)来控制矩阵的填充范围。
3. 循环填充
- 使用
while循环,条件为当前填充数字num小于等于矩阵元素总数tar(即n*n)。
4. 顺时针填充顺序
- 顶部行:从左到右填充,更新上边界
t。 - 右侧列:从上到下填充,更新右边界
r。 - 底部行:从右到左填充,更新下边界
b。 - 左侧列:从下到上填充,更新左边界
l。
5. 边界收缩
- 在每轮填充后,相应地调整边界变量的值,以缩小下一次填充的范围。
6. 返回结果
- 当填充完毕,返回填充好的二维数组
mat。
7. 算法效率
- 时间复杂度:O(n^2),因为每个元素都需要填充一次。
- 空间复杂度:O(n^2),用于存储矩阵的二维数组。
8. 编程技巧
- 使用嵌套
for循环实现矩阵的顺时针填充。 - 通过边界变量的调整,简化循环逻辑,避免复杂的条件判断。
扩展:如何避免填充重复数字
在给出的代码中,填充重复数字通常是由于边界调整不当导致的。为了确保每个数字只填充一次,需要仔细管理边界变量的更新。以下是避免填充重复数字的几个关键点:
-
更新边界前检查:在每轮填充完成后,确保在更新边界之前,新边界不会与旧边界重叠。
-
避免边界重叠:在每次循环结束时,更新边界之前,应该检查是否已经到达了矩阵的极限边界,以避免重叠。
以下是修改后的代码,其中包含了避免填充重复数字的逻辑:
class Solution {
public int[][] generateMatrix(int n) {
int l = 0, r = n - 1, t = 0, b = n - 1;
int[][] mat = new int[n][n];
int num = 1, tar = n * n;
while(num <= tar){
// 从左到右填充顶部行
for(int i = l; i <= r; i++) mat[t][i] = num++;
t++; // 更新上边界
// 从上到下填充右侧列
for(int i = t; i <= b; i++) mat[i][r] = num++;
r--; // 更新右边界
// 确保底部行未被填充
if(t <= b) {
// 从右到左填充底部行
for(int i = r; i >= l; i--) mat[b][i] = num++;
b--; // 更新下边界
}
// 确保左侧列未被填充
if(l <= r) {
// 从下到上填充左侧列
for(int i = b; i >= t; i--) mat[i][l] = num++;
l++; // 更新左边界
}
}
return mat;
}
}
在上述代码中,我添加了两个if语句来检查在填充底部行和左侧列之前,新的上边界t是否已经超过了下边界b,以及新的左边界l是否已经超过了右边界r。这样可以确保在矩阵的最后一行和最后一列时不会重复填充。
通过这种方式,我们可以确保每个数字只被填充一次,避免了任何可能的重复填充问题。