概论

1.1 基本概念和术语

1.1.1 基本概念

计算机处理的的是数值性数据，当计算机处理用户信息表中的数据的时候，需要弄清3个问题

1.数据的逻辑结构

数据之间存在怎样的内在联系，数据中，有且只有一个是首节点/尾结点，其他节点有且只有一个相邻的位于它之前和之后的结点

2.数据的存储结构

数据在计算机的存储方式称为存储结构。在C语言中，最常见的是用结构数组来存储整个用户的信息表，每一个结构数组元素也是一个结构，用于表示信息用户的一个结点。用户信息表中相邻的结点，对应结构数组中的元素也是连续的，在这种存储方式下，逻辑相邻的结点就必须是物理相邻，被称为顺序存储，还有其他存储方式。

3.数据的运算合集

对数据的存储一定会涉及到相关的运算。在用户的信息表中，可以进行删除一个用户、增加有一个用户、查找某个用户。应该明确指出这些操作的含义。为一批数据定义的所有运算（或称操作）构成一个运算（操作）集合。

数据结构就是按照一定的逻辑结构组成的一批数据，使用某种存储方式将数据存储在计算机中，并在这些数据上定义了一个运算集合

1.1.2数据的逻辑结构（数据结构）

数据的逻辑结构是数据与数据之间存在的逻辑关系，用一个二元组来表示
$$
B=(K,R)\K代表数据（结点的有限集合），R是集合K上关系的有限集合
$$
例如：5个人，a，b，c，d，e，a是b的父亲，b是c的父亲，c是d的父亲，d是e的父亲，讨论它们之间的父子关系，可以表达为B=（K，R），其中K={a,b,c,d,e},R={r},r={<a,b>,<b,c>,<c,d>,<d,e>}.

也可以用图形表示

ki∈K,Kj∈K，<ki,kj>∈r,ki是kj的前驱，kj是ki的后继。

若某个结点没有前驱，就是开始结点；没有后继结点，就是终端结点；既不是开始也不是终端的为内部结点。

线性结构:一个前驱，一个后继

树型结构：一个前驱，多个后继

图型结构：多个前驱，多个后继

1.1.3数据的存储结构

数据的逻辑结构是独立于计算机的，与在计算机中的存储是无关的，要对数据进行处理，就必须对数据进行存储，数据的存储结构主要有4种存储方式

（1）顺序存储

通常存储线性结构的数据，使逻辑相邻的结点一定是物理位置相邻

（2）链式存储

给每一个结点附加一个指针段，指的是该结点的后继存储地址，一个结点可以有一个后继，也可以有多个后继，所以可以有一个指针域，也可以有多个指针，逻辑相邻的结点在存储区域中可以不是物理相邻。

（3）索引存储

在线性结构中，以开始结点为索引号1，其他结点的索引号依次加1，每个结点都有唯一的索引号，根据索引号确定存储地址。

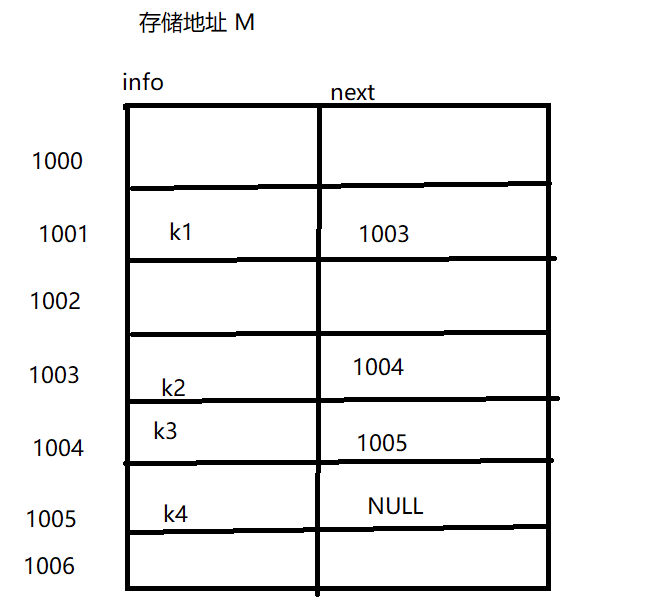
（4）散列存储

构造一个从集合K到存储区域M的函数h，定义域为K，值域为M，存储地址由h（Ki）决定

一个数据结构存储在计算机中，整个数据所占的存储空间不一定小于数据本身所占的存储空间，通常把数据本身所占的存储空间和整个数据结构所占的存储空间的大小的比值叫做存储密度，显然，数据结构的存储密度不大于1，线性结构存储密度为1，链式结构小于1。

1.2 数据类型和抽象数据类型

1.2.1数据类型

数据类型（简称类型）反映了数据的取值范围以及这类数据可以施加的运算。一个数据类型就是同一类数据的全体，是数据的一种属性，规定了数据的可变化范围，

1.2.2抽象数据类型

这是一种和表示无关的数据类型，是一个数据模型及定义在该模型的一组运算，定义一个抽象数据类型时，必须给出它的名字及运算符名，及函数名，并规定参数性质。（c++中的类支持抽象数据类型）

简言说明，就是自定义类型。

1.3算法和算法分析

解决某个问题的方法和步骤就叫做算法

特征

（1）有穷性：算法执行要在有限步内进行

（2）确定性：每个步骤是确定的，无二义性

（3）输入：可以有0个或多个输入

（4）输出：一定有输出结果

（5）可行性：每一个步骤都是可行的

1.3.1时间复杂度和空间复杂度

一个算法和优劣是从算法的执行时间和所用的存储空间两个方面衡量的。

(1)时间复杂度

由于算法在不同机器上执行时间不同，资源占用情况也不一样。所以时间复杂度使用算法执行过程中的基本操作次数来衡量的，使用大O渐进表示（O（）），在评价算法的时间复杂度时，只关系算法的本质区别，不考虑细小区别。

常数阶 31 O（1）

线性阶 2*n+17 O（n）

平方阶 n^2+10 O(n^2)

立方阶 2*n^3 O(n^3)

常见的算法时间复杂度

O（1）<O(log n)<O(n)<O(n*log n)<O(n2)<O(n3)<……<O(2^n)

（2）空间复杂度

除了数据以外附加的存储空间，度量方法与时间复杂度类似