Using the ST-LINK/V2-1 to program and debug the STM32 on board
news2026/2/15 3:17:16
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2043423.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
UE5学习笔记14-动画的混合空间
零、我看视频中使用的是UE5.0左右的版本,我使用的是UE5.4,5.4中创建混合空间,没有看见有2D和3D混合动画空间的区分,具体的UE5如何创建2D的动画暂时不知道(我感觉现在创建的是3D的动画)
一、创建混合空间 1.我将所有的动画蓝图和动…
vue用户管理、角色管理和部门管理展示
1、用户和角色一对多,用户和部门多对多
2、用户管理 编辑用户时部门层级展示 角色-下拉框展示 <template><div class"s"><!-- 操作按钮 --><div class"shang"><el-input v-model"searchText" placeholde…
EXTI外部中断之对射式红外传感器计次应用案例
系列文章目录
STM32中断系统之EXTI外部中断 文章目录 系列文章目录前言一、应用案例简介二、电路接线图三、应用案例代码四、应用案例分析4.1 配置外部中断4.1.1 配置RCC时钟4.1.2 配置GPIO4.1.3 配置AFIO4.1.4 配置EXTI4.1.5 配置NVIC 4.2 编写中断函数 前言
提示࿱…
泛微OA系统走进腾讯大厦
企业信息化、数字化、网络化、智能化的快速发展带来了无限可能,但同时也带来了系统安全的严峻挑战。您准备好应对了吗?
上月由腾讯安全部、泛微联合举办的“OA 系统安全防护与腾讯iOA 零信任安全策略客户会”在腾讯滨海大厦成功举办,本次活动邀请了60位…
拆开一个断了FPC的墨水屏,是不是像OLED一样驱动芯片在里面
可对比查看一个OLED的屏幕拆解
拆解理由
第一次焊接驱动板时的fpc上下接问题,但焊接到板子上并没有达到正常的显示效果。PI补强也被撕下来。后来拔下来后发现金手指断裂。本来想用一个fpc排线连接在一起,但后来发现并没有达到理想效果,飞线…
【Python学习-UI界面】PyQt5 小部件14-QDock 子窗口
可停靠窗口是一个子窗口,可以保持浮动状态或附加到主窗口的指定位置。 QMainWindow类的主窗口对象保留了一块区域供可停靠窗口使用。该区域位于中央窗口部件周围。
可停靠窗口可以在主窗口内移动,也可以被取消停靠并由用户移动到新的区域。
样式如下: …
MinIO DataPOD 目标锁定 GPU Direct 并行文件系统
MinIO 推出针对 AI 应用的 DataPOD 参考架构
MinIO 设计了一种旨在为 AI 训练提供数据的 exascale DataPOD 参考架构。这家开源对象存储软件供应商正将其可扩展至100 PiB(即大约112.6 PB)的单元定位为一种替代方案,以取代使用 GPU Direct 技…
新中地2402期GIS特训营学员圆满结业,解锁GIS开发的无限可能!
GIS开发了解
24年8月5日,新中地GIS开发特训营2402期学员迎来了属于自己的结业典礼。 初入特训营,教与学双向奔赴
从24年3月4日开班,面对全新的领域,大家新中既有对未知的忐忑,更有对掌握GIS开发技术的期待 在本期学员…
车辆车载客流统计系统解决方案
车辆车载客流统计系统是一种用于实时监测和分析乘客流量的技术解决方案,它可以帮助公交公司、地铁运营商等交通管理部门优化运营计划、提高服务效率和乘客满意度。以下是一个详细的车载客流统计系统解决方案:
一、系统组成 传感器与设备 摄像头…
C库函数signal()信号处理
signal()是ANSI C信号处理函数,原型如下:
#include <signal.h>typedef void (*sighandler_t)(int);
sighandler_t signal(int signum, sighandler_t handler);
signal()将信号signum的处置设置为handler,该handler为SIG_IGNÿ…
脊髓损伤治疗方法和需要那些营养
脊髓损伤作为一种严重的神经系统损伤,其治疗与康复一直是医学界关注的重点。在中医领域,针对脊髓损伤的治疗有着独特的理论和方法,旨在通过调节人体内部环境,促进受损神经的修复与再生。以下将从中医缓解方法与营养支持两个方面进…
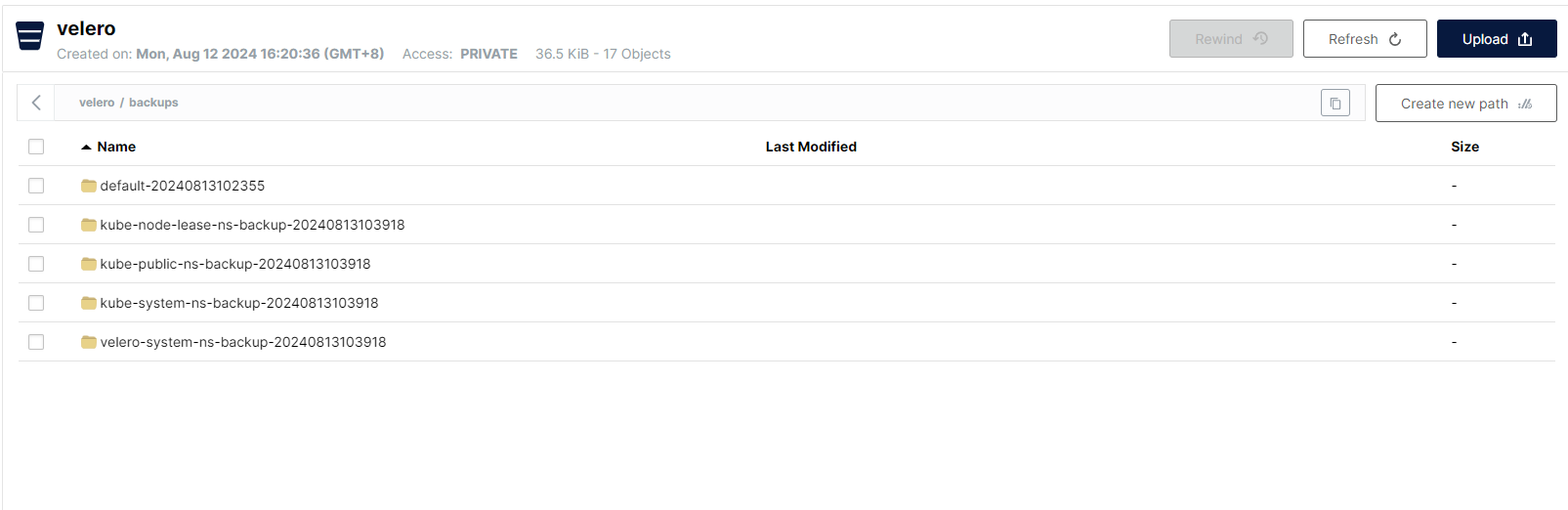
Velero 快速上手:使用 Velero 实现 Kubernetes 集群备份与迁移
一、veloro 简介
Velero 是vmware开源的一个云原生的灾难恢复和迁移工具,它本身也是开源的,采用Go语言编写,可以安全的备份、恢复和迁移Kubernetes集群资源数据;Velero 是西班牙语意思是帆船,非常符合Kubernetes社区的命名风格&a…
【Python快速入门和实践017】Python常用脚本-根据文件后缀对其进行分类保存
一、功能介绍 这段代码的功能是将源文件夹中的文件按照它们的文件扩展名分类并移动到不同的子文件夹中。步骤如下: 定义函数:move_files_by_extension函数接收两个参数: source_folder:源文件夹路径。destination_folderÿ…
LLM + GraphRAG技术,赋能教育培训行业数字化创新
随着人工智能大模型时代的到来,LLM大语言模型、RAG增强检索、Graph知识图谱、Prompt提示词工程等技术的发展日新月异,也让各行各业更加期待技术带来的产业变革。
比如,教育培训行业,教师数量相对有限、学生个体差异较大ÿ…
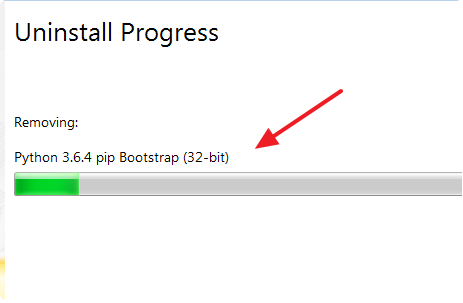
怎样卸载python
python卸载干净的具体操作步骤如下:
1、首先打开电脑左下角开始菜单,点击“运行”选项,输入“cmd”。 2、输入“python --version”,得到一个程序的版本,按回车键。 3、点击下图程序。 4、然后在该页面中点击“uninst…
【投融界-注册安全分析报告】
前言
由于网站注册入口容易被黑客攻击,存在如下安全问题:
暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…
8 自动类型转换、强制类型转换、整数数据溢出与模运算、浮点数精度丢失、类型转换值截断
目录
1 自动类型转换(隐式转换)
1.1 运算过程中的自动类型转换
1.1.1 转换规则
1.1.2 转换方向
1.1.3 案例演示
1.2 赋值时的自动类型转换
1.2.1 案例演示
2 强制类型转换(显式转换)
2.1 介绍
2.2 转换格式
2.3 转换规…
案例分享—国外毛玻璃效果UI设计案例
毛玻璃效果通过模糊和半透明特性,显著增强了UI界面的层次感和深度,使得元素之间界限清晰,同时赋予界面一种现代、高级的质感,提升了整体视觉吸引力。 该效果不仅美观,还通过柔和的色彩和光照效果营造出清新、轻松的氛围…
回归分析系列1-多元线性回归
03 多元线性回归
3.1 简介
多元线性回归是简单线性回归的扩展,允许我们同时研究多个自变量对因变量的影响。多元回归模型可以表示为: 其中,x1,x2,…,xp是 p 个自变量,β0 是截距,β1,β2,…,βp是对应的回归系数&…