题目链接: 01 矩阵

多源BFS类型题, 即给定多个起点, 判断从哪个起点走到终点距离最短, 一般解题思路为将所有起点看成一个"起点", 由此"起点"做bfs得到题解, 实际代码编写将所有起点都入队列, 每次都对所有起点做一层扩展.

题解思路:

从1往0处走寻找最短距离不好操作, 逆向思维从0往1处走, 这样很好更新最短距离, 如图:

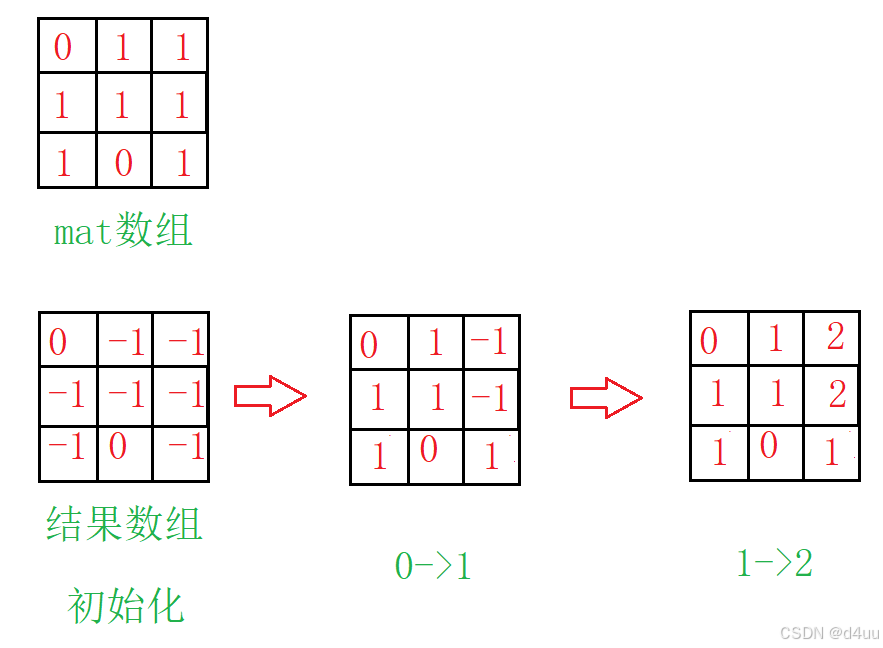
第一层的值为0, 那么扩展后的值就是0+1

第二层的值为1, 那么扩展后的值就是1+1

题解大致步骤:

1. 定义方向数组.

2. 定义一个与mat同等规模的二维数组, 将其初始值设为-1, 当数组对应坐标的值为-1时表示当前位置未被访问过, 当数组对应坐标的值不为-1时则表示该坐标到0的最短距离.

3. 定义一个存储pair<int,int>的队列, 并将mat数组中0的坐标入队, 同时将步骤2定义的数组的同等坐标位置的值置为0.

4. 做一次多源bfs, 每次取队头的值向四周扩一次, 并根据条件更新队列和步骤2的数组, 最后步骤2的数组就是题解, 返回即可.

题解代码:

class Solution 
{
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) 
    {
        //方向数组
        int dx[4] = {0, 0, -1, 1};
        int dy[4] = {1, -1, 0, 0};

        int row = mat.size();
        int col = mat[0].size();
        vector<vector<int>> res(row, vector<int>(col, -1));
        queue<pair<int,int>> q;

        //添加0的坐标到q
        for(int i = 0; i < row; ++i)
        {
            for(int j = 0; j < col; ++j)
            {
                if(mat[i][j] == 0)
                {
                    q.push({i, j});
                    res[i][j] = 0; //同时修改结果数组
                }
            }
        }

        //多源bfs
        while(q.size())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int j = 0; j < 4; ++j)
            {
                int x = a + dx[j];
                int y = b + dy[j];
                if(x >= 0 && x < row && y >= 0 && y < col && res[x][y] == -1)
                {
                    q.push({x, y});
                    res[x][y] = res[a][b] + 1;
                }
            }
        }

        return res;
    }
};