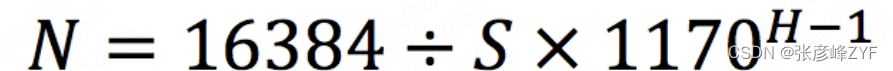前言
本篇博客讲解c++STL中的stack/queue
💓 个人主页：普通young man-CSDN博客
⏩ 文章专栏：C++_普通young man的博客-CSDN博客
⏩ 本人giee: 普通小青年 (pu-tong-young-man) - Gitee.com
若有问题 评论区见📝
🎉欢迎大家点赞👍收藏⭐文章
目录
stack的介绍
1. 栈概述
2. 栈实现
3. 底层容器的要求
4. 标准容器的选择
stack的使用
stack的实现：
queue的介绍
编辑
1. 队列概述
2. 队列实现
3. 底层容器的要求
4. 标准容器的选择
queue的使用
queue的实现
priority_queue的介绍
优先级队列概述
2. 底层容器
3. 堆算法
4. 优先级队列与堆的关系
5. 默认情况下是大堆
priority_queue的实现
仿函数
什么是仿函数？
仿函数的特点
仿函数的例子
仿函数的应用场景
容器适配器
适配器模式定义
deque的简单介绍(了解)
基本概念
内部实现
片段管理
插入和删除
deque的缺点
与std::vector比较
与std::list比较
实际应用场景
为什么选择deque作为stack和queue的底层默认容器
为什么选择 std::deque 作为 std::stack 和 std::queue 的底层容器
这篇博客讲解stack和queue的使用和底层原理
由于栈和队列都在C语言的时候学过，所以我就不卖关子了
stack的介绍
stack - C++ Reference (cplusplus.com)
https://legacy.cplusplus.com/reference/stack/stack/
1. 栈概述
栈是一种容器适配器，专门用于在 LIFO（后进先出）上下文中操作。在这种上下文中，元素从容器的一端插入（压栈），也是从同一端提取（弹栈）。
2. 栈实现
栈作为容器适配器实现，它封装了一个特定的容器类作为其底层容器类，并提供了一组特定的成员函数来访问其元素。元素总是从栈的顶部压入和弹出。
3. 底层容器的要求
底层容器可以是标准容器类模板之一，也可以是其他专门设计的容器类。该底层容器应至少支持以下操作：
empty(): 检测栈是否为空。size(): 返回栈中有效元素的个数。top(): 返回栈顶元素的引用。push(): 在栈顶压入一个新元素。pop(): 从栈顶弹出一个元素。4. 标准容器的选择
标准容器类
deque和vector满足这些要求。默认情况下，如果没有为stack实例化指定容器类，则使用标准容器deque作为底层容器。
总结来说，栈是一种容器适配器，用于处理后进先出的数据。它使用一个底层容器类来存储数据，并提供了一组特定的接口来操作这些数据。底层容器必须支持基本的栈操作，如检测是否为空、获取元素数量、获取栈顶元素以及压栈和弹栈操作。标准的
deque和vector类可以作为底层容器使用，其中deque是默认选择。
stack的使用
| 方法名称 | 描述 |
|---|---|
stack() | 构造一个空的栈。 |
empty() | 检查栈是否为空；如果是空栈返回 true，否则返回 false。 |
size() | 返回栈中元素的数量。 |
top() | 返回栈顶元素的引用，但不移除该元素。 |
push(val) | 将元素 val 添加到栈的顶部。 |
pop() | 移除栈顶的元素，并返回被移除的元素。 |
这边直接做几个题目来熟悉这个stack
栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)https://www.nowcoder.com/practice/d77d11405cc7470d82554cb392585106?tpId=13&&tqId=11174&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking
#include <cstddef>
#include <stack>
class Solution {
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
size_t i = 0;
std::stack<int> v; // 创建一个栈 v 用于存储 pushV 中的元素
for (auto& it : pushV) { // 遍历 pushV 中的每一个元素
v.push(it); // 将当前元素 it 压入栈 v 中
// 当栈不为空且栈顶元素等于 popV 中当前应弹出的元素时
while (!v.empty() && v.top() == popV[i]) {
v.pop(); // 弹出栈顶元素
++i; // 移动到 popV 的下一个元素
}
}
// 如果栈 v 在遍历完 pushV 后为空，则说明所有的 push 和 pop 操作都符合栈的规则
return v.empty();
}
};
初始化:
size_t i = 0;: 初始化一个索引i用于追踪popV中当前应该弹出的元素的位置。std::stack<int> v;: 创建一个整型栈v用于存储pushV中的元素。遍历并压栈:
for (auto& it : pushV) { ... }: 遍历pushV中的每一个元素it。v.push(it);: 将当前元素it压入栈v中。匹配弹出:
while (!v.empty() && v.top() == popV[i]) { ... }: 只要栈v不为空并且栈顶元素等于popV中当前位置i的元素，则执行循环。v.pop();: 弹出栈顶元素。++i;: 将索引i加一，指向popV中的下一个元素。结果返回:
return v.empty();: 如果栈v在遍历完pushV后为空，则说明所有的 push 和 pop 操作都符合栈的规则，返回true；否则返回false。示例用法：
假设我们有如下输入：
pushV = [1, 2, 3, 4, 5]popV = [4, 5, 3, 2, 1]该函数将返回
true，因为可以通过这样的操作序列来实现：
- 将 1、2、3、4、5 依次压入栈中。
- 从栈中依次弹出 4、5、3、2、1。
如果
popV为[4, 3, 5, 1, 2]，则函数将返回false，因为无法通过合法的 push 和 pop 操作得到这样的序列。
155. 最小栈 - 力扣（LeetCode）https://leetcode.cn/problems/min-stack/description/
class MinStack {
public:
MinStack() {}
void push(int val) {
//
_st.push(val);
// 如果val小于min中的值就压栈
if (_min.empty() || val <= _min.top()) {
_min.push(val);
}
}
void pop() {
// 如果栈顶元素是一样的——mid也需要pop，因为这个数据已经要被pop，不在了
if (_st.top() == _min.top()) {
_min.pop();
}
_st.pop();
}
int top() { return _st.top(); }
int getMin() { return _min.top(); }
private:
// 定义两个栈（一个正常压栈，一个存储最小的值）
stack<int> _st;
stack<int> _min;
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/
push(val): 将val压入栈中，并维护一个额外的栈_min来跟踪当前栈中的最小值。pop(): 从栈中弹出顶部元素，并同步更新_min。top(): 返回栈顶元素。getMin(): 返回当前栈中的最小值。成员函数解释
push(val)
- 将
val压入_st。- 如果
_min为空或val小于等于_min的栈顶元素，则将val压入_min。
pop()
- 如果
_st和_min的栈顶元素相同，则弹出_min的栈顶元素。- 弹出
_st的栈顶元素。
top()
- 返回
_st栈顶的元素。
getMin()
- 返回
_min栈顶的元素，即当前栈中的最小值。push(val): 将val压入栈中，并维护一个额外的栈_min来跟踪当前栈中的最小值。pop(): 从栈中弹出顶部元素，并同步更新_min。top(): 返回栈顶元素。getMin(): 返回当前栈中的最小值。成员函数解释
push(val)
- 将
val压入_st。- 如果
_min为空或val小于等于_min的栈顶元素，则将val压入_min。
pop()
- 如果
_st和_min的栈顶元素相同，则弹出_min的栈顶元素。- 弹出
_st的栈顶元素。
top()
- 返回
_st栈顶的元素。
getMin()
- 返回
_min栈顶的元素，即当前栈中的最小值。
232. 用栈实现队列 - 力扣（LeetCode）https://leetcode.cn/problems/implement-queue-using-stacks/description/
class MyQueue {
public:
MyQueue() {}
void push(int x) { s1.push(x); }
int pop() {
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
}
int ret = s2.top();
s2.pop();
return ret;
}
int peek() {
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
}
return s2.top();
}
bool empty() { return s1.empty() && s2.empty(); }
private:
stack<int> s1;
stack<int> s2;
};
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue* obj = new MyQueue();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->peek();
* bool param_4 = obj->empty();
*/
push(x): 将x压入s1。pop(): 从s2弹出栈顶元素（如果s2为空，则先将s1中的元素全部转移到s2）。peek(): 返回s2的栈顶元素（如果s2为空，则先将s1中的元素全部转移到s2）。empty(): 检查s1和s2是否都为空。成员函数解释
push(x)
- 将
x压入s1。
pop()
- 如果
s2为空，将s1中的所有元素转移到s2。- 从
s2中弹出并返回栈顶元素。
peek()
- 如果
s2为空，将s1中的所有元素转移到s2。- 返回
s2的栈顶元素。
empty()
- 如果
s1和s2都为空，则返回true；否则返回false。
stack的实现：
#pragma once
#include<vector>
#include<list>
#include<deque>
#include<iostream>
using namespace std;
namespace yang {
template<class T,class Container = deque<T>>
class stack
{
public:
void push(const T& val) {
_con.push_back(val);
}
void pop() {
_con.pop_back();
}
size_t size() const{
return _con.size();
}
size_t top() {
return _con.back();
}
bool empty() {
return _con.empty();
}
private:
Container _con;
};
void test1() {
stack<int> s1;
s1.push(1);
s1.push(1);
s1.push(1);
s1.push(1);
while (!s1.empty())
{
cout << s1.top() << " ";
s1.pop();
}
}
}
queue的介绍
queue - C++ Reference (cplusplus.com)https://legacy.cplusplus.com/reference/queue/queue/
1. 队列概述
队列是一种容器适配器，专门用于在 FIFO（先进先出）上下文中操作。在这种上下文中，元素从容器的一端插入（入队），从另一端提取（出队）。
2. 队列实现
队列作为容器适配器实现，它封装了一个特定的容器类作为其底层容器类，并提供了一组特定的成员函数来访问其元素。元素从队列的尾部入队（即添加到队列末尾），从队列的头部出队（即从队列前端移除）。
3. 底层容器的要求
底层容器可以是标准容器类模板之一，也可以是其他专门设计的容器类。该底层容器应至少支持以下操作：
empty(): 检测队列是否为空。size(): 返回队列中有效元素的个数。front(): 返回队头元素的引用。back(): 返回队尾元素的引用。push_back(): 在队列尾部入队列。pop_front(): 在队列头部出队列。4. 标准容器的选择
标准容器类
deque和list满足这些要求。默认情况下，如果没有为queue实例化指定容器类，则使用标准容器deque作为底层容器。
总结来说，队列是一种容器适配器，用于处理先进先出的数据。它使用一个底层容器类来存储数据，并提供了一组特定的接口来操作这些数据。底层容器必须支持基本的队列操作，如检测是否为空、获取元素数量、获取队头和队尾元素以及入队和出队操作。标准的
deque和list类可以作为底层容器使用，其中deque是默认选择。
queue的使用
| 方法名称 | 描述 |
|---|---|
queue() | 构造一个空的队列。 |
empty() | 检查队列是否为空；如果是空队列返回 true，否则返回 false。 |
size() | 返回队列中有效元素的数量。 |
front() | 返回队头元素的引用，但不移除该元素。 |
back() | 返回队尾元素的引用，但不移除该元素。 |
push(val) | 在队尾将元素 val 入队列。 |
pop() | 将队头元素出队列。 |
还是一样的我们做几道题
225. 用队列实现栈 - 力扣（LeetCode）https://leetcode.cn/problems/implement-stack-using-queues/
#include <queue>
class MyStack {
public:
MyStack() {}
// 将元素 x 压入栈中
void push(int x) {
s2.push(x); // 将新元素压入 s2
while (!s1.empty()) { // 将 s1 中的所有元素依次弹出并压入 s2
s2.push(s1.front());
s1.pop();
}
swap(s1, s2); // 交换 s1 和 s2，使得 s1 成为主队列
}
// 从栈中弹出并返回栈顶元素
int pop() {
int ret = s1.front(); // 获取栈顶元素
s1.pop(); // 弹出栈顶元素
return ret; // 返回弹出的元素
}
// 返回栈顶元素的引用，但不弹出
int top() { return s1.front(); }
// 检查栈是否为空
bool empty() { return s1.empty() && s2.empty(); }
private:
std::queue<int> s1; // 主队列，用于存储栈中的元素
std::queue<int> s2; // 辅助队列，用于临时存储元素
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
构造函数
MyStack():
- 初始化
MyStack对象。函数
void push(int x):
- 将新元素
x压入s2。- 将
s1中的所有元素依次弹出并压入s2，这样可以反转元素的顺序，使得s2的队尾元素成为栈的栈顶元素。- 交换
s1和s2，使s1成为主队列。函数
int pop():
- 从
s1中弹出并返回栈顶元素。函数
int top():
- 返回
s1的队头元素，即栈顶元素。函数
bool empty():
- 检查
s1和s2是否都为空，如果两者都为空，则返回true表示栈为空；否则返回false。
102. 二叉树的层序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-level-order-traversal/description/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret; // 用于存储层次遍历的结果
queue<TreeNode*> q; // 用于暂存每一层的节点
int Size = 0; // 当前层的节点数
if (root) {
q.push(root); // 将根节点入队
Size = q.size(); // 更新当前层的节点数
}
while (!q.empty()) {
vector<int> tmp; // 用于存储当前层的数据
// 处理当前层的所有节点
while (Size--) {
TreeNode* front = q.front(); // 获取队列前端的节点
q.pop(); // 从队列中弹出节点
tmp.push_back(front->val); // 将节点值添加到 tmp 中
// 将左右子节点入队
if (front->left)
q.push(front->left);
if (front->right)
q.push(front->right);
}
// 将当前层的数据添加到结果中
ret.push_back(tmp);
// 更新下一层的节点数
Size = q.size();
}
// 返回层次遍历的结果
return ret;
}
};
初始化:
vector<vector<int>> ret;: 初始化一个二维向量ret用于存储层次遍历的结果。queue<TreeNode*> q;: 初始化一个队列q用于暂存每一层的节点。int Size = 0;: 初始化一个变量Size用于记录当前层的节点数。处理根节点:
- 如果
root不为空，则将其入队，并更新Size。层次遍历:
while (!q.empty()): 当队列不为空时，持续处理。vector<int> tmp;: 用于存储当前层的数据。while (Size--): 处理当前层的所有节点。TreeNode* front = q.front();: 获取队列前端的节点。q.pop();: 从队列中弹出节点。tmp.push_back(front->val);: 将节点值添加到tmp中。if (front->left) q.push(front->left);: 如果节点有左子节点，则将其入队。if (front->right) q.push(front->right);: 如果节点有右子节点，则将其入队。ret.push_back(tmp);: 将当前层的数据添加到结果中。Size = q.size();: 更新下一层的节点数。返回结果:
return ret;: 返回层次遍历的结果。
queue的实现
#pragma once
#include<vector>
#include<list>
#include<deque>
#include<iostream>
namespace yang {
template <class T,class container = deque<T>>
class queue
{
public:
void push(const T& val) {
_con.push_back(val);
}
void pop() {
_con.pop_front();
}
bool empty() {
return _con.empty();
}
size_t size()const {
_con.size();
}
const T& front() const{
return _con.front();
}
const T& back()const {
return _con.back();
}
private:
container _con;
};
void test8() {
queue<int> s1;
s1.push(1);
s1.push(2);
s1.push(3);
s1.push(4);
while (!s1.empty())
{
cout << s1.front() << " ";
s1.pop();
}
}
}priority_queue的介绍
priority_queue - C++ Referencehttps://legacy.cplusplus.com/reference/queue/priority_queue
1. 元素类型 T
- 类型 T：这是
std::priority_queue中元素的数据类型。例如，你可以使用整数int或者自定义的类类型。2. 比较器 Compare
- 比较器 Compare：这是一个可调用的对象类型，用于确定优先队列中元素的顺序。通常情况下，你可以使用
std::less<T>或std::greater<T>，或者自定义一个函数对象。
优先级队列概述
优先级队列是一种特殊的队列，其中元素按照一定的优先级顺序排列。在默认情况下，优先级队列使用最大堆（大顶堆）来实现，这意味着队列中的最大元素位于队列的前端。
2. 底层容器
优先级队列默认使用
vector作为其底层存储数据的容器。vector提供了随机访问的能力，这对于构建和维护堆结构非常重要。3. 堆算法
在
vector上使用了堆算法将vector中的元素构造成堆的结构。堆是一种特殊的完全二叉树，其中每个父节点的值都不小于（对于最大堆）或不大于（对于最小堆）其子节点的值。4. 优先级队列与堆的关系
由于优先级队列默认使用最大堆实现，因此可以说
priority_queue就是一个堆。这意味着所有需要用到堆的地方都可以考虑使用priority_queue。5. 默认情况下是大堆
在默认情况下，
priority_queue实现的是最大堆，即队列的顶部元素是所有元素中的最大值。如果需要实现最小堆，可以通过传递一个自定义比较器来改变排序规则。
| 方法名称 | 描述 |
|---|---|
priority_queue() | 构造一个空的优先级队列。 |
priority_queue(first, last) | 构造一个优先级队列，使用迭代器范围 [first, last) 初始化队列。 |
empty() | 检查优先级队列是否为空；如果是空队列返回 true，否则返回 false。 |
top() | 返回优先级队列中的最大（或最小）元素，即堆顶元素。 |
push(x) | 在优先级队列中插入元素 x。 |
pop() | 删除优先级队列中的最大（或最小）元素，即堆顶元素。 |
还是一道题
215. 数组中的第K个最大元素 - 力扣（LeetCode）https://leetcode.cn/problems/kth-largest-element-in-an-array/
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int> s1(nums.begin(), nums.end());
for (int i = 0; i < k - 1; i++) {
s1.pop();
}
return s1.top();
}
};priority_queue的实现
#pragma once
#include<vector>
//比较
//大堆
template<class T>
class Less {
public:
//仿函数
bool operator()(const T& x, const T& y) {
return x < y;
}
};
//小堆
template<class T>
class Greater {
public:
//仿函数
bool operator()(const T& x, const T& y) {
return x > y;
}
};
namespace yang {
template<class T, class Container = vector<T>, class Conpear = Less<T>>
class priority_queue
{
public:
//向上调整建堆
void Adjustup(int child) {
//仿函数
Conpear con;//比较(升序/降序)
int parent = (child - 1) / 2;
while (child > 0)//到1下标就是最后位置，因为0下标计算parent越界
{
if (con(_con[parent], _con[child])) {
swap(_con[parent], _con[child]);
child = parent;
int parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void push(const T& val) {
_con.push_back(val);
Adjustup(_con.size() - 1);
}
//向下调整建堆
void Anjustdown(int parent) {
//仿函数
Conpear con;//比较(升序/降序)
int child = parent * 2 + 1;//左孩子
while (child < _con.size())
{
//判断左孩子和右孩子(大/小)
if (child + 1 < _con.size() && con(_con[child], _con[child + 1]))
{
child++;
}
if (con(_con[parent], _con[child])) {
swap(_con[parent], _con[child]);
child = parent;
int child = parent * 2 + 1;//左孩子
}
else
{
break;
}
}
}
void pop() {
//交换头尾
swap(_con[0], _con[_con.size() - 1]);
//删除尾部
_con.pop_back();
Anjustdown(0);
}
const T& top() {
return _con[0];
}
bool empty() const {
return _con.empty();
}
size_t size()const {
return _con.size();
}
private:
Container _con;
};
void test1() {
//priority_queue<int> a1;
priority_queue<int,vector<int>,Greater<int>> a1;
a1.push(1);
a1.push(5);
a1.push(0);
while (!a1.empty())
{
cout << a1.top() << " ";
a1.pop();
}
}
}
仿函数
什么是仿函数？
仿函数是一种特殊类型的类，它重载了函数调用运算符
operator()。这意味着你可以像调用普通函数那样调用这类对象，即使它们实际上是一个类的实例。这种技术在C++中非常有用，因为它允许你将函数式编程的概念与面向对象编程相结合。仿函数的特点
- 封装性:
- 仿函数可以封装状态（即数据成员）和行为（即成员函数），这使得它们可以拥有自己的状态并执行复杂的操作。
- 灵活性:
- 仿函数可以接受参数，并根据需要执行不同的操作。它们可以有多个版本，以适应不同的情况。
- 可扩展性:
- 仿函数可以很容易地扩展其功能，只需添加更多的成员函数或数据成员即可。
- 重用性:
- 由于仿函数可以被多次调用，因此可以在多个地方重用同一个仿函数对象。
- 通用性:
- 仿函数可以作为模板参数或泛型算法的参数使用，这增加了它们的通用性和适用范围。
仿函数的例子
下面是一个简单的仿函数示例，该仿函数用于计算两个整数的和：
#include <iostream>
// 定义一个仿函数类
struct Adder {
// 重载函数调用运算符
int operator()(int a, int b) const {
return a + b;
}
};
int main() {
Adder adder; // 创建仿函数对象
int result = adder(5, 3); // 调用仿函数对象
std::cout << "Result: " << result << std::endl; // 输出 Result: 8
return 0;
}仿函数的应用场景
- 泛型算法:
- 仿函数经常作为泛型算法（如
std::sort,std::find_if）的参数使用，以定制算法的行为。- 多态:
- 仿函数可以用于实现多态行为，尤其是在没有虚函数的情况下。
- 事件处理:
- 仿函数可以用于事件驱动的编程模型中，作为事件处理器。
- 回调函数:
- 仿函数可以用作回调函数，以响应特定事件或条件。
这边我写一个日期类
class Date
{
public:
Date(int year = 1900, int month = 1, int day = 1)
: _year(year)
, _month(month)
, _day(day)
{}
bool operator<(const Date& d)const
{
return (_year < d._year) ||
(_year == d._year && _month < d._month) ||
(_year == d._year && _month == d._month && _day < d._day);
}
bool operator>(const Date& d)const
{
return (_year > d._year) ||
(_year == d._year && _month > d._month) ||
(_year == d._year && _month == d._month && _day > d._day);
}
friend ostream& operator<<(ostream& _cout, const Date& d)
{
_cout << d._year << "-" << d._month << "-" << d._day;
return _cout;
}
private:
int _year;
int _month;
int _day;
};
class DateLess
{
public:
bool operator()(Date* p1, Date* p2)
{
return *p1 < *p2;
}
};
然后我先运行这段测试
这个没什么毛病
下面我加一段测试
这段代码运行三次的结果：
你会发现三次结果都不一样，为什么?
其实这是因为他们传的地址，其实也是比较的地址，库里的仿函数，不支持这样弄，所以需要自己写一个:
这里我们可以给出一个总结：
仿函数：本质是一个类，这个类重载operator(),他的对象可以像函数一样使用
注意：
1、类类型不支持比较大小
2、支持比较大小，但是比较的逻辑不是你想要的 需要自己实现仿函数
容器适配器
适配器模式定义
适配器模式是一种结构型设计模式，它允许你不改变现有类的接口，而是通过创建一个新的类来“包裹”原有的类，从而达到转换接口的目的。适配器模式使得原本不兼容的接口可以一起工作。
容器适配器是一种特殊的容器，它们不是直接存储数据，而是提供了一种特定的接口来访问底层容器中的数据。
stack和queue都是容器适配器，它们基于其他容器类来实现特定的数据访问模式。
deque的简单介绍(了解)
这个咋理解？其实他是一个list和vector的结合体，大家可以去看一本书《STL源码刨析》这里面有很详细的介绍
deque - C++ Reference (cplusplus.com)https://legacy.cplusplus.com/reference/deque/deque/
这个容器综合了这两个容器，我们看一下他的一个结构
deque并不是真正连续的空间，而是由一段段连续的小空间拼接而成的，实际deque类似于一个 动态的二维数组，其底层结构如下图所示：
双端队列底层是一段假象的连续空间，实际是分段连续的，为了维护其“整体连续”以及随机访问 的假象，落在了deque的迭代器身上，因此deque的迭代器设计就比较复杂，如下图所示：
这些都可以在那本书上看到
基本概念
std::deque是一个序列容器，它提供了一种动态数组的抽象，并且可以在其头部或尾部高效地添加或删除元素。与std::vector不同的是，std::deque在内部使用了更加复杂的数据结构来实现这种功能，从而避免了重新分配内存所带来的性能开销。内部实现
std::deque的内部实现通常基于分段存储的方式。它将数据分成多个连续的块来存储，每个块称为一个“缓冲区”或者“片段”。每个片段都是一段连续的内存空间，这样在片段内部可以快速随机访问。而片段之间则是通过指针链接起来的，形成一个链表结构。片段管理
- 片段大小：为了减少内存碎片和提高内存利用率，deque会根据需要动态调整每个片段的大小。一般情况下，deque会在创建时设置一个初始片段大小，并随着容器的增长按一定比例增加片段大小。
- 控制结构：deque使用了一个控制结构来管理这些片段，这个控制结构本身通常是一个数组，其中每个元素对应一个片段，包含了指向该片段起始位置的指针，以及一些额外的信息如片段的实际大小等。
插入和删除
- 插入：当向deque的两端插入元素时，如果对应片段还有空闲空间，则直接插入；否则，创建一个新的片段并插入元素，同时更新控制结构。
- 删除：当从deque的两端删除元素时，只需简单地调整对应片段的边界即可。如果某个片段中的元素数量过少，则可能会合并相邻片段以释放内存。
deque的缺点
遍历效率较低：
std::deque由于其内部是由多个连续的小段内存组成的，所以在遍历过程中，迭代器需要跨越不同的内存段。这意味着迭代器不仅需要维护当前元素的位置信息，还需要跟踪当前所处的内存段以及该段内的偏移量。这种额外的检查和管理增加了遍历的成本。- 当迭代器从一个内存段移动到另一个内存段时，需要进行额外的操作，比如更新迭代器的内部状态，这可能导致遍历速度比
std::vector慢。内存管理复杂：
std::deque需要维护一个复杂的内存管理机制，包括控制结构（通常是数组）来追踪内存段的位置、大小等信息。这种机制虽然有助于提高插入和删除的效率，但同时也增加了实现的复杂性和潜在的错误风险。- 内存分配和释放的策略也较为复杂，例如在调整片段大小或合并片段时，需要更精细的控制。
与
std::vector比较
头部插入/删除：
std::deque在头部插入和删除元素时不需要移动其他元素，因此效率非常高。std::vector在头部插入或删除元素时需要移动所有后续元素，这在元素较多时会导致较高的成本。扩容效率：
std::deque在扩容时，只需要添加新的内存段，不需要像std::vector那样可能需要复制整个数组到新的内存区域，因此在处理大量数据时，std::deque的扩容更为高效。与
std::list比较
- 内存利用率：
std::deque的内存使用更为紧凑，因为它的元素存储在连续的内存中，不需要为每个元素存储额外的指针信息。std::list则需要为每个元素维护前后指针，这会占用额外的空间。实际应用场景
- 由于上述特点，
std::deque在需要频繁进行头部插入和删除操作的场景下非常有用，而在需要频繁遍历的场景下则不如std::vector或std::list合适。- 在实际应用中，
std::deque常常被用于实现需要高效两端操作的容器，例如std::stack和std::queue的某些实现可能会使用std::deque作为底层数据结构，特别是在需要支持从两端弹出元素的队列实现中。这边我用一个排序来比较一下
//比较deque的效率 void test_op1() { srand(time(0)); const int N = 1000000; deque<int> dq1; vector<int> dq2; for (int i = 0; i < N; ++i) { auto e = rand() + i; dq1.push_back(e); dq2.push_back(e); } int begin1 = clock(); sort(dq1.begin(), dq1.end()); int end1 = clock(); int begin2 = clock(); sort(dq2.begin(), dq2.end()); int end2 = clock(); printf("deque sort:%d\n", end1 - begin1); printf("vector sort:%d\n", end2 - begin2); } void test_op2() { srand(time(0)); const int N = 1000000; deque<int> dq1; deque<int> dq2; for (int i = 0; i < N; ++i) { auto e = rand() + i; dq1.push_back(e); dq2.push_back(e); } int begin1 = clock(); sort(dq1.begin(), dq1.end()); int end1 = clock(); int begin2 = clock(); // 拷贝到vector vector<int> v(dq2.begin(), dq2.end()); sort(v.begin(), v.end()); dq2.assign(v.begin(), v.end()); int end2 = clock(); printf("deque sort:%d\n", end1 - begin1); printf("deque copy vector sort, copy back deque:%d\n", end2 - begin2); }
我们可以看到vector确实在效率上高于deque
为什么选择deque作为stack和queue的底层默认容器
为什么选择 std::deque 作为 std::stack 和 std::queue 的底层容器
主要他是list，vector的综合
高效插入和删除:
std::deque支持在两端高效地插入和删除元素。对于栈来说，这意味着可以在栈顶（通常是容器的尾部）进行快速的压栈和弹栈操作；对于队列来说，可以在队首（通常是容器的头部）进行快速的出队操作，在队尾进行快速的入队操作。- 相比之下，
std::vector在头部插入或删除元素时需要移动大量元素，效率较低；而std::list虽然也可以在两端进行高效操作，但它需要额外的指针来维护元素之间的链接，这会消耗更多的内存。内存管理:
std::deque的内存管理机制允许它在扩展时仅需分配新的内存段，而不是重新分配整个数组，这使得它在扩容时更为高效。- 对于栈和队列这样的数据结构来说，它们往往需要频繁地添加和删除元素，使用
std::deque可以减少内存重分配带来的开销。内存布局:
std::deque的元素存储在连续的内存中（尽管是在多个内存段中），这有利于缓存友好性，从而提高访问速度。std::deque的这种布局方式也意味着它在遍历数据时比std::list更加高效，尽管与std::vector相比遍历效率略低，但在栈和队列中，遍历的需求相对较少。泛用性:
std::deque提供了广泛的操作接口，可以方便地支持栈和队列所需的大部分操作，如push_back,pop_back,push_front,pop_front等。- 这使得
std::deque成为一个通用的选择，可以灵活地适应不同类型的容器需求。
