第九章 动态规划part07
今天就是打家劫舍的一天,这个系列不算难,大家可以一口气拿下。
198.打家劫舍
视频讲解:https://www.bilibili.com/video/BV1Te411N7SX
https://programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html
213.打家劫舍II
视频讲解:https://www.bilibili.com/video/BV1oM411B7xq
https://programmercarl.com/0213.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8DII.html
337.打家劫舍III
视频讲解:https://www.bilibili.com/video/BV1H24y1Q7sY
https://programmercarl.com/0337.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8DIII.html
198.打家劫舍
题目链接
https://leetcode.cn/problems/house-robber/description/
解题思路
经典dp问题
当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。
所以这里就更感觉到,当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式。
1.确定dp数组以及下标的含义
dp[i]:下标i以及i之前的房屋,最多可以偷窃的金额是dp[i]
2.确定递推公式
这里就是偷不偷i 偷:dp[i-2]+nums[i] 不偷:dp[i-1] 取最大值
dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
3.如何初始化dp数组
根据递推公式是dp[i-2] dp[i-1] 那么一定要初始化dp[0]和dp[1]
dp[0]一定是nums[0]
从dp[i]的定义上来讲 如果只有0 1 dp[1] 就是取nums[0]和nums[1] 的最大值
可以自己举例 数组{0,1} {0 ,1,2} {0 ,1,2,3}
4.确定遍历顺序 dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历
5.打印dp数组
code
class Solution {
public int rob(int[] nums) {
if(nums.length==0){
return 0;
}
if(nums.length==1){
return nums[0];
}
int[] dp=new int[nums.length];
dp[0]=nums[0];
dp[1]=Math.max(nums[0],nums[1]);
for(int i=2;i<nums.length;i++){
dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[nums.length-1];
}
}
213.打家劫舍II
题目链接
https://leetcode.cn/problems/house-robber-ii/description/
解题思路
情况一:考虑不包含首尾元素
情况二:考虑包含首元素,不包含尾元素
情况三:考虑包含尾元素,不包含首元素
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了
省下就是抽离打家劫舍I的代码 调用 取最大值就可以了。
code
class Solution {
public int rob(int[] nums) {
if(nums.length==0){
return 0;
}
if(nums.length==1){
return nums[0];
}
int res1=robRange(nums,1,nums.length-1);
int res2=robRange(nums,0,nums.length-2);
return Math.max(res1,res2);
}
public int robRange(int[] nums,int start,int end){
if(start==end) return nums[start];
int[] dp=new int[nums.length];
dp[start]=nums[start];
dp[start+1]=Math.max(nums[start],nums[start+1]);
for(int i=start+2;i<=end;i++){
dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[end];
}
}
337. 打家劫舍 III
题目链接
https://leetcode.cn/problems/house-robber-iii/description/
解题思路
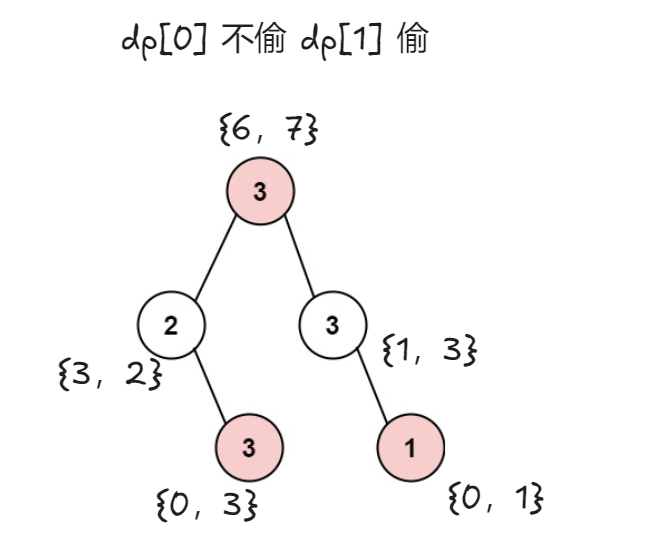
dp[i] 当前节点偷或不偷 只有俩个状态用dp[0]表示不偷dp[1]表示偷 的最大值
树形遍历一定是后序,因为要计算跟节点的值
递推公式就是
偷当前节点:当前节点的值+ 不偷左右孩子的值
不偷当前节点:左孩子偷或不偷的最大值 + 右孩子偷或不偷的最大值
最终就是后序遍历一层一层返回给跟节点计算出根结点偷或不偷的最大值
code
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
//树形dp dp[0] dp[1] 0是不偷 1是偷
//当前节点偷或者不偷 ,最后计算的是根节点使用后序遍历
public int rob(TreeNode root) {
int[] dp=robTree(root);
return Math.max(dp[0],dp[1]);
}
public int[] robTree(TreeNode node){
if(node==null){
return new int[]{0,0};
}
int[] leftDp=robTree(node.left);
int[] rightDp=robTree(node.right);
//偷当前节点 当前节点的值+不偷左右节点的值
int val0=node.val+leftDp[0]+rightDp[0];
//不偷当前节点,取left的偷和不偷的最大值 + 取right偷和不偷的最大值
int vla1=Math.max(leftDp[0],leftDp[1])+Math.max(rightDp[0],rightDp[1]);
return new int[]{vla1,val0};
}
}
树形dp状态图 :