pytorch 3 计算图

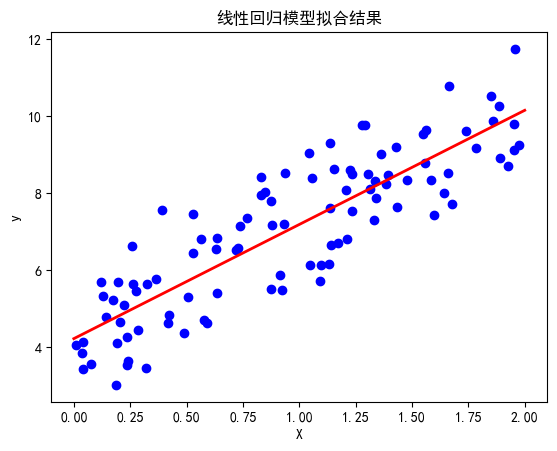
计算图结构

**加粗样式**

分析：

起始节点 a
b = 5 - 3a
c = 2b + 3
d = 5b + 6
e = 7c + d^2
f = 2e
最终输出 g = 3f - o（其中 o 是另一个输入）

前向传播

前向传播按照上述顺序计算每个节点的值。

反向传播过程

反向传播的目标是计算损失函数（这里假设为 g）对每个中间变量和输入的偏导数。从右向左进行计算：

∂g/∂o = -1
∂g/∂f = 3
∂f/∂e = 2
∂e/∂c = 7
∂e/∂d = 2d
∂d/∂b = 5
∂c/∂b = 2
∂b/∂a = -3

链式法则应用

使用链式法则计算出 g 对每个变量的全导数：

dg/df = ∂g/∂f = 3
dg/de = (∂g/∂f) * (∂f/∂e) = 3 * 2 = 6
dg/dc = (dg/de) * (∂e/∂c) = 6 * 7 = 42
dg/dd = (dg/de) * (∂e/∂d) = 6 * 2d
dg/db = (dg/dc) * (∂c/∂b) + (dg/dd) * (∂d/∂b)
= 42 * 2 + 6 * 2d * 5
= 84 + 60d
dg/da = (dg/db) * (∂b/∂a)
= (84 + 60d) * (-3)
= -252 - 180d

最终梯度

最终得到 g 对输入 a 和 o 的梯度：

dg/da = -252 - 180d
dg/do = -1

代码实现

静态图

import math

class Node:
    """
    表示计算图中的一个节点。
    每个节点都可以存储一个值、梯度，并且知道如何计算前向传播和反向传播。
    """
    def __init__(self, value=None):
        self.value = value  # 节点的值
        self.gradient = 0   # 节点的梯度
        self.parents = []   # 父节点列表
        self.forward_fn = lambda: None  # 前向传播函数
        self.backward_fn = lambda: None  # 反向传播函数

    def __add__(self, other):
        """加法操作"""
        return self._create_binary_operation(other, lambda x, y: x + y, lambda: (1, 1))

    def __mul__(self, other):
        """乘法操作"""
        return self._create_binary_operation(other, lambda x, y: x * y, lambda: (other.value, self.value))

    def __sub__(self, other):
        """减法操作"""
        return self._create_binary_operation(other, lambda x, y: x - y, lambda: (1, -1))

    def __pow__(self, power):
        """幂运算"""
        result = Node()
        result.parents = [self]
        def forward():
            result.value = math.pow(self.value, power)
        def backward():
            self.gradient += power * math.pow(self.value, power-1) * result.gradient
        result.forward_fn = forward
        result.backward_fn = backward
        return result

    def _create_binary_operation(self, other, forward_op, gradient_op):
        """
        创建二元操作的辅助方法。
        用于简化加法、乘法和减法的实现。
        """
        result = Node()
        result.parents = [self, other]
        def forward():
            result.value = forward_op(self.value, other.value)
        def backward():
            grads = gradient_op()
            self.gradient += grads[0] * result.gradient
            other.gradient += grads[1] * result.gradient
        result.forward_fn = forward
        result.backward_fn = backward
        return result

def topological_sort(node):
    """
    对计算图进行拓扑排序。
    确保在前向和反向传播中按正确的顺序处理节点。
    """
    visited = set()
    topo_order = []
    def dfs(n):
        if n not in visited:
            visited.add(n)
            for parent in n.parents:
                dfs(parent)
            topo_order.append(n)
    dfs(node)
    return topo_order

# 构建计算图
a = Node(2)  # 假设a的初始值为2
o = Node(1)  # 假设o的初始值为1

# 按照给定的数学表达式构建计算图
b = Node(5) - a * Node(3)
c = b * Node(2) + Node(3)
d = b * Node(5) + Node(6)
e = c * Node(7) + d ** 2
f = e * Node(2)
g = f * Node(3) - o

# 前向传播
sorted_nodes = topological_sort(g)
for node in sorted_nodes:
    node.forward_fn()

# 反向传播
g.gradient = 1  # 设置输出节点的梯度为1
for node in reversed(sorted_nodes):
    node.backward_fn()

# 打印结果
print(f"g = {g.value}")
print(f"dg/da = {a.gradient}")
print(f"dg/do = {o.gradient}")

# 验证手动计算的结果
d_value = 5 * b.value + 6
expected_dg_da = -252 - 180 * d_value
print(f"Expected dg/da = {expected_dg_da}")
print(f"Difference: {abs(a.gradient - expected_dg_da)}")

动态图

import math

class Node:
    """
    表示计算图中的一个节点。
    实现了动态计算图的核心功能，包括前向计算和反向传播。
    """
    def __init__(self, value, children=(), op=''):
        self.value = value  # 节点的值
        self.grad = 0       # 节点的梯度
        self._backward = lambda: None  # 反向传播函数，默认为空操作
        self._prev = set(children)  # 前驱节点集合
        self._op = op  # 操作符，用于调试

    def __add__(self, other):
        """加法操作"""
        other = other if isinstance(other, Node) else Node(other)
        result = Node(self.value + other.value, (self, other), '+')
        def _backward():
            self.grad += result.grad
            other.grad += result.grad
        result._backward = _backward
        return result

    def __mul__(self, other):
        """乘法操作"""
        other = other if isinstance(other, Node) else Node(other)
        result = Node(self.value * other.value, (self, other), '*')
        def _backward():
            self.grad += other.value * result.grad
            other.grad += self.value * result.grad
        result._backward = _backward
        return result

    def __pow__(self, other):
        """幂运算"""
        assert isinstance(other, (int, float)), "only supporting int/float powers for now"
        result = Node(self.value ** other, (self,), f'**{other}')
        def _backward():
            self.grad += (other * self.value**(other-1)) * result.grad
        result._backward = _backward
        return result

    def __neg__(self):
        """取反操作"""
        return self * -1

    def __sub__(self, other):
        """减法操作"""
        return self + (-other)

    def __truediv__(self, other):
        """除法操作"""
        return self * other**-1

    def __radd__(self, other):
        """反向加法"""
        return self + other

    def __rmul__(self, other):
        """反向乘法"""
        return self * other

    def __rtruediv__(self, other):
        """反向除法"""
        return other * self**-1

    def tanh(self):
        """双曲正切函数"""
        x = self.value
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        result = Node(t, (self,), 'tanh')
        def _backward():
            self.grad += (1 - t**2) * result.grad
        result._backward = _backward
        return result

    def backward(self):
        """
        执行反向传播，计算梯度。
        使用拓扑排序确保正确的反向传播顺序。
        """
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)
        
        self.grad = 1  # 设置输出节点的梯度为1
        for node in reversed(topo):
            node._backward()  # 对每个节点执行反向传播

def main():
    """
    主函数，用于测试自动微分系统。
    构建一个计算图，执行反向传播，并验证结果。
    """
    # 构建计算图
    a = Node(2)
    o = Node(1)
    b = Node(5) - a * 3
    c = b * 2 + 3
    d = b * 5 + 6
    e = c * 7 + d ** 2
    f = e * 2
    g = f * 3 - o

    # 反向传播
    g.backward()

    # 打印结果
    print(f"g = {g.value}")
    print(f"dg/da = {a.grad}")
    print(f"dg/do = {o.grad}")

    # 验证手动计算的结果
    d_value = 5 * b.value + 6
    expected_dg_da = -252 - 180 * d_value
    print(f"Expected dg/da = {expected_dg_da}")
    print(f"Difference: {abs(a.grad - expected_dg_da)}")

if __name__ == "__main__":
    main()

解释:

Node 类代表计算图中的一个节点,包含值、梯度、父节点以及前向和反向传播函数。
重载的数学运算符 (__add__, __mul__, __sub__, __pow__) 允许直观地构建计算图。
_create_binary_operation 方法用于创建二元操作,简化了加法、乘法和减法的实现。
topological_sort 函数对计算图进行拓扑排序,确保正确的计算顺序。

import math

class Node:
    """
    表示计算图中的一个节点。
    实现了动态计算图的核心功能，包括前向计算和反向传播。
    """
    def __init__(self, value, children=(), op=''):
        self.value = value  # 节点的值
        self.grad = 0       # 节点的梯度
        self._backward = lambda: None  # 反向传播函数，默认为空操作
        self._prev = set(children)  # 前驱节点集合
        self._op = op  # 操作符，用于调试

    def __add__(self, other):
        """加法操作"""
        other = other if isinstance(other, Node) else Node(other)
        result = Node(self.value + other.value, (self, other), '+')
        def _backward():
            self.grad += result.grad
            other.grad += result.grad
        result._backward = _backward
        return result

    def __mul__(self, other):
        """乘法操作"""
        other = other if isinstance(other, Node) else Node(other)
        result = Node(self.value * other.value, (self, other), '*')
        def _backward():
            self.grad += other.value * result.grad
            other.grad += self.value * result.grad
        result._backward = _backward
        return result

    def __pow__(self, other):
        """幂运算"""
        assert isinstance(other, (int, float)), "only supporting int/float powers for now"
        result = Node(self.value ** other, (self,), f'**{other}')
        def _backward():
            self.grad += (other * self.value**(other-1)) * result.grad
        result._backward = _backward
        return result

    def __neg__(self):
        """取反操作"""
        return self * -1

    def __sub__(self, other):
        """减法操作"""
        return self + (-other)

    def __truediv__(self, other):
        """除法操作"""
        return self * other**-1

    def __radd__(self, other):
        """反向加法"""
        return self + other

    def __rmul__(self, other):
        """反向乘法"""
        return self * other

    def __rtruediv__(self, other):
        """反向除法"""
        return other * self**-1

    def tanh(self):
        """双曲正切函数"""
        x = self.value
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        result = Node(t, (self,), 'tanh')
        def _backward():
            self.grad += (1 - t**2) * result.grad
        result._backward = _backward
        return result

    def backward(self):
        """
        执行反向传播，计算梯度。
        使用拓扑排序确保正确的反向传播顺序。
        """
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)
        
        self.grad = 1  # 设置输出节点的梯度为1
        for node in reversed(topo):
            node._backward()  # 对每个节点执行反向传播

def main():
    """
    主函数，用于测试自动微分系统。
    构建一个计算图，执行反向传播，并验证结果。
    """
    # 构建计算图
    a = Node(2)
    o = Node(1)
    b = Node(5) - a * 3
    c = b * 2 + 3
    d = b * 5 + 6
    e = c * 7 + d ** 2
    f = e * 2
    g = f * 3 - o

    # 反向传播
    g.backward()

    # 打印结果
    print(f"g = {g.value}")
    print(f"dg/da = {a.grad}")
    print(f"dg/do = {o.grad}")

    # 验证手动计算的结果
    d_value = 5 * b.value + 6
    expected_dg_da = -252 - 180 * d_value
    print(f"Expected dg/da = {expected_dg_da}")
    print(f"Difference: {abs(a.grad - expected_dg_da)}")

if __name__ == "__main__":
    main()