嗨!今天我们来聊聊如何用Python构建一个简单的线性回归模型。这个过程就像给数据配对舞一样,让它们在舞池里找到最佳位置。准备好了吗?让我们开始吧!🚀
第一步:数据准备
首先,我们要准备一些数据。想象一下,数据就像舞池里的小球,一个叫X,一个叫Y。我们可以用Python生成一些模拟的小球,或者用现成的数据集。
第二步:模型建立
接下来,我们用线性回归模型来拟合这些小球。在Python的世界里,scikit-learn库就像一个聪明的舞教练,它的LinearRegression类能帮我们创建和训练模型。
第三步:结果展示
模型训练完成后,我们会看到模型的参数,也就是舞池的斜率和截距。然后,我们用这个模型来预测新小球的舞步,并以图形化的方式展示出来,这样我们就能直观地看到模型的效果。
现在,让我们用Python代码来演示这个过程。我会生成一些模拟的小球,然后用线性回归模型来拟合它们,最后展示拟合结果。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成模拟数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 创建并训练模型
model = LinearRegression()
model.fit(X, y)
# 模型参数
slope = model.coef_[0]
intercept = model.intercept_
# 使用模型进行预测
X_new = np.array([[0], [2]])
y_predict = model.predict(X_new)
# 绘制数据点和拟合线
plt.scatter(X, y, color='blue')
plt.plot(X_new, y_predict, color='red', linewidth=2)
plt.xlabel('X')
plt.ylabel('y')
plt.title('线性回归模型拟合结果')
plt.show()
(slope, intercept)
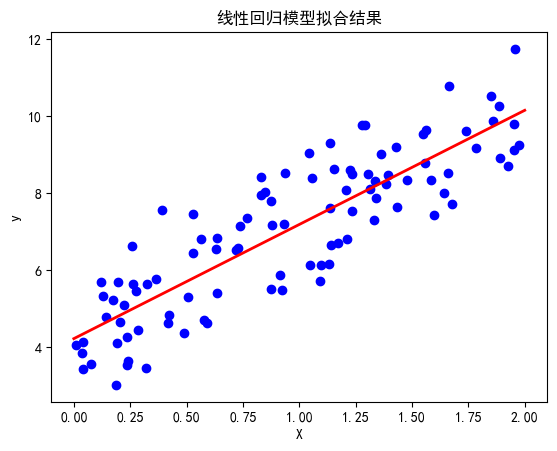
在这个demo中:
- 蓝色的点代表生成的模拟小球。
- 红色的线表示线性回归模型的拟合结果。
模型的线性方程为 $ y = 2.97X + 4.22 $。这里,2.97是斜率,4.22是截距。这个方程告诉我们,X和Y之间存在正相关关系,每增加一个单位的X,Y平均增加2.97个单位。
这个demo展示了如何用Python和scikit-learn库快速构建和可视化一个简单的线性回归模型。你可以在PyCharm或其他Python环境中运行这段代码,更好地理解和实践线性回归。
希望这个解释能帮助你更好地理解线性回归模型!如果你有任何问题,或者想要更深入地了解,随时问我哦!😊🎈