k-means聚类算法&k-means++聚类算法
聚类(Clustering) 是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。也就是说,聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
聚类算法的一般过程
- **数据准备:**包括特征标准化和降维;
- **特征选择:**从最初的特征中选择最有效的特征,并将其存储于向量中;
- **特征提取:**通过对所选择的特征进行转换形成新的突出特征;
- **聚类(或分组):**首先选择合适特征类型的某种距离函数(或构造新的距离函数)进行接近程度的度量,而后执行聚类或分组;
- **聚类结果评估:**是指对聚类结果进行评估,评估主要有3种:外部有效性评估、内部有效性评估和相关性测试评估。

二、Kmeans算法
2.1原理
Kmeans 算法是一种常用的聚类算法,它是基于划分方法聚类的。它的原理是将数据划分为k个簇,每个簇由距离中心最近的数据点组成,基于计算样本与中心点的距离归纳各簇类下的所属样本,迭代实现样本与其归属的簇类中心的距离为最小的目标。
简单来说,Kmeans 算法就是通过不断地调整簇的中心点,并将数据点指派到距离它最近的中心点所在的簇,来逐步将数据划分成若干个簇。
常见目标函数:

2.2算法步骤

算法执行步骤如下:
- 选取K个点做为初始聚集的簇心(也可选择非样本点);
- 分别计算每个样本点到 K个簇核心的距离(这里的距离一般取欧氏距离或余弦距离),找到离该点最近的簇核心,将它归属到对应的簇;
- 所有点都归属到簇之后, M个点就分为了 K个簇。之后重新计算每个簇的重心(平均距离中心),将其定为新的“簇核心”;
- 反复迭代 2 - 3 步骤,直到达到某个中止条件。
【注意】常用的中止条件有迭代次数、最小平方误差MSE、簇中心点变化率
2.3k值确定
Kmeans划分k个簇,不同k值的情况对最终结果的影响至关重要,不同的k值会带来不同的结果,如下图所示:
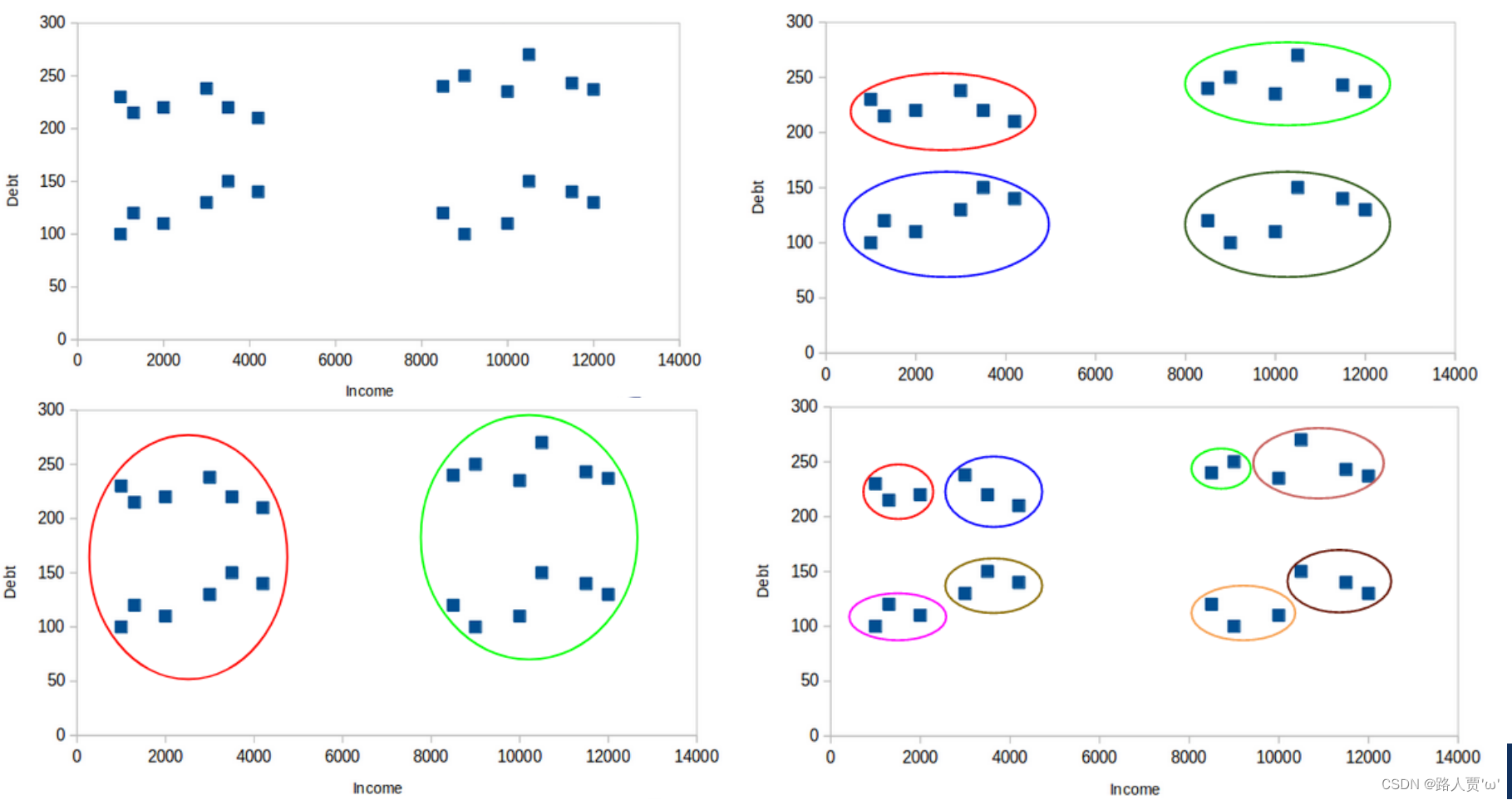
一般情况下,我们确定k值常用两种方法:先验法、手肘法
2.3.1先验法
先验法比较简单,就是凭借着业务知识确定k的取值。比如对于iris花数据集,我们大概知道有三种类别,可以按照k=3做聚类验证。从下图可看出,对比聚类预测与实际的iris种类是比较一致的。
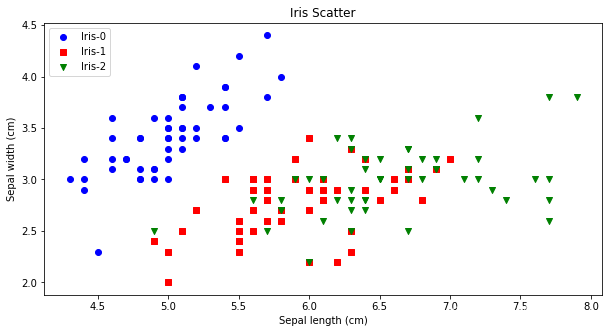
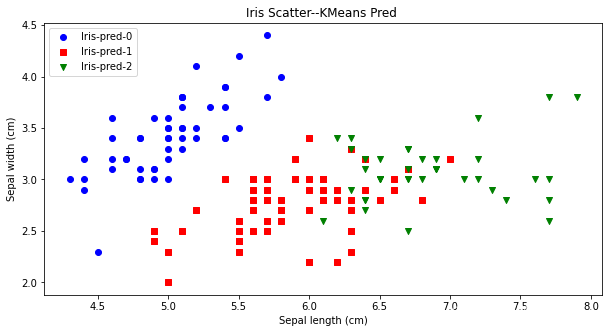
2.3.2手肘法
可以知道k值越大,划分的簇群越多,对应的各个点到簇中心的距离的平方的和(类内距离,WSS)越低,我们通过确定WSS随着K的增加而减少的曲线拐点,作为K的取值。
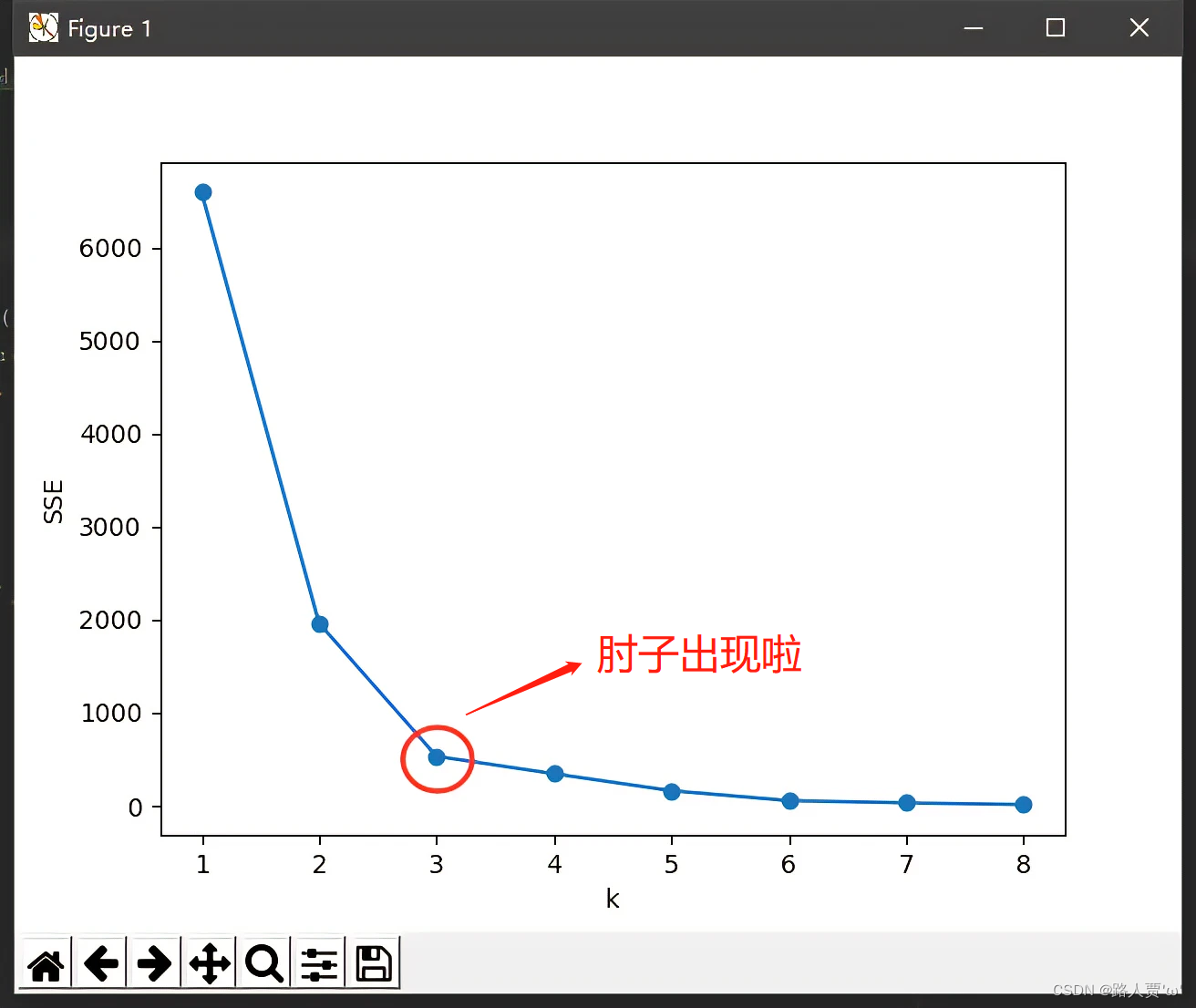
2.4代码实现
Kmeans具体代码如下:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def assignment(df, center, colmap):
# 计算所有样本分别对K个类别中心点的距离
for i in center.keys():
df["distance_from_{}".format(i)] = np.sqrt((df["x"] - center[i][0]) ** 2 + (df["y"] - center[i][1]) ** 2)
distance_from_centroid_id = ['distance_from_{}'.format(i) for i in center.keys()]
df["closest"] = df.loc[:, distance_from_centroid_id].idxmin(axis=1) # "closest"列表示每个样本点离哪个类别的中心点距离最近
print(df["closest"])
df["closest"] = df["closest"].map(lambda x: int(x.lstrip('distance_from_')))
df["color"] = df['closest'].map(lambda x: colmap[x])
return df
def update(df, centroids):
# 更新K个类别的中心点
for i in centroids.keys():
# 每个类别的中心点为 属于该类别的点的x、y坐标的平均值
centroids[i][0] = np.mean(df[df['closest'] == i]['x'])
centroids[i][1] = np.mean(df[df['closest'] == i]['y'])
return centroids
def main():
df = pd.DataFrame({
'x': [12, 20, 28, 18, 10, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 64, 69, 72, 23],
'y': [39, 36, 30, 52, 54, 20, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 19, 7, 24, 77]
})
k = 3
# 一开始随机指定 K个类的中心点
center = {
i: [np.random.randint(0, 80), np.random.randint(0, 80)]
for i in range(k)
}
colmap = {0: "r", 1: "g", 2: "b"}
df = assignment(df, center, colmap)
for i in range(10): # 迭代10次
closest_center = df['closest'].copy(deep=True)
center = update(df, center) # 更新K个类的中心点
df = assignment(df, center, colmap) # 类别中心点更新后,重新计算所有样本点到K个类别中心点的距离
if closest_center.equals(df['closest']): # 若各个样本点对应的聚类类别不再变化,则结束聚类
break
plt.scatter(df['x'], df['y'], color=df['color'], alpha=0.5, edgecolor='b')
for j in center.keys():
plt.scatter(*center[j], color=colmap[j], linewidths=6)
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()
if __name__ == '__main__':
main()
实现效果:
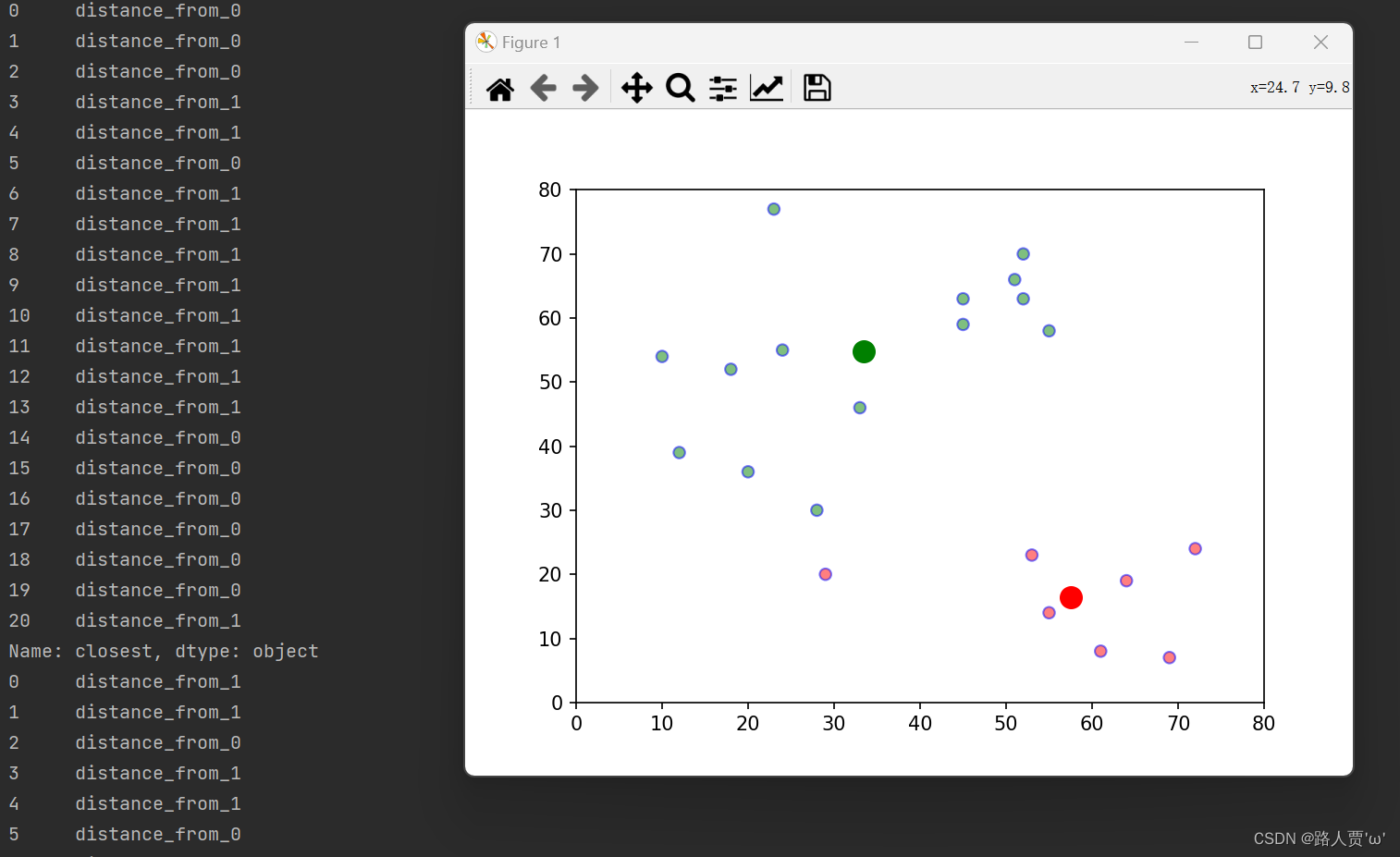
2.5优缺点
*优点:*
- 理解容易,聚类效果不错
- 处理大数据集的时候,该算法可以保证较好的伸缩性和高效率
- 当簇近似高斯分布的时候,效果非常不错
*缺点:*
- K值是用户给定的,在进行数据处理前,K值是未知的,给定合适的 k 值,需要先验知识,凭空估计很困难,或者可能导致效果很差
- 对初始簇中心点是敏感的
- 不适合发现非凸形状的簇或者大小差别较大的簇
- 特殊值(离群值或称为异常值)对模型的影响比较大
三、Kmeans++算法
3.1原理
原始Kmeans算法最开始随机选取数据集中k个点作为聚类中心,k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心。如果仅仅是完全随机的选择,有可能导致算法收敛很慢。**Kmeans++算法主要对对K-Means初始值选取的方法的优化。**也就是说,Kmeans++算法与Kmeans算法最本质的区别是在k个聚类中心的初始化过程。
3.2算法步骤
其实通过上面的介绍,我们知道了 Kmeans++算法和Kmeans算法就是选择一开始的k个聚类中心点的方法有差别而已。其初始点的选择过程如下:
- 从数据点中随机选择一个中心。
- 对于每个数据点x,计算D(x),即x与已经选择的最接近中心之间的距离。
- 使用加权概率分布随机选择一个新的数据点作为新的中心,其中选择点 x 的概率与D(x)^2成正比。
- 重复步骤2和3,直到选择了K个中心。
其余训练过程与KMeans一致。
3.3代码实现
Kmeans++具体代码如下:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
def select_center(first_center, df, k, colmap):
center = {}
center[0] = first_center
for i in range(1, k):
df = assignment(df, center, colmap)
sum_closest_d = df.loc[:, 'cd'].sum() # cd = 最近中心点的距离。把所有样本点对应最近中心点的距离都加在一起
df["p"] = df.loc[:, 'cd'] / sum_closest_d
sum_p = df["p"].cumsum()
# 下面是轮盘法取新的聚类中心点
next_center = random.random()
for index, j in enumerate(sum_p):
if j > next_center:
break
center[i] = list(df.iloc[index].values)[0:2]
return center
def assignment(df, center, colmap):
# 计算所有样本分别对K个类别中心点的距离
for i in center.keys():
df["distance_from_{}".format(i)] = np.sqrt((df["x"] - center[i][0]) ** 2 + (df["y"] - center[i][1]) ** 2)
distance_from_centroid_id = ['distance_from_{}'.format(i) for i in center.keys()]
df["closest"] = df.loc[:, distance_from_centroid_id].idxmin(axis=1) # "closest"列表示每个样本点离哪个类别的中心点距离最近
df["cd"] = df.loc[:, distance_from_centroid_id].min(axis=1)
df["closest"] = df["closest"].map(lambda x: int(x.lstrip('distance_from_')))
df["color"] = df['closest'].map(lambda x: colmap[x])
return df
def update(df, centroids):
# 更新K个类别的中心点
for i in centroids.keys():
# 每个类别的中心点为 属于该类别的点的x、y坐标的平均值
centroids[i][0] = np.mean(df[df['closest'] == i]['x'])
centroids[i][1] = np.mean(df[df['closest'] == i]['y'])
return centroids
def main():
df = pd.DataFrame({
'x': [12, 20, 28, 18, 10, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 64, 69, 72, 23],
'y': [39, 36, 30, 52, 54, 20, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 19, 7, 24, 77]
})
k = 3
colomap = {0: "r", 1: "g", 2: "b"}
first_center_index = random.randint(0, len(df) - 1)
first_center = [df['x'][first_center_index], df['y'][first_center_index]]
center = select_center(first_center, df, k, colomap)
df = assignment(df, center, colomap)
for i in range(10): # 迭代10次
closest_center = df['closest'].copy(deep=True)
center = update(df, center) # 更新K个类的中心点
df = assignment(df, center, colomap) # 类别中心点更新后,重新计算所有样本点到K个类别中心点的距离
if closest_center.equals(df['closest']): # 若各个样本点对应的聚类类别不再变化,则结束聚类
break
plt.scatter(df['x'], df['y'], color=df['color'], alpha=0.5, edgecolor='b')
for j in center.keys():
plt.scatter(*center[j], color=colomap[j], linewidths=6)
plt.xlim(0, 80)
plt.ylim(0, 80)
plt.show()
if __name__ == '__main__':
main()
实现效果:
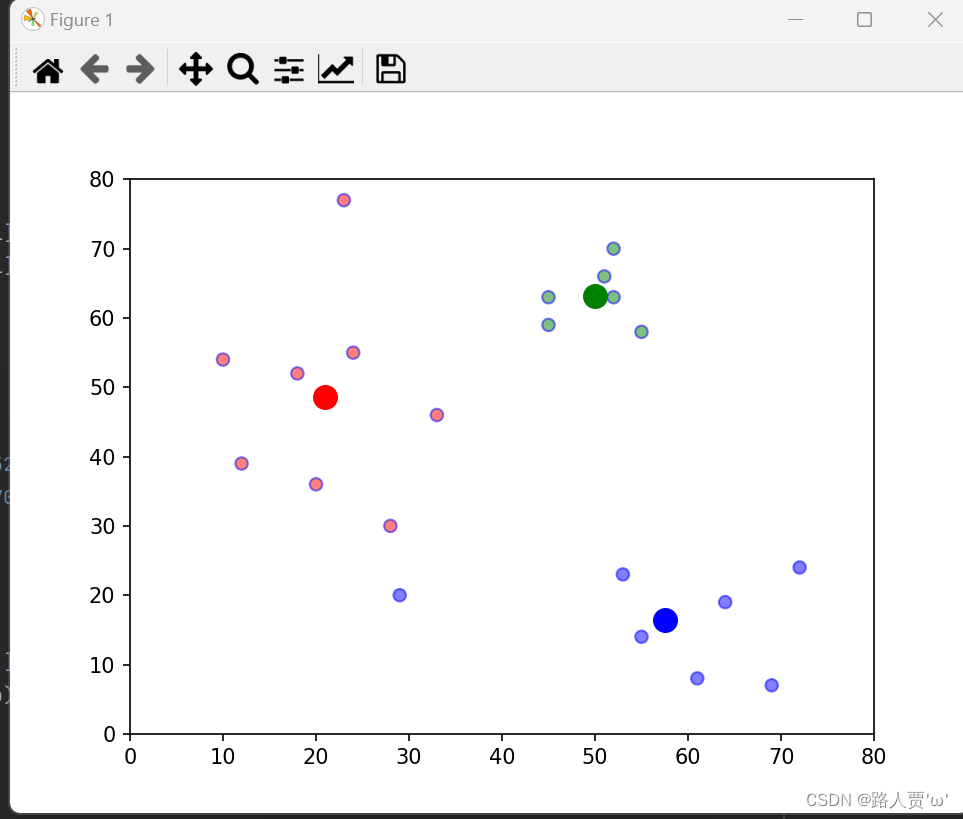
3.4优缺点
*优点:*
- 避免了Kmeans随机选取k个聚类中心导致可能聚类中心选择的不好,最终对结果会产生很大的影响的问题
- 在目标检测应用中,Kmeans++通过改变初始聚类中心的生成方式,增大初始锚框之间差距,使锚框更适应整体据分布,得到了匹配度更好的多尺度锚框,进而提升了模型的检测性能。
*缺点:*
- 由于聚类中心点选择过程中的内在有序性,在扩展方面存在着性能方面的问题(第k个聚类中心点的选择依赖前k-1个聚类中心点的值)。
附录
k-means++代码:http://rosettacode.org/wiki/K-means%2B%2B_clustering
参考文章:聚类算法:Kmeans和Kmeans++算法精讲-阿里云开发者社区 (aliyun.com)
*缺点:**
- 由于聚类中心点选择过程中的内在有序性,在扩展方面存在着性能方面的问题(第k个聚类中心点的选择依赖前k-1个聚类中心点的值)。
附录
k-means++代码:http://rosettacode.org/wiki/K-means%2B%2B_clustering
参考文章:聚类算法:Kmeans和Kmeans++算法精讲-阿里云开发者社区 (aliyun.com)