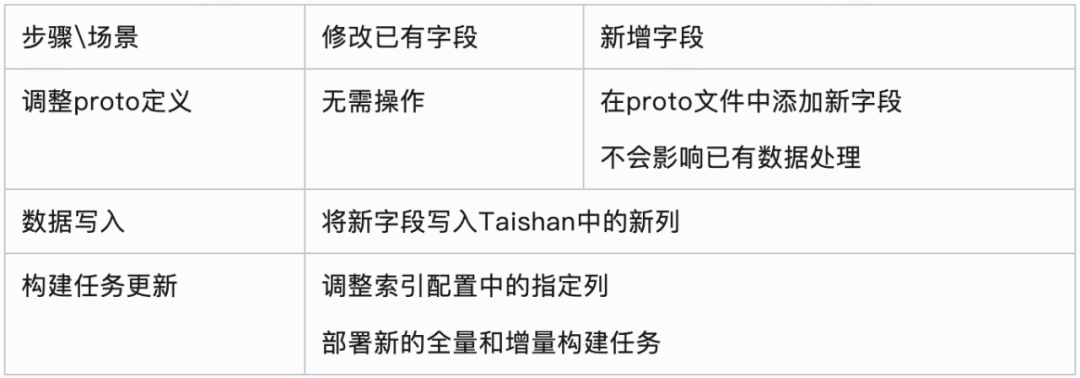
优质博文:IT-BLOG-CN
一、题目
给定三个字符串s1、s2、s3,请你帮忙验证s3是否是由s1 和s2交错 组成的。
两个字符串s和t交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空
子字符串:
s = s1 + s2 + ... + sn
t = t1 + t2 + ... + tm
|n - m| <= 1
交错 是s1 + t1 + s2 + t2 + s3 + t3 + ... 或者t1 + s1 + t2 + s2 + t3 + s3 + ...
注意:a + b意味着字符串a和b连接。
示例 1:

输入:s1 = "aabcc",s2 = "dbbca",s3 = "aadbbcbcac"
输出:true
示例 2:
输入:s1 = "aabcc",s2 = "dbbca",s3 = "aadbbbaccc"
输出:false
示例 3:
输入:s1 = "",s2 = "",s3 = ""
输出:true
提示:
0 <=s1.length, s2.length <= 100
0 <= s3.length <= 200
s1、s2、和s3都由小写英文字母组成
二、代码
方法一:动态规划
记 ∣s1∣=n,∣s2∣=m
思路与算法
双指针法错在哪里? 也许有同学看到这道题目的第一反应是使用双指针法解决这个问题,指针p1一开始指向s1的头部,指针p2一开始指向s2的头部,指针p3指向s3的头部,每次观察p1和p2指向的元素哪一个和p3指向的元素相等,相等则匹配并后移指针。样例就是一个很好的反例,用这种方法判断s1=aabcc,s2=dbbca,s3=aadbbcbcac时,得到的结果是False,实际应该是True。
解决这个问题的正确方法是动态规划。 首先如果∣s1 ∣+∣s2∣=∣s3∣,那s3必然不可能由s1和s2交错组成。在∣s1∣+∣s2∣=∣s3∣时,我们可以用动态规划来求解。我们定义f(i,j)表示s1的前i个元素和s2的前j个元素是否能交错组成s3的前i+j个元素。如果s1的第i个元素和s3的第i+j个元素相等,那么s1的前i个元素和s2的前j个元素是否能交错组成s3的前i+j个元素取决于s1的前i−1个元素和s2的前j个元素是否能交错组成s3的前i+j−1个元素,即此时f(i,j)取决于f(i−1,j),在此情况下如果f(i−1,j)为真,则f(i,j)也为真。同样的,如果s2的第j个元素和s3的第i+j个元素相等并且f(i,j−1)为真,则f(i,j)也为真。于是我们可以推导出这样的动态规划转移方程:
f(i,j)=[f(i−1,j)ands1 (i−1)=s3(p)]or[f(i,j−1)ands2 (j−1)=s3(p)]
其中p=i+j−1。边界条件为f(0,0)=True。至此,我们很容易可以给出这样一个实现:
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
int n = s1.length(), m = s2.length(), t = s3.length();
if (n + m != t) {
return false;
}
boolean[][] f = new boolean[n + 1][m + 1];
f[0][0] = true;
for (int i = 0; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
int p = i + j - 1;
if (i > 0) {
f[i][j] = f[i][j] || (f[i - 1][j] && s1.charAt(i - 1) == s3.charAt(p));
}
if (j > 0) {
f[i][j] = f[i][j] || (f[i][j - 1] && s2.charAt(j - 1) == s3.charAt(p));
}
}
}
return f[n][m];
}
}
不难看出这个实现的时间复杂度和空间复杂度都是O(nm)。
使用滚动数组优化空间复杂度。 因为这里数组f的第i行只和第i−1行相关,所以我们可以用滚动数组优化这个动态规划,这样空间复杂度可以变成O(m)。敲黑板:我们又遇到「滚动数组」优化啦!不会的同学一定要学习哟。
下面给出滚动数组优化的代码。
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
int n = s1.length(), m = s2.length(), t = s3.length();
if (n + m != t) {
return false;
}
boolean[] f = new boolean[m + 1];
f[0] = true;
for (int i = 0; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
int p = i + j - 1;
if (i > 0) {
f[j] = f[j] && s1.charAt(i - 1) == s3.charAt(p);
}
if (j > 0) {
f[j] = f[j] || (f[j - 1] && s2.charAt(j - 1) == s3.charAt(p));
}
}
}
return f[m];
}
}
时间复杂度: O(nm),两重循环的时间代价为O(nm)。
空间复杂度: O(m),即s2的长度。