原文链接： https://tecdat.cn/?p=37338

原文出处：拓端数据部落公众号

分析师：Jixin Zhong 

 本文将通过视频讲解，展示如何用滚动回归预测，并结合一个R语言多元时间序列滚动预测：ARIMA、回归、ARIMAX模型分析实例的代码数据，为读者提供一套完整的实践数据分析流程。

滚动回归估计是于一个大规模样本范畴内，以滚动的形式接连选取一系列的小规模样本，并运用与大规模样本相同的方式对小规模样本的参数予以估计。

样本固定的长度被称为“window”，每次递增的步长则被称作“step”。从普通最小二乘法（OLS）模型的结果中获取的“coef”值能够用于查看系数，进而构建方程。

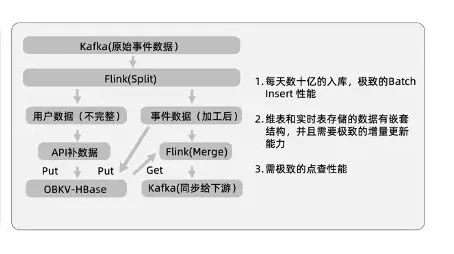
 滚动窗口回归在预测GDP中的应用

 

2021 年的预测方程如下：

 

其中，为 2020 年 GDP，为 2020 年失业率，为 2020 年贷款利率，为 2020 年存款利率，为 2020 年货币供应量，为 2021 年的预测 GDP。所得到的预测值为 1113629.18253568。

优点

滚动回归可用于剖析变量之间的因果关系以及动态演变过程。通过系数能够阐释被解释变量对于解释变量变化的敏感性，从而进一步明晰每个解释变量对通胀的影响脉络。

缺点

Python 不像 R 语言，在进行滚动回归操作时，没有现成可用的函数来处理。倘若使用传统的“for 循环”来进行回归，当样本数量在 1 万以上时，运算速度会非常缓慢。

R语言多元时间序列滚动预测：ARIMA、回归、ARIMAX模型分析 

 

当需要为数据选择最合适的预测模型或方法时，预测者通常将可用的样本分成两部分：内样本（又称 "训练集"）和保留样本（或外样本，或 "测试集"）。然后，在样本中估计模型，并使用一些误差指标来评估其预测性能。

如果这样的程序只做一次，那么这被称为 "固定原点 "评估。然而，时间序列可能包含离群值，一个差的模型可能比更合适的模型表现得更好。为了加强对模型的评估，我们使用了一种叫做 "滚动原点 "的方法。

滚动原点是一种预测方法，根据这种方法，预测原点被连续更新，预测是由每个原点产生的（Tashman 2000）。这种方法允许获得几个时间序列的预测误差，从而更好地了解模型的表现。

如何实现呢？

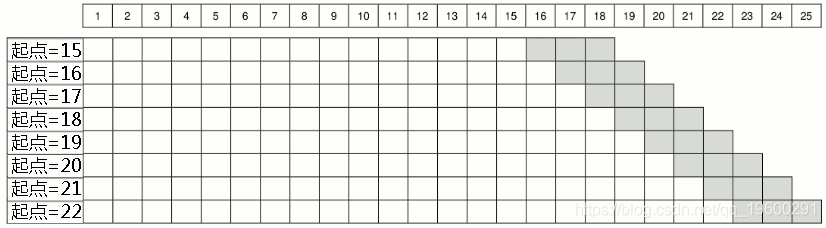
下图描述了滚动原点的基本思想。白色单元格对应的是样本内数据，而浅灰色单元格对应的是前三步的预测。该图中时间序列有25个观测值，预测从8个原点开始产生，从原点15开始。模型在每次迭代中都被重新估计，并产生预测结果。之后，在系列的末尾增加一个新的观测值，这个过程继续进行。当没有更多的数据需要添加时，这个过程就会停止。这可以被认为是一个滚动的原点，有一个固定的保留样本量。这个程序的结果是产生了8个一到三步的预测。在此基础上，我们可以计算出误差测量方法，并选择表现最好的模型。

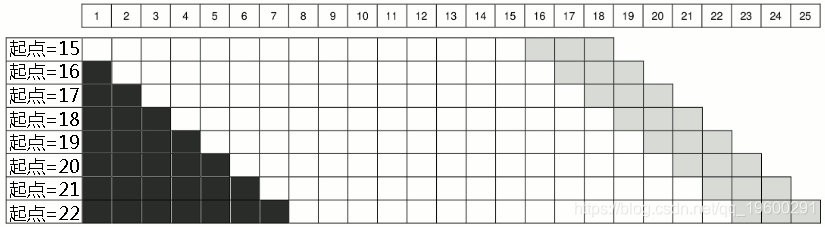
从8个原点产生预测的另一个选择是，从原点17而不是15开始（见下图）。在这种情况下，程序一直持续到原点22，即产生最后一个三步超前预测的时候，然后继续以递减的预测范围进行。因此，两步预测从原点23产生，只有一步预测从原点24产生。因此，我们得到8个一步预测，7个两步预测和6个三步预测。这可以被认为是一个滚动的原点，有一个非固定的保留样本量。可用于在小样本的情况下，当我们没有多余的观测值的时候。

最后，在上述两种情况下，我们的样本量都在增加。然而对于某些研究目的，我们可能需要一个恒定的内样本。下图展示了这样一种情况。在这种情况下，在每次迭代中，我们在系列的末尾增加一个观察值，并从系列的开始删除一个观察值（深灰色单元）。

R实现：一元时间序列ARIMA案例

R实现了对任何函数的滚动原点估计，有一个预定义的调用，并返回预期的值。

我们从一个简单的例子开始，从正态分布生成序列。

x <- rnorm(100,100,10)

我们在这个例子中使用ARIMA(0,1,1)。

predict(arima(x=data,order=c(0,1,1)),n.ahead=h

调用包括两个重要元素：data和h。data指定了样本内值在我们要使用的函数中的位置。h将告诉我们的函数，在选定的函数中指定了预测的范围。在这个例子中，我们使用arima(x=data,order=c(0,1,1))，产生了一个想要的ARIMA(0,1,1)模型，然后我们使用predict(...,n. ahead=h)，从该模型产生一个预测。

还需要指定函数应该返回什么。可以是条件平均数（点预测），预测区间，模型的参数。然而，根据你使用的函数返回的内容，滚动预测返回的内容有一些不同。如果它是一个矢量，那么滚动预测将产生一个矩阵（列中有每个原点的值）。如果它是一个矩阵，那么就会返回一个数组。最后，如果它是一个列表，那么将返回一个列表的列表。

我们先从predict()函数中收集条件平均值。

我们可以使用滚动原点从模型中产生预测结果。比方说，我们想要三步预测和8个原点，所有其他参数的默认值。

predro(x, h , orig )

该函数返回一个列表，其中包含我们要求的所有数值，再加上保留样本的实际数值。我们可以根据这些值计算一些基本的误差指标，例如，按比例的平均绝对误差。

apply(abs(holdo - pred),1,mean) / mean(actual)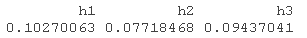

在这个例子中，我们使用apply()函数，区分不同的预测期，并了解模型在每个预测期的表现。以类似的方式，我们可以评估其他一些模型的性能，并与第一个模型产生的误差进行比较。这些数字本身并不能说明什么，但如果我们把这个模型的表现与另一个模型进行比较，那么我们就可以推断出一个模型是否比另一个模型更适合数据。

我们还可以绘制来自滚动原点的预测结果。

plot(Values1)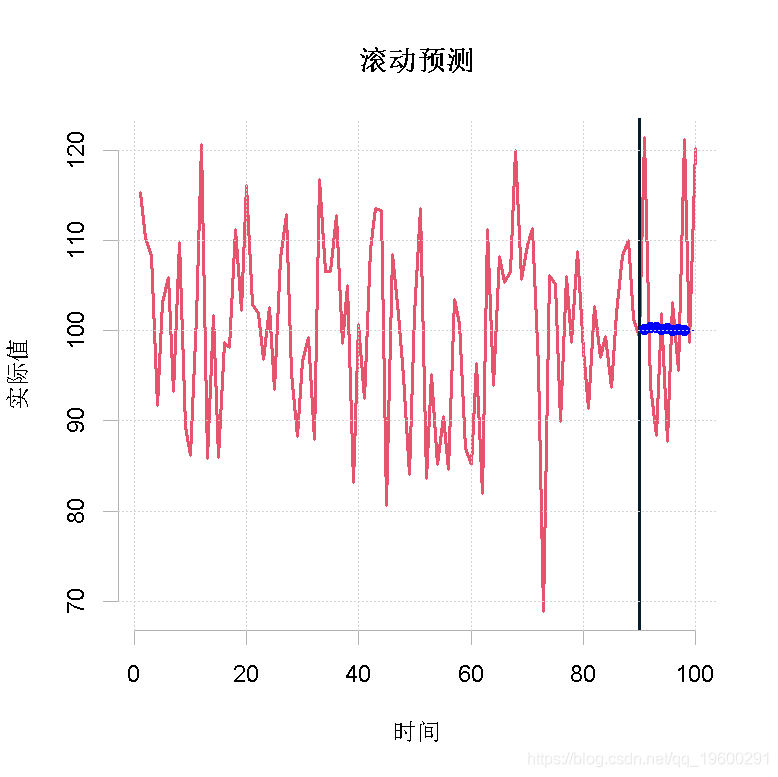

在这个例子中，来自不同来源的预测结果是相互接近的。这是因为数据是平稳的，模型是相当稳定的。

如果我们看一下返回的矩阵，我们会注意到它们包含缺失值。

这是因为在默认情况下，保留样本被设置为非常数。内样本也被设置为非常数，这就是为什么模型在每次迭代时都会对增加的样本进行重新估计。我们可用修改这一点。

predro(x, h , ori )

请注意，return2的值与return1的值不能直接比较，因为它们是由不同的起点生成的。这一点在我们绘图时可以看出来。

plot(returned2)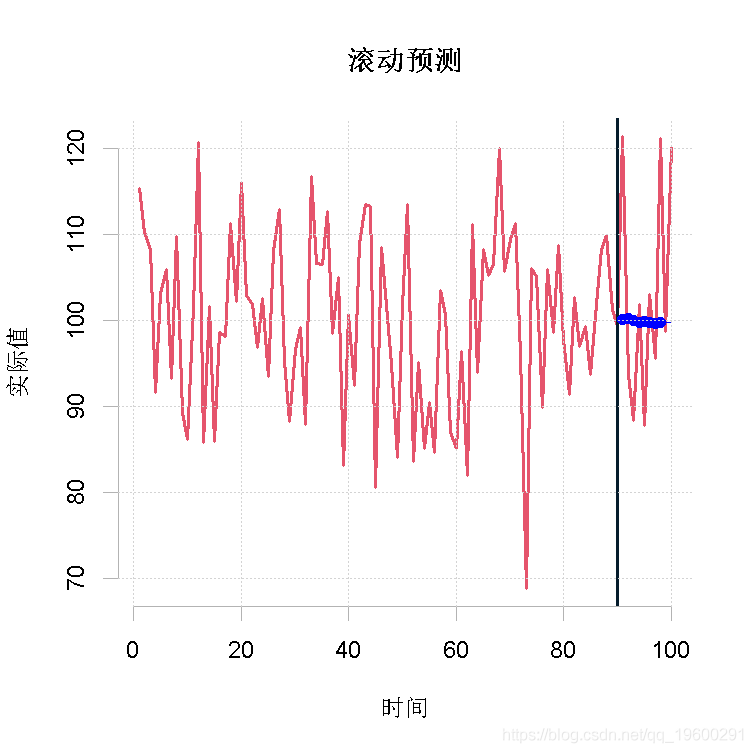

如果你使用预测包中的函数，可以用以下方式修改调用和返回值。

 "forecast(ets(data) ,level=95"
 c("mean","lower","upper")

多元时间序列ARIMA案例

当你有一个模型和一个时间序列时,滚动预测的是一个方便的方法。但是如果你需要将不同的模型应用于不同的时间序列呢？我们会需要一个循环。在这种情况下，有一个简单的方法来使用滚动预测。现在引入几个时间序列。

对于这个例子，我们需要一个返回值的数组。

array(NA,c(3,2,3,8))

在这里，我们将有3个时间序列，2个模型和来自8个来源的3步超前预测。我们的模型将被保存在一个单独的列表中。在这个例子中，我们将有ARIMA（0,1,1）和ARIMA（1,1,0）。

 list(c(0,1,1), c(1,1,0))

我们从函数中返回相同的预测值，但我们需要改变调用方式，因为现在我们必须将这两种不同的模型考虑在内。

"predict(arima(data,Models\[\[i\]\])ahead=h)"

我们没有直接指定模型，而是使用列表中的第i个元素。

我们还想从保留样本中保存实际值，以便能够计算误差。

这个数组有3个时间序列和来自8个原点的3步超前预测的维度。

最后，我们可以写一个循环并产生预测结果。

for(j in 1:3)  for(i in 1:2)predro(data, h , or=8)

比较两者在不同时间序列上的表现。

exp(mean(log(apply(Holdout - Fore  / apply(abs(Holdout - Fore ))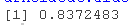

因此，根据这些结果，可以得出结论，在我们的三个时间序列上，ARIMA（0,1,1）平均来说比ARIMA（1,1,0）更准确。

线性回归和ARIMAX案例

我们的最后一个例子，我们创建数据框并拟合线性回归。

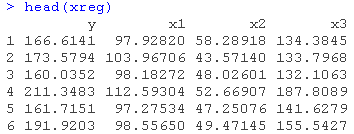
请注意，在这个例子中，lm()函数中实现的回归依赖于数据框架，不使用预测范围。

predict(lm(y~x1+x2+x3,xre),newdat

此外，函数predict.lm()返回的是一个带有数值的矩阵，而不是一个列表。 最后调用滚动预测。

pred(y, h , ori  )

在这种情况下, 我们需要在调用的数据参数中提供因变量, 因为该函数需要提取holdout的值.

predict(lm( xreg ,new =xreg "
predro( $y, h , or  )
plot( Return)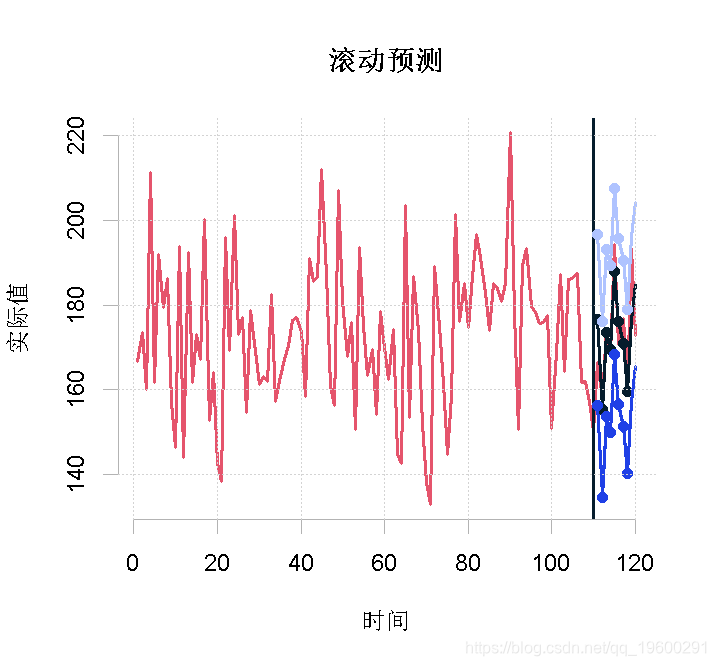

作为最后一个例子，我们考虑以下数据的ARIMAX模型。

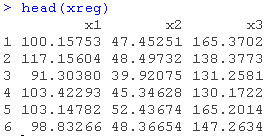
并相应地修改调用。

ourCall <- "predict(arima(x=data, order=c(0,1,1), xreg=xreg\[counti,\]), n.ahead=h, newxreg=xreg\[counto,\])"

考虑到现在我们处理的是ARIMA，我们需要同时指定数据和h。此外，xreg与之前的例子不同，因为它现在不应该包含因变量。

如果你使用ETSX模型，调用可以简化为：

 "es(x=dat, xreg, h=h"

最后，上面提到的所有例子都可以并行完成，特别是当数据非常多且样本量很大时。

参考文献

Davydenko, Andrey, and Robert Fildes. 2013. “Measuring Forecasting Accuracy: The Case of Judgmental Adjustments to Sku-Level Demand Forecasts.” _International Journal of Forecasting_ 29 (3). Elsevier B.V.: 510–22. Redirecting.

Petropoulos, Fotios, and Nikolaos Kourentzes. 2015. “Forecast combinations for intermittent demand.” _Journal of the Operational Research Society_ 66 (6). Nature Publishing Group: 914–24. https://doi.org/10.1057/jors.2014.62.

---

关于分析师

 

在此对 Jixin Zhong 对本文所作的贡献表示诚挚感谢，她在中南财经政法大学完成了信息管理与信息系统的学位，专注信息领域。擅长 Python 、深度学习、数据采集 。