【C++】多源BFS问题和拓扑排序

多源BFS介绍

单源BFS和多源BFS的区别

SO如何解决多源BFS问题

多源之核心

矩阵

算法思路

代码实现

飞地的数量

算法思路

代码实现

地图中的最高点

算法思路

代码实现

地图分析

算法思路

代码实现

拓扑排序介绍

有向无环图

编辑

如何解决这类问题

课程表

算法思路

代码实现

课程表2

算法思路

代码实现

火星词典

代码实现

多源BFS介绍

单源BFS和多源BFS的区别

顾名思义，单源BFS是只有一个起点，博客CSDN中已经阐述过，如有不明白者，可前去一探究竟，而多源BFS是有多个起点，然后同时出发，到达终点；

SO如何解决多源BFS问题

多源的BFS，本质上与单源的BFS并无太大差别，我们只需要把多个起点等效成一个起点即可，这样就转化为了单源的问题了。

多源之核心

将所有的起点都加入队列---->扩散----->终点。与单源之秘法极其类似，方能解之。

矩阵

例题地址. - 力扣（LeetCode）

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

算法思路

对于求的最终结果，我们有两种⽅式：

• 第⼀种⽅式：从每⼀个 1 开始，然后通过层序遍历找到离它最近的 0 。

这⼀种⽅式，我们会以所有的 1 起点，来⼀次层序遍历，势必会遍历到很多重复的点。并且如果

矩阵中只有⼀个 0 的话，每⼀次层序遍历都要遍历很多层，时间复杂度较⾼。

• 换⼀种⽅式：从 0 开始层序遍历，并且记录遍历的层数。当第⼀次碰到 1 的时候，当前的层数

就是这个 1 离 0 的最短距离。

这⼀种⽅式，我们在遍历的时候标记⼀下处理过的 1 ，能够做到只⽤遍历整个矩阵⼀次，就能得

到最终结果。

但是，这⾥有⼀个问题， 0 是有很多个的，我们怎么才能保证遇到的 1 距离这⼀个 0 是最近呢？

其实很简单，我们可以先把所有的 0 都放在队列中，把它们当成⼀个整体，每次把当前队列⾥⾯的所有元素向外扩展⼀次。

代码实现

class Solution {
public:
    int m,n;
    int dx[4]={1,-1,0,0};
    int dy[4]={0,0,1,-1};
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        m=mat.size();n=mat[0].size();
        vector<vector<int>>ans(m,vector<int>(n,-1));
        queue<pair<int,int>>q;
        //储存所有的原点
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(mat[i][j]==0)
                {
                    q.push({i,j});
                    ans[i][j]=0;
                }
            }
        }
        int ret=0;
        while(q.size())
        {
            ret++;
            int sz=q.size();
            while(sz--)
            {
                auto [a,b]=q.front();
                q.pop();
                for(int i=0;i<4;i++)
                {
                    int x=a+dx[i];int y=b+dy[i];
                    if(x>=0&&x<m&&y>=0&&y<n&&ans[x][y]==-1)
                    {
                        ans[x][y]=ret;
                        q.push({x,y});
                    }
                }
            }
        }
        return ans;
    }
};

飞地的数量

例题地址：. - 力扣（LeetCode）

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次移动是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

算法思路

正难则反：

从边上的 1 开始搜索，把与边上 1 相连的联通区域全部标记⼀下；

然后再遍历⼀遍矩阵，看看哪些位置的 1 没有被标记即可

标记的时候，可以⽤「多源 bfs 」。

代码实现

class Solution {
public:
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    int numEnclaves(vector<vector<int>>& grid) {
        int m=grid.size();int n=grid[0].size();
        bool vis[m][n];
        memset(vis,0,sizeof vis);
        queue<pair<int,int>>q;
        //储存原点
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if((i==0||i==m-1||j==0||j==n-1))
                {
                    if(grid[i][j]==1)
                    {
                    q.push({i,j});
                    vis[i][j]=true;
                    }
                }
            }
        }
        while(q.size())
        {
                auto [a,b]=q.front();
                q.pop();
                for(int i=0;i<4;i++)
                {
                    int x=a+dx[i];int y=b+dy[i];
                    if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&!vis[x][y])
                    {
                        q.push({x,y});
                        vis[x][y]=true;
                    }                        
                }
        }
        int ret=0;
        for(int i=0;i<m;i++)
        for(int j=0;j<n;j++)
        if(grid[i][j]==1&&!vis[i][j])
        ret++;
        return ret;
    }
};

地图中的最高点

地址：. - 力扣（LeetCode）

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由陆地和水域单元格组成的地图。

如果 isWater[i][j] == 0 ，格子 (i, j) 是一个陆地格子。
如果 isWater[i][j] == 1 ，格子 (i, j) 是一个水域格子。

你需要按照如下规则给每个单元格安排高度：

每个格子的高度都必须是非负的。
如果一个格子是水域，那么它的高度必须为 0 。
任意相邻的格子高度差至多为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值最大。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：

输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。

示例 2：

输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案

算法思路

代码实现

class Solution {
public:
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    int numEnclaves(vector<vector<int>>& grid) {
        int m=grid.size();int n=grid[0].size();
        bool vis[m][n];
        memset(vis,0,sizeof vis);
        queue<pair<int,int>>q;
        //储存原点
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if((i==0||i==m-1||j==0||j==n-1))
                {
                    if(grid[i][j]==1)
                    {
                    q.push({i,j});
                    vis[i][j]=true;
                    }
                }
            }
        }
        while(q.size())
        {
                auto [a,b]=q.front();
                q.pop();
                for(int i=0;i<4;i++)
                {
                    int x=a+dx[i];int y=b+dy[i];
                    if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&!vis[x][y])
                    {
                        q.push({x,y});
                        vis[x][y]=true;
                    }                        
                }
        }
        int ret=0;
        for(int i=0;i<m;i++)
        for(int j=0;j<n;j++)
        if(grid[i][j]==1&&!vis[i][j])
        ret++;
        return ret;
    }
};

地图分析

地址：. - 力扣（LeetCode）

你现在手里有一份大小为 n x n 的网格 grid，上面的每个单元格都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

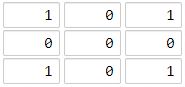
输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

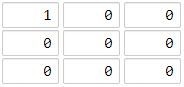
输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

算法思路

代码实现

class Solution {
public:
    int dx[4]={1,-1,0,0};
    int dy[4]={0,0,1,-1};
    int maxDistance(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        vector<vector<bool>>vis(m,vector<bool>(n));//标记数组
        //将所有的1作为起点
        queue<pair<int,int>>q;
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(grid[i][j]==1)
                {
                    q.push({i,j});
                }
            }
        }
        int ret=0;
        if(q.size()==n*n||q.size()==0)retur n -1;
        while(q.size())
        {
            ret++;
            int sz=q.size();
            while(sz--)
            {
                auto [a,b]=q.front();
                q.pop();
                for(int i=0;i<4;i++)
                {
                    int x=a+dx[i];int y=b+dy[i];
                    if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==0&&!vis[x][y])
                    {
                        q.push({x,y});
                        vis[x][y]=true;
                    }
                }
            }
        }
        return ret-1;
    }
};

拓扑排序介绍

有向无环图

入度：指向活动节点的箭头个数；
出度：从活动节点出去指向别的节点的箭头个数。

通过入度和出入我们可以判断活动的进行顺序，活动度数为0的活动先进行没进行完后，将该活动的出度清空，下一个入度为0的节点就是该节点之后要进行的活动，以此类推，直到最后没有活动节点，如果只存在有一个入度的节点(成环)。

如何解决这类问题

1.首先建图，也就是邻接矩阵，可以使用哈希表处理。
2.统计所有活动节点的出度和入度。
3.如果入度是0就把活动节点加入到队列中。
4.BFS每走一步就把该节点的出度清空，将下一个入度为0的节点加入队列中。
5.判断是否有环：遍历度数表，如果还存在度数不为0的活动节点，那么说明还有活动成环了；

课程表

地址：. - 力扣（LeetCode）

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

算法思路

a. 将所有⼊度为 0 的点加⼊到队列中；

b. 当队列不空的时候，⼀直循环：

i. 取出队头元素；

ii. 将于队头元素相连的顶点的⼊度 - 1；

iii. 然后判断是否减成 0,。如果减成 0，就加⼊到队列中。

代码实现

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        //首先构造邻接矩阵,也就是边
        int n=numCourses;
        unordered_map<int,vector<int>>edge;
        //储存每一个节点的入度
        //先把所有的节点放在了数组中
        vector<int>in(n);//后面要统计所有课程的度数是否为零
        //储存所有的边
        for(auto &x:prerequisites)
        {
            int a=x[0];//最红的课程(终点)
            int b=x[1];//先学的课程(起点)
            //存进数组中
            edge[b].push_back(a);
            in[a]++;//对应节点的入度增加
        }
        //开始使用队列来处理无度数的节点
        queue<int>q;
        for(int i=0;i<n;i++)
        if(in[i]==0)
        q.push(i);//如果入度为零，就加入到队列
        while(q.size())
        {
            //取出无度数的节点
            auto tmp=q.front();
            q.pop();
            //然后取消所有与他有关的边
            for(auto& x: edge[tmp])
            {
                in[x]--;
                //是否要加入后面的课程
                if(in[x]==0)//如果没有度数了
                {
                    q.push(x);
                }
            }

        }
        //判断是否有环
        for(auto i:in)
        {
            if(i)//如果存在度数不为0的节点
            return false;
        }
        return true;
    }
};

课程表2

地址：. - 力扣（LeetCode）

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前必须先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2：

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3]

示例 3：

输入：numCourses = 1, prerequisites = []
输出：[0]

算法思路

与上一道题一样。

代码实现

class Solution {
public:
    vector<int> findOrder(int n, vector<vector<int>>& p) {
            unordered_map<int,vector<int>>edge;
            //储存所有的节点
            vector<int>in(n);//统计所有节点的度数

            //建图
            for(auto &e:p)
            {
                int a=e[0];//终点
                int b=e[1];//起点
                edge[b].push_back(a);
                in[a]++;//终点的入度数增加
            }

            //DFS
            queue<int>q;
            for(int i=0;i<n;i++)
            if(in[i]==0)
            q.push(i);//储存所有的入度为零的节点.
            //储存结果的数组
            vector<int>ret;
            while(q.size())
            {
                auto t=q.front();
                q.pop();
                ret.push_back(t);
                for(auto x:edge[t])//遍历节点后的链接的节点
                {
                    in[x]--;
                    if(in[x]==0)
                    {
                        q.push(x);
                    }
                }
            }
            //判断是否有环
            for(auto x:in)
            if(x)return {};
            return ret;
    }
};

火星词典

地址：. - 力扣（LeetCode）

现有一种使用英语字母的外星文语言，这门语言的字母顺序与英语顺序不同。

给定一个字符串列表 words ，作为这门语言的词典，words 中的字符串已经 按这门新语言的字母顺序进行了排序 。

请你根据该词典还原出此语言中已知的字母顺序，并 按字母递增顺序 排列。若不存在合法字母顺序，返回 "" 。若存在多种可能的合法字母顺序，返回其中 任意一种 顺序即可。

字符串 s 字典顺序小于 字符串 t 有两种情况：

在第一个不同字母处，如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前，那么 s 的字典顺序小于 t 。
如果前面 min(s.length, t.length) 字母都相同，那么 s.length < t.length 时，s 的字典顺序也小于 t 。

示例 1：

输入：words = ["wrt","wrf","er","ett","rftt"]
输出："wertf"

示例 2：

输入：words = ["z","x"]
输出："zx"

示例 3：

输入：words = ["z","x","z"]
输出：""
解释：不存在合法字母顺序，因此返回 "" 。

代码实现

class Solution {
public:
    unordered_map<char,unordered_set<char>>edge;
    unordered_map<char,int>in;
    string alienOrder(vector<string>& words) {
        for(auto &str:words)
        {
            for(auto x:str)
            {
                in[x]=0;
            }
        }
        int n=words.size();
        for(int i=0;i<n;i++)
        for(int j=i+1;j<n;j++)
        {
            bool tmp=add(words[i],words[j]);
            if(tmp==true)return "";
        }

        queue<char>q;
        for(auto [a,b]:in)
        {
            if(b==0)q.push(a);
        }
        string ret;
        while(q.size())
        {
            auto t=q.front();
            q.pop();
            ret+=t;
            for(auto x:edge[t])
            {
                if(--in[x]==0)q.push(x);
            }
        }

        for(auto [a,b]:in)
        if(b)return "";
        return ret;
    }


    bool add(string & s1,string&s2)
    {
        int n=min(s1.size(),s2.size());
        int i=0;
        for(;i<n;i++)
        {
            if(s1[i]!=s2[i])
            {
                char a=s1[i];
                char b=s2[i];
                if(!edge.count(a)||!edge[a].count(b))
                {
                    edge[a].insert(b);
                    in[b]++;
                }
                break;
            }
        }
        if(i==s2.size()&&i<s1.size())return true; 
        return false;
    }
};