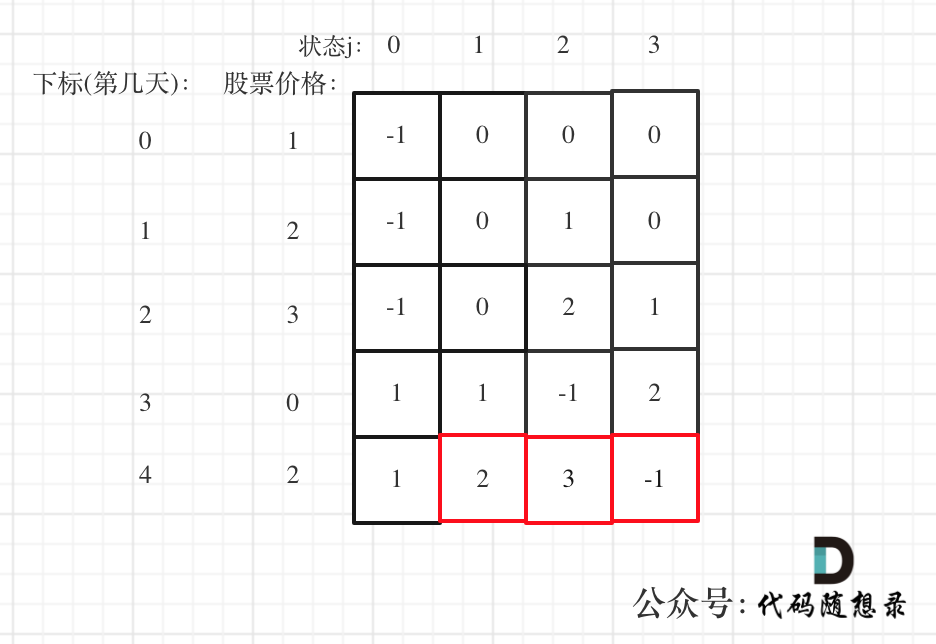
为了搞清楚快速排序的效率，我们先从分区开始。分解来看，你会发现它包含两种步骤。

❏ 比较：每个值都要与轴做比较。

❏ 交换：在适当时候将左右指针所指的两个值交换位置。

一次分区至少有N次比较，即数组的每个值都要与轴做比较。因为每次分区时，左右指针都会从两端开始靠近，直到相遇。

交换的次数则取决于数据的排列情况。一次分区里，交换最少会有1次，最多会有N / 2次，因为即使所有元素都需要交换，我们也只是将左半部分与右半部分进行交换，如下图所示。

对于随机排列的数据，粗略来算就是N / 2的一半，即N / 4次交换。于是，N次比较加上N / 4次交换，共1.25N步。最后根据大O记法的规则，忽略常数项，得出分区操作的时间为O(N)。

这就是一次分区的效率。但完整的快速排序需要对多个数组以及不同大小的子数组分区，想知道整个过程所花的时间，还要再进一步分析才行。

为了更形象地描述，我们将一个含有8个元素的数组的快速排序过程画了出来。它旁边有每一次分区所作用的元素个数。由于元素值并不重要，因此就不显示了。注意，作用范围就是那些白色的格子。

这里有8次分区，但每次作用的范围大小不一。因为只含1个元素的子数组就是基准情形，无须任何交换和比较，所以只有元素量大于或等于2的子数组才要算分区。

由于此例属于平均情况的一种，因此我们假设每次分区大约要花1.25N步，得出：

如果再对不同大小的数组做统计，你会发现N个元素，就要N×log N步。想体会什么是N×log N的话，可参考下表。

在上面一个数组含8个元素的例子中，快速排序花了大约21步，也很接近8×log8（等于24）​。这种时间复杂度的算法我们还是第一次遇到，用大O记法来表达的话，它是O(N log N)算法。

快速排序的步数接近N×log N绝非偶然。如果我们以更平均的情况来考察快速排序，就能看出原因了。

快速排序开始时会对整个数组进行分区。假设此次分区会将轴最终安放到数组中央——这也是平均情况——然后我们就要对由此切开的两半进行分区。巧合的是，它们的轴也最终落在各自的中央，分出4个大小为原数组四分之一的子数组。并且，接下来所有分区都出现了这种轴在中央的情况。

这样一来，我们基本上就是在不断地对半切分子数组，直至产生出的子数组长度为1。那么，一个数组要经历多少次分区才能切到这么小呢？如果数组元素有N个，那就是log N次。假设元素有8个，那就要对半切3次，才能分出只有1个元素的子数组。这个原理你应该在二分查找那节学过了。对两个新的子数组所执行的分区操作，需要处理的数据量还是相当于对原数组所做的分区。如下图所示。

因为等分发生了log N次，而每次都要对总共N个元素做分区，所以总步数为N×log N。

之前我们看到的很多算法，最佳情况都发生在元素有序的时候。但在快速排序里，最佳情况应该是每次分区后轴都刚好落在子数组的中间。

最坏情况

快速排序最坏的情况就是每次分区都使轴落在数组的开头或结尾。导致这种情况的原因有好几种，包括数组已升序排列，或已降序排列。下面我们把这种情况用图来说明一下。

虽然在此情况下，每次分区都只有一次交换，但比较的次数却变得很多。在轴总落在中央的例子里，每次分区都能划分出比原数组小得多的子数组（过程中产生的最大的子数组长度为4）​，使各部分都能很快地到达基准情形。然而如果轴落在其中一端，前5次分区就需要处理长度大于4的数组。而且这5次分区里，每次所需的比较次数还是和子数组的元素量一样多。

于是在最坏情况下，对8 + 7 + 6 + 5 + 4 + 3 + 2个元素进行分区，一共35次比较。

写成公式的话，就是N个元素，需要N + (N -1) + (N -2) + (N -3) + … + 2步，即/ 2步，如下图所示。

又因为大O忽略常数，所以最终我们会说，快速排序最坏情况下的效率为O()。既然把快速排序分析完了，我们将它与插入排序比较一下。

虽然快速排序在最好情况和最坏情况都没能超越插入排序，但在最常遇见的平均情况，前者的O(Nlog N)比后者的O()好得多，所以总体来说，快速排序优于插入排序。

以下是各种时间复杂度的对比。

由于快速排序在平均情况下表现优异，于是很多编程语言自带的排序函数都采用它来实现。因此一般你不需要自己写快速排序。但你可能需要学会写快速选择——它是一种类似快速排序的实用算法。