深度学习——神经网络(neural network)详解(一). 带手算步骤,步骤清晰0基础可看
我将以最简单,基础的形式说明神经网络的训练过程。
搭配以下文章进行学习:
深度学习——卷积神经网络(convolutional neural network)CNN详解(一)——概述. 步骤清晰0基础可看
深度学习——卷积神经网络(convolutional neural network)CNN详解(二)——前向传播与反向传播过程(特征提取+预测+反向传播更新参数). 步骤清晰0基础可看
深度学习——神经网络(neural network)详解(一). 带手算步骤,步骤清晰0基础可看
深度学习——神经网络(neural network)详解(二). 带手算步骤,步骤清晰0基础可看
机器学习/深度学习——梯度下降法(Gradient descent)详解. 步骤清晰 0基础可看
一、训练神经网络概述
训练神经网络是利用大量已知数据(训练数据)来调整网络参数(权重和偏置),使网络能够学习输入数据到输出数据的映射关系的过程。
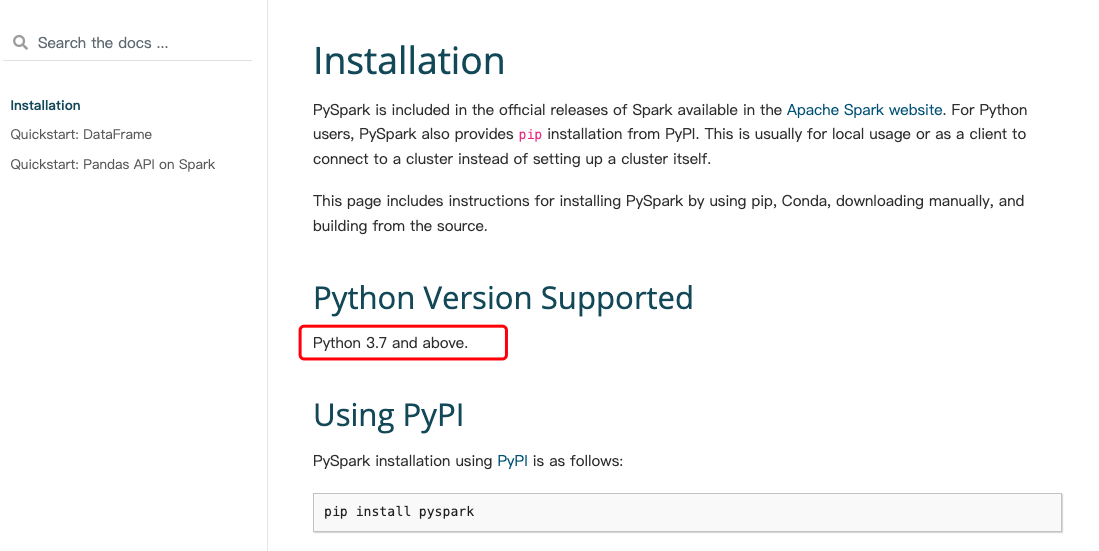
基础的神经网络可以分为,输入层(Input Layer),隐藏层 (Hidden Layers),输出层(Output Layer),如下图所示。
在这之前,我们先来了解几个概念。
1.输入层 (Input Layer): 输入层是神经网络的第一层,负责接收网络的输入数据。每个神经元对应一个输入特征。
2.输出层 (Output Layer): 输出层是神经网络的最后一层,负责产生最终的预测结果。在分类问题中,输出层的神经元数量通常等于类别数。
3.隐藏层 (Hidden Layers): 隐藏层位于输入层和输出层之间,可以有多个。隐藏层的目的是提取输入数据的特征并进行组合,以便于网络学习复杂的模式。
4.神经元 (Neurons): 神经元是网络的基本单元,每个神经元接收来自前一层神经元的输出,对它们进行加权求和,然后可能通过一个激活函数来生成自己的输出。
5.权重 (Weights): 权重是神经元之间连接的强度,它们决定了信号在网络中的传递程度。权重是网络在训练过程中学习得到的参数。
6.偏置 (Biases): 偏置是加在神经元输入上的一个常数项,它为模型提供了平移的自由度,使得模型可以更好地拟合数据。
7.激活函数 (Activation Function): 激活函数是一个数学函数,用于在神经元的输出上引入非线性。这使得神经网络能够学习和模拟复杂的函数映射。常见的激活函数包括Sigmoid、Tanh、ReLU等。
激活函数其实就是把上一层的输出转变到你想要的范围内,是一个映射函数,方便进行下一层的操作。比如归一化就是一个映射操作。
8.损失函数 (Loss Function):损失函数用于衡量模型的预测输出与实际标签之间的差异。它是评估模型性能的指标,常见的损失函数包括均方误差、交叉熵损失等。

神经网络图示详解
1. 输入层
输入层有两个神经元,分别表示输入特征,
x
1
x_{1}
x1 ,
x
2
x_{2}
x2。
x
=
[
x
1
x
2
]
x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}
x=[x1x2]
2. 隐藏层
隐藏层有三个神经元,分别表示 h 1 h_{1} h1 , h 2 h_{2} h2 , h 3 h_{3} h3 。输入层和隐藏层之间的连接具有权重 w 1 w_{1} w1 到 w 6 w_{6} w6,并且每个隐藏层神经元都有一个偏置 b b b。这就是网络的参数,我们需要更新的就是权重 w w w和偏置 b b b这些网络参数,使这个神经网络能够越来越适应我们的任务,最后能够对新输入做出较为准确的预测判断。
对于隐藏层的每个神经元,计算如下:
-
对于第一个隐藏层神经元 h 1 h_{1} h1:
h 1 = σ ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) h_1 = \sigma(w_{1}x_1 + b_1+ w_{4}x_2 + b_4) h1=σ(w1x1+b1+w4x2+b4) -
对于第二个隐藏层神经元 h 2 h_{2} h2:
h 2 = σ ( w 2 x 1 + b 2 + w 5 x 2 + b 5 ) h_2 = \sigma(w_{2}x_1 + b_2+ w_{5}x_2 + b_5) h2=σ(w2x1+b2+w5x2+b5) -
对于第三个隐藏层神经元 h 3 h_{3} h3:
h 3 = σ ( w 3 x 1 + b 3 + w 6 x 2 + b 6 ) h_3 = \sigma(w_{3}x_1 + b_3+ w_{6}x_2 + b_6) h3=σ(w3x1+b3+w6x2+b6)
这里, σ \sigma σ表示激活函数,如ReLU或Sigmoid。
3. 输出层
输出层有一个神经元 y ^ \hat{y} y^,表示最终的输出。隐藏层和输出层之间的连接具有权重 w 7 w_{7} w7 到 w 9 w_{9} w9。
输出层神经元的计算
输出神经元
y
^
\hat{y}
y^ 的计算如下,
σ
\sigma
σ表示激活函数:
y
^
=
σ
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
\hat{y} = \sigma(w_7 h_1 + w_8 h_2 + w_9 h_3)
y^=σ(w7h1+w8h2+w9h3)
到此为止,输入 x 1 x_{1} x1 , x 2 x_{2} x2经过这个神经网络特征呗提取到了,因为我们利用这个神经网络获取到了 x 1 x_{1} x1 , x 2 x_{2} x2的具体输出。
接下来我们以房价预测为例来说明神经网络参数的更新过程,也就是神经网络的训练过程。
损失函数
L = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 L = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y}_i)^2 L=n1i=1∑n(yi−y^i)2
二、房价预测情景
何为训练神经网络? 假设我们要预测明年的房价,可以将神经网络视为一个预测函数 f(x),其中 x 代表影响房价的各种因素:
- 房屋面积(平方米)
- 房屋位置(市中心或郊区)
- 房屋年龄(年)
- 周边设施(学校、医院、交通等)
- 市场趋势和经济指标(GDP增长率、通货膨胀率等)
我们的目标是使用神经网络学习这些因素与房价之间的关系,并预测未来的房价。
三、运算过程概述
1. 数据收集
收集历史房价数据及相关影响因素。
2. 数据预处理
对数据进行归一化处理,使输入特征 x 在相同尺度上,预处理的操作有很多种,在实际模型训练的过程中我们需要用到较为复杂的预处理过程。
3. 构建神经网络
设计一个神经网络结构,例如包含输入层、隐藏层和输出层的简单网络。
4. 初始化参数
随机初始化网络中的权重和偏置。
5. 前向传播
使用训练数据集,计算每个输入 x 通过神经网络的预测输出 ŷ = f(x)。
6. 计算损失
使用均方误差(MSE)作为损失函数,计算预测值与实际房价之间的差异:
L
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
L = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y}_i)^2
L=n1i=1∑n(yi−y^i)2
在这个公式中:
- L L L 表示损失函数的输出,即所有样本损失的均值。
- n n n 是训练集中的样本数量。
- y i y_{i} yi是第 i i i 个样本的实际值。
- y ^ i \hat{y}_{i} y^i 是第 i i i个样本的预测值。
**样本:**样本指的是一组包含房屋特征和对应房价的数据点。每个样本都代表了市场上的一个具体的房产实例,它通常包含多个特征以及该房产的销售价格。即一个样本代表一个数据对,包含实际的输入 x x x和对应的输出 y y y。输出 y y y即为真实值,Ground Truth。我们的目标是通过调整模型的参数来最小化损失函数 L L L,从而提高预测的准确性。
例如,在房价预测模型中,如果我们使用两个特征:房屋面积 x 1 x_{1} x1和房屋位置 x 2 x_{2} x2,则模型的预测输出可以表示为 y ^ \hat{y} y^,而实际的房价为 y y y。
7. 反向传播
计算损失函数关于每个参数的梯度,使用链式法则反向传播。
(1)链式法则的基本原理:
设有一个由多个函数复合而成的复合函数 ( F = f(g(x)) ),链式法则允许我们通过计算以下形式来求得 ( F ) 的导数:
d F d x = d f d g ⋅ d g d x \frac{dF}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx} dxdF=dgdf⋅dxdg
这里:
-
d
f
d
g
\frac{df}{dg}
dgdf是外函数
f
f
f对中间变量
g
g
g 的导数。
-
d
g
d
x
\frac{dg}{dx}
dxdg 是内函数
g
g
g对原始变量
x
x
x 的导数。
(2)链式法则在神经网络中的应用:
在神经网络中,前向传播可以看作是多个层级和激活函数的复合。损失函数 L L L 是关于输出 y ^ \hat{y} y^的函数,而输出 y ^ \hat{y} y^本身是关于网络参数(如权重 w w w 和偏置 b b b的复合函数。
反向传播中的链式法则:
-
从输出层开始:计算损失函数 L L L对输出 y ^ \hat{y} y^的梯度,这通常很简单,因为大多数损失函数(如均方误差)对输出的导数有明确的解析解。
-
逐层反向传播:从输出层开始,逆向通过网络的每一层,使用链式法则计算损失函数对每一层参数的梯度。对于每一层:
∂ L ∂ a \frac{\partial L}{\partial a} ∂a∂L是当前层的激活函数 a a a的导数(即激活函数的导数)。 -
参数更新:使用计算得到的梯度和选择的优化算法(如梯度下降)更新网络的参数。
具体到这个例子,梯度具体计算过程如下:
L
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
L = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y}_i)^2
L=n1∑i=1n(yi−y^i)2
y
^
=
σ
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
\hat{y} = \sigma(w_7 h_1 + w_8 h_2 + w_9 h_3)
y^=σ(w7h1+w8h2+w9h3)
h
1
=
σ
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
h_1 = \sigma(w_{1}x_1 + b_1+ w_{4}x_2 + b_4)
h1=σ(w1x1+b1+w4x2+b4)
h
2
=
σ
(
w
2
x
1
+
b
2
+
w
5
x
2
+
b
5
)
h_2 = \sigma(w_{2}x_1 + b_2+ w_{5}x_2 + b_5)
h2=σ(w2x1+b2+w5x2+b5)
h
3
=
σ
(
w
3
x
1
+
b
3
+
w
6
x
2
+
b
6
)
h_3 = \sigma(w_{3}x_1 + b_3+ w_{6}x_2 + b_6)
h3=σ(w3x1+b3+w6x2+b6)
由损失函数求
w
w
w和
b
b
b两个参数的梯度的公式如下。当然,
w
1
w_{1}
w1到
w
9
w_{9}
w9对应不同的公式。
d
L
d
w
=
d
L
d
y
^
⋅
d
y
^
d
w
+
d
L
d
y
^
⋅
d
y
^
d
h
⋅
d
h
d
w
\frac{dL}{dw} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dw} +\frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh} \cdot \frac{dh}{dw}
dwdL=dy^dL⋅dwdy^+dy^dL⋅dhdy^⋅dwdh
d L d b = d L d y ^ ⋅ d y ^ d w + d L d y ^ ⋅ d y ^ d h ⋅ d h d w \frac{dL}{db} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dw} +\frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh} \cdot \frac{dh}{dw} dbdL=dy^dL⋅dwdy^+dy^dL⋅dhdy^⋅dwdh
比如对于
w
1
w_{1}
w1,其求导公式为:
d
L
d
w
1
=
d
L
d
y
^
⋅
d
y
^
d
h
1
⋅
d
h
1
d
w
1
\frac{dL}{dw_{1}} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh_{1}} \cdot \frac{dh_{1}}{dw_{1}}
dw1dL=dy^dL⋅dh1dy^⋅dw1dh1
8. 参数更新,即更新权重和偏置
(1)梯度下降法
使用梯度下降法(Gradient descent)更新网络参数:
梯度下降法是一种优化方法,用于最小化一个函数,通常在机器学习和人工智能中用于最小化损失函数,从而找到模型参数的最佳值。具体的思想可以自己去查资料了解,这里只需要知道相关参数是怎么进行更新的就行了。这里的
α
\alpha
α叫做学习率,控制着梯度下降的大小。
w n e w = α ⋅ ∂ L ∂ w o l d w ^{new}= \alpha \cdot \frac{\partial L}{\partial w^{old}} wnew=α⋅∂wold∂L
让我们来分析一下这个公式,减号代表着在每次迭代中,参数按照损失函数梯度的相反方向更新,因为向梯度的相反方向移动可以减少损失函数的值。
梯度(Gradient):梯度是一个向量,指向损失函数增长最快的方向。数学上,梯度是损失函数对每个参数偏导数的集合。
损失函数减少:在优化问题中,我们的目标是最小化损失函数。损失函数衡量了模型预测值与实际值之间的差异。
参数更新:在梯度下降法中,我们通过调整模型的参数来减少损失函数的值。
相反方向:梯度指向损失增加的方向,因此,为了减少损失,我们需要向梯度的相反方向更新参数。
举个例子,如果损失函数是一个山谷地形,那么梯度就是指向山谷坡度最陡峭的方向。梯度下降法就像是沿着最陡的下坡路往下走,直到找到山谷的最低点,这个最低点就是损失函数的最小值。
9. 迭代优化
重复步骤5到8,直到满足停止条件。
在梯度下降法中,停止条件用于确定何时停止迭代过程。以下是一些常用的停止条件:
最大迭代次数:设置一个最大迭代次数,例如1000次迭代。这是一个简单的停止条件,可以防止无限循环。
损失函数的阈值:如果损失函数的值低于某个预设的阈值(例如0.001),则认为模型已经足够好,可以停止迭代。
10. 模型评估
使用验证集或测试集评估模型的预测性能。
有多种评估方式来对机器学习/深度学习模型进行评估,在这个房价预测的背景下,我们可以采取如下指标:
均方误差和均方根误差
准确性是衡量模型预测结果与实际值接近程度的指标。在房价预测中,通常使用均方误差(Mean Squared Error, MSE)或者均方根误差(Root Mean Squared Error, RMSE)来衡量误差的大小。MSE和RMSE越小,表示模型的预测结果与实际值越接近。
-
均方误差 (MSE):
M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 {MSE} = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y}_i)^2 MSE=n1i=1∑n(yi−y^i)2 -
均方根误差 (RMSE):
R M S E = M S E {RMSE} = \sqrt{MSE} RMSE=MSE