二、存储结构
文章目录
- 二、存储结构
- ❗1.邻接矩阵
- 1.1无向图
- ❗邻接矩阵-无向图代码-C
- 1.2有向图
- ❗邻接矩阵-有向图代码-C
- 1.3带权图
- 1.4性能分析
- 1.5相乘
- ❗2.邻接表
- 2.1无向图
- 2.2有向图
- ❗邻接表-C
- 邻接矩阵VS邻接表
- 邻接矩阵
- 邻接表
❗1.邻接矩阵
图的邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
用1表示有边,0表示没有边。

结点数为n的图G,邻接矩阵A是一个n*n的方阵,将G顶点编号为
v
1
,
v
2
,
.
.
.
,
v
n
v_1,v_2,...,v_n
v1,v2,...,vn:
A
[
i
]
[
j
]
=
{
1
,
若边集
E
(
G
)
中有
(
v
i
,
v
j
)
o
r
<
v
i
,
v
j
>
0
,
若边集
E
(
G
)
中没有
(
v
i
,
v
j
)
o
r
<
v
i
,
v
j
>
A[i][j] = \begin{cases} 1, & 若边集E(G)中有(v_i,v_j)or<v_i,v_j> \\[2ex] 0, & 若边集E(G)中没有(v_i,v_j)or<v_i,v_j> \end{cases}
A[i][j]=⎩
⎨
⎧1,0,若边集E(G)中有(vi,vj)or<vi,vj>若边集E(G)中没有(vi,vj)or<vi,vj>
存储结构定义:
#define MaxVertexNum 100 //顶点数目的最大值
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
typedef struct{
VertexType Vex[MaxVertexNum] ; //顶点表:存放结构or信息
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, edgenum; //图的当前顶点数和边数/弧数
}MGraph;
1.1无向图
-
无向图的邻接矩阵一定是一个对称矩阵(即从矩阵的左上角到右下角的主对角线为轴,右上角的元与左下角相对应的元全都是相等的)。
因此,在存储邻接矩阵时只需存储上(或下)三角矩阵的元素。
-
对于无向图,第i个结点的度 = 邻接矩阵的**第i行(或第i列)**非零元素(或非∞元素)的个数。
顶点A的度就是0+1+1+1+0+0=3。
❗邻接矩阵-无向图代码-C
/* 图
邻接矩阵(Adjacency Matrix)
存储方式是用两个数组来表示图。
一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
无向图
C实现
*/
#include <stdio.h>
#include <string.h>
#define MaxVertexNum 100 //顶点数目最大值
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
#define numVertexes 6 // 顶点个数,用于visited数组
#define numEdges 7 // 边个数
typedef struct
{
VertexType Vex[MaxVertexNum]; //顶点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, edgenum; //图的顶点数和弧数
}MGraph;
void create_Graph(MGraph *G);
void create_Graph_ByArray(MGraph *G, int edges[][3]);
void print_Matrix(MGraph G);
void DFS(MGraph G,int v);
void DFSTraverse(MGraph G);
void BFS(MGraph G, int v);
void BFSTraverse(MGraph G);
int main()
{
MGraph G;
// 创建无向图方法1
//create_Graph(&G);
// 创建无向图方法2
//这里可以使用int,因为edge的EdgeType是int
int edges[numEdges][3] = { // 边的起点序号,终点序号,权值
{1,2,5},
{1,3,1},
{1,4,6},
{2,5,3},
{2,6,4},
{3,5,3},
{4,6,2}
};
create_Graph_ByArray(&G,edges);
print_Matrix(G);
printf("\nDFS:");
DFS(G,0);
printf("\nBFS:");
BFS(G,0);
printf("\nBFS直接遍历(非连通图):");
BFSTraverse(G);
return 0;
}
// 创建无向图
void create_Graph(MGraph *G){
int i, j;
int start, end; //边的起点序号、终点序号
int w; //边上的权值
// 所创建无向图的顶点数和边数(用空格隔开)。这里也可以输入
G->vexnum = numVertexes;
G->edgenum = numEdges;
printf("\n");
//图的初始化init
for (i=0; i<G->vexnum; i++){
for (j=0; j<G->vexnum; j++){
if (i == j)
G->Edge[i][j] = 0; //结点自身
else
G->Edge[i][j] = 32767; //初始都为表示∞
}
}
//顶点信息存入顶点表
for (i=0; i<G->vexnum; i++){
// printf("请输入第%d个顶点的信息(int):",i+1);
// scanf("%d", &G->Vex[i]);
//这里不输入了,暂时默认0开始
G->Vex[i] = i+1;
}
printf("\n");
//输入无向图边的信息
for (i=0; i<G->edgenum; i++){
printf("请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):");
scanf("%d%d%d", &start, &end, &w);
G->Edge[start-1][end-1] = w;
G->Edge[end-1][start-1] = w; //无向图具有对称性
}
}
// 创建无向图
void create_Graph_ByArray(MGraph *G, int edges[][3]){
int i, j;
int start, end; //边的起点序号、终点序号
int w; //边上的权值
// 所创建无向图的顶点数和边数(用空格隔开)。这里也可以输入
G->vexnum = numVertexes;
G->edgenum = numEdges;
printf("\n");
//图的初始化init
for (i=0; i<G->vexnum; i++){
for (j=0; j<G->vexnum; j++){
if (i == j)
G->Edge[i][j] = 0; //结点自身
else
G->Edge[i][j] = 32767; //初始都为表示∞
}
}
//顶点信息存入顶点表
for (i=0; i<G->vexnum; i++){
// printf("请输入第%d个顶点的信息(int):",i+1);
// scanf("%d", &G->Vex[i]);
//这里不输入了,暂时默认0开始
G->Vex[i] = i+1;
}
printf("\n");
// 输入无向图边的信息
for (i=0; i<G->edgenum; i++){
start = edges[i][0];
end = edges[i][1];
w = edges[i][2];
G->Edge[start-1][end-1] = w;
G->Edge[end-1][start-1] = w; //无向图具有对称性
}
}
// 输出图
void print_Matrix(MGraph G){
int i, j;
printf("\n图的顶点为:");
for (i=0; i<G.vexnum; i++)
printf("%d ", G.Vex[i]);
printf("\n输出邻接矩阵:\n");
// 横坐标
printf(" "); //表示行坐标,前面空格留给纵坐标
for (i=0; i<G.vexnum; i++)
printf("%5d", G.Vex[i]);
printf("\n");
for (i=0; i<G.vexnum; i++){
// 纵坐标
printf("\n%d", G.Vex[i]);
// 输出邻接矩阵
for (j=0; j<G.vexnum; j++){
if (G.Edge[i][j] == 32767)
printf("%7s", "∞");
else
printf("%5d", G.Edge[i][j]);
}
printf("\n");
}
}
// ------------------------- DFS 深度优先遍历------------------------
int visited[numVertexes]={0};
// 注意:是从0下标开始
void DFS(MGraph G, int x){
// 访问顶点x
printf("%d",G.Vex[x]);
visited[x]=1; //设已访问标记
// 遍历x的邻接顶点
for(int v=0; v<G.vexnum; v++){
//i为x的尚未访问的邻接顶点
if(!visited[v] && G.Edge[x][v] != 32767){
DFS(G, v);
}
}
}
//对非连通图进行深度优先遍历
void DFSTraverse(MGraph G){
//把所有结点全部标记为false,表示没有访问过
for(int v=0; v<G.vexnum; v++){
visited[v] = 0;
}
for(int v=0; v<G.vexnum; v++){ //从v=0开始遍历
if(!visited[v]){
DFS(G, v);
}
}
}
/// @brief /辅助队列
typedef struct{
int data[numVertexes];
int f,r;
}Que;
void InitQueue(Que &Q){
Q.f=Q.r=0;
}
void In(Que &Q,int e){
if ((Q.r+1)%numVertexes==Q.f) return;
Q.data[Q.r]=e;
Q.r=(Q.r+1)%numVertexes;
}
void Out(Que &Q,int &e){
if(Q.f==Q.r) return;
e=Q.data[Q.f];
Q.f=(Q.f+1)%numVertexes;
}
// ------------------------- BFS 广度优先遍历------------------------
// 对连通图进行广度优先遍历
void BFS(MGraph G, int v){
Que Q;
InitQueue(Q); //初始化一辅助用的队列
//把所有结点全部标记为false,表示没有访问过
for(int i=0; i<G.vexnum; i++){
visited[i] = 0;
}
printf("%d",G.Vex[v]);
visited[v]=1;
In(Q,v);
while(Q.f!=Q.r){
Out(Q,v);
//把出队结点的相邻的所有结点入队
for(int w=0; w<G.vexnum; w++){
if(!visited[w] && G.Edge[v][w] != 32767){
printf("%d",G.Vex[w]);
visited[w]=1;
In(Q,w);
}
}
}
}
// 对非连通图的广度遍历
void BFSTraverse(MGraph G){
Que Q;
InitQueue(Q); //初始化一辅助用的队列
int v;
//把所有结点全部标记为false,表示没有访问过
for(v=0; v<G.vexnum; v++){
visited[v] = 0;
}
for(v=0; v<G.vexnum; v++){ //这里是从0开始
//若是未访问过就处理
if(!visited[v]){
printf("%d",G.Vex[v]);
visited[v]=1;
In(Q,v);
while(Q.f!=Q.r){
Out(Q,v);
//把出队结点的相邻的所有结点入队
for(int w=0; w<G.vexnum; w++){
if(!visited[w] && G.Edge[v][w] != 32767){
printf("%d",G.Vex[w]);
visited[w]=1;
In(Q,w);
}
}
}
}
}
}
请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):1 2 5
请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):1 3 1
请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):1 4 6
请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):2 5 3
请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):2 6 4
请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):3 5 3
请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):4 6 2图的顶点为:1 2 3 4 5 6
输出邻接矩阵:
1 2 3 4 5 61 0 5 1 6 ∞ ∞
2 5 0 ∞ ∞ 3 4
3 1 ∞ 0 ∞ 3 ∞
4 6 ∞ ∞ 0 ∞ 2
5 ∞ 3 3 ∞ 0 ∞
6 ∞ 4 ∞ 2 ∞ 0
DFS:125364
BFS:123456
BFS直接遍历(非连通图):123456
1.2有向图
主对角线上数值依然为0。但因为是有向图,所以此矩阵并不对称。
【注意】行是出度
有向图讲究入度与出度,
第i个结点的入度 = 邻接矩阵的第i列的非零元素的个数。(竖着)
第i个结点的出度 = 邻接矩阵的第i行的非零元素的个数。(横着)
第i个结点的度 = 第i行、第i列的非零元素个数之和。
❗邻接矩阵-有向图代码-C
与无向图的区别,仅有在构造的时候:
G->Edge[start-1][end-1] = w;
//有向图不具有对称性
code:
/* 图
邻接矩阵(Adjacency Matrix)
存储方式是用两个数组来表示图。
一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
有向图
C实现
*/
#include <stdio.h>
#include <string.h>
#define MaxVertexNum 100 //顶点数目最大值
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
#define numVertexes 6 // 顶点个数,用于visited数组
#define numEdges 7 // 边个数
typedef struct
{
VertexType Vex[MaxVertexNum]; //顶点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, edgenum; //图的顶点数和弧数
}MGraph;
void create_Graph(MGraph *G);
void create_Graph_ByArray(MGraph *G, int edges[][3]);
void print_Matrix(MGraph G);
void DFS(MGraph G,int v);
void DFSTraverse(MGraph G);
void BFS(MGraph G, int v);
void BFSTraverse(MGraph G);
int main()
{
MGraph G;
// 创建有向图方法1
//create_Graph(&G);
// 创建有向图方法2
//这里可以使用int,因为edge的EdgeType是int
int edges[numEdges][3] = { // 边的起点序号,终点序号,权值
{1,2,5},
{3,1,1},
{4,1,6},
{5,2,3},
{5,3,3},
{6,2,4},
{6,4,2}
};
create_Graph_ByArray(&G,edges);
print_Matrix(G);
printf("\nDFS:");
DFS(G,0);
printf("\nDFS直接遍历(非连通图):");
DFSTraverse(G);
printf("\nBFS:");
BFS(G,0);
printf("\nBFS直接遍历(非连通图):");
BFSTraverse(G);
return 0;
}
// 创建有向图
void create_Graph(MGraph *G){
int i, j;
int start, end; //边的起点序号、终点序号
int w; //边上的权值
// 所创建有向图的顶点数和边数(用空格隔开)。这里也可以输入
G->vexnum = numVertexes;
G->edgenum = numEdges;
printf("\n");
//图的初始化init
for (i=0; i<G->vexnum; i++){
for (j=0; j<G->vexnum; j++){
if (i == j)
G->Edge[i][j] = 0; //结点自身
else
G->Edge[i][j] = 32767; //初始都为表示∞
}
}
//顶点信息存入顶点表
for (i=0; i<G->vexnum; i++){
// printf("请输入第%d个顶点的信息(int):",i+1);
// scanf("%d", &G->Vex[i]);
//这里不输入了,暂时默认0开始
G->Vex[i] = i+1;
}
printf("\n");
//输入有向图边的信息
for (i=0; i<G->edgenum; i++){
printf("请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):");
scanf("%d%d%d", &start, &end, &w);
G->Edge[start-1][end-1] = w;
//有向图不具有对称性
}
}
// 创建有向图
void create_Graph_ByArray(MGraph *G, int edges[][3]){
int i, j;
int start, end; //边的起点序号、终点序号
int w; //边上的权值
// 所创建有向图的顶点数和边数(用空格隔开)。这里也可以输入
G->vexnum = numVertexes;
G->edgenum = numEdges;
printf("\n");
//图的初始化init
for (i=0; i<G->vexnum; i++){
for (j=0; j<G->vexnum; j++){
if (i == j)
G->Edge[i][j] = 0; //结点自身
else
G->Edge[i][j] = 32767; //初始都为表示∞
}
}
//顶点信息存入顶点表
for (i=0; i<G->vexnum; i++){
// printf("请输入第%d个顶点的信息(int):",i+1);
// scanf("%d", &G->Vex[i]);
//这里不输入了,暂时默认0开始
G->Vex[i] = i+1;
}
printf("\n");
// 输入有向图边的信息
for (i=0; i<G->edgenum; i++){
start = edges[i][0];
end = edges[i][1];
w = edges[i][2];
G->Edge[start-1][end-1] = w;
//有向图不具有对称性
}
}
// 输出图
void print_Matrix(MGraph G){
int i, j;
printf("\n图的顶点为:");
for (i=0; i<G.vexnum; i++)
printf("%d ", G.Vex[i]);
printf("\n输出邻接矩阵:\n");
// 横坐标
printf(" "); //表示行坐标,前面空格留给纵坐标
for (i=0; i<G.vexnum; i++)
printf("%5d", G.Vex[i]);
printf("\n");
for (i=0; i<G.vexnum; i++){
// 纵坐标
printf("\n%d", G.Vex[i]);
// 输出邻接矩阵
for (j=0; j<G.vexnum; j++){
if (G.Edge[i][j] == 32767)
printf("%7s", "∞");
else
printf("%5d", G.Edge[i][j]);
}
printf("\n");
}
}
// ------------------------- DFS 深度优先遍历------------------------
int visited[numVertexes]={0};
// 注意:是从0下标开始
void DFS(MGraph G, int x){
// 访问顶点x
printf("%d",G.Vex[x]);
visited[x]=1; //设已访问标记
// 遍历x的邻接顶点
for(int v=0; v<G.vexnum; v++){
//i为x的尚未访问的邻接顶点
if(!visited[v] && G.Edge[x][v] != 32767){
DFS(G, v);
}
}
}
//对非连通图进行深度优先遍历
void DFSTraverse(MGraph G){
//把所有结点全部标记为false,表示没有访问过
for(int v=0; v<G.vexnum; v++){
visited[v] = 0;
}
for(int v=0; v<G.vexnum; v++){ //从v=0开始遍历
if(!visited[v]){
DFS(G, v);
}
}
}
/// @brief /辅助队列
typedef struct{
int data[numVertexes];
int f,r;
}Que;
void InitQueue(Que &Q){
Q.f=Q.r=0;
}
void In(Que &Q,int e){
if ((Q.r+1)%numVertexes==Q.f) return;
Q.data[Q.r]=e;
Q.r=(Q.r+1)%numVertexes;
}
void Out(Que &Q,int &e){
if(Q.f==Q.r) return;
e=Q.data[Q.f];
Q.f=(Q.f+1)%numVertexes;
}
// ------------------------- BFS 广度优先遍历------------------------
// 对连通图进行广度优先遍历
void BFS(MGraph G, int v){
Que Q;
InitQueue(Q); //初始化一辅助用的队列
//把所有结点全部标记为false,表示没有访问过
for(int i=0; i<G.vexnum; i++){
visited[i] = 0;
}
printf("%d",G.Vex[v]);
visited[v]=1;
In(Q,v);
while(Q.f!=Q.r){
Out(Q,v);
//把出队结点的相邻的所有结点入队
for(int w=0; w<G.vexnum; w++){
if(!visited[w] && G.Edge[v][w] != 32767){
printf("%d",G.Vex[w]);
visited[w]=1;
In(Q,w);
}
}
}
}
// 对非连通图的广度遍历
void BFSTraverse(MGraph G){
Que Q;
InitQueue(Q); //初始化一辅助用的队列
int v;
//把所有结点全部标记为false,表示没有访问过
for(v=0; v<G.vexnum; v++){
visited[v] = 0;
}
for(v=0; v<G.vexnum; v++){ //这里是从0开始
//若是未访问过就处理
if(!visited[v]){
printf("%d",G.Vex[v]);
visited[v]=1;
In(Q,v);
while(Q.f!=Q.r){
Out(Q,v);
//把出队结点的相邻的所有结点入队
for(int w=0; w<G.vexnum; w++){
if(!visited[w] && G.Edge[v][w] != 32767){
printf("%d",G.Vex[w]);
visited[w]=1;
In(Q,w);
}
}
}
}
}
}
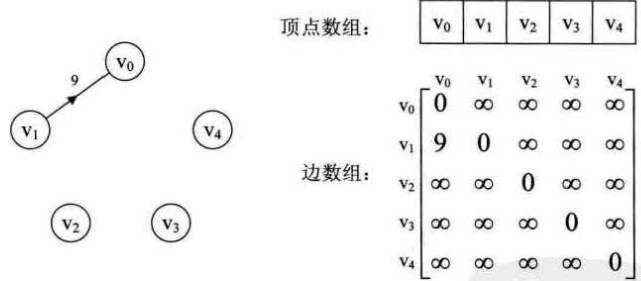
1.3带权图
对于带权图而言,若顶点vi和vj之间有边相连,则邻接矩阵中对应项存放着该边对应的权值。
没有边,那么距离就是无穷。
自己指向自己,那么边就是0。
![A[i][j]](https://img-blog.csdnimg.cn/20210301100252622.png#pic_center)

1.4性能分析
一个一维数组,一个二维数组,存储空间是O(n) + O(n2) = O(n2) ,即O(IVI2)。
邻接矩阵法求顶点的度/出度/入度的时间复杂度为O(IVI)。
适合用于稠密图。
1.5相乘
设图 G 的邻接矩阵为 A(矩阵元素为0/1),则An的元素 An[i][j] 等于由顶点 i 到顶点 j 的长度为 n 的路径的数目。

比如:
A2[1][4]:就是从A->B,然后B->D,这样两次(路径长度为2)的。
A2[1][4] = 1,意思就是满足长度为2的路径,只有一条。
A3同理,表示路径长度为 3 的路径数目。

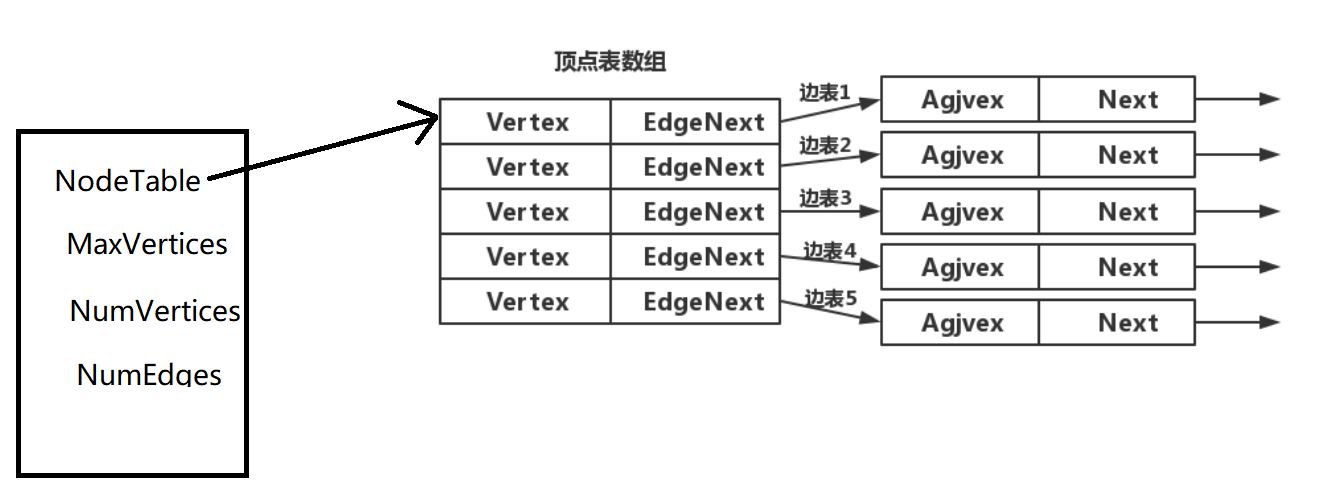
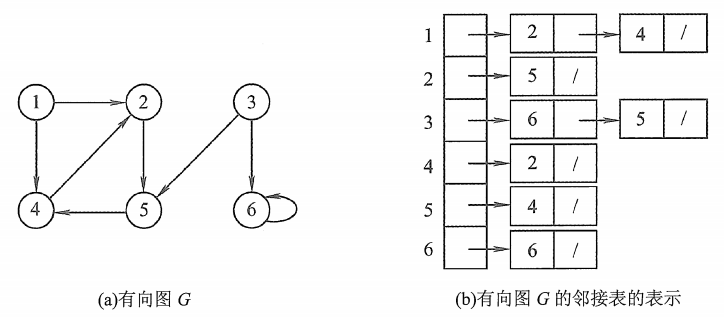
❗2.邻接表
顺序+链式存储
- 不足
当一个图为稀疏图时(边数相对顶点较少),使用邻接矩阵法显然要浪费大量的存储空间,如下图所示:
- 邻接表(Adjacency List)
而图的邻接表法结合了顺序存储 + 链式存储方法,减少了这种不必要的浪费。
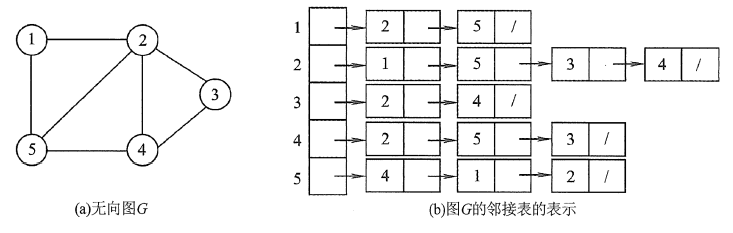
所谓邻接表,是指对图G中的每个顶点 vi 建立一个单链表,第 i 个单链表中的结点表示依附于顶点 vi 的边,这个单链表就称为顶点 vi 的边表。
那么,一个结点的出度就是单链表内的结点个数。
边表的头指针和顶点的数据信息采用顺序存储(称为顶点表),所以在邻接表中存在两种结点:顶点表结点和边表结点,如下图所示:

链表的结点,没有先后顺序,都是直接连在顶点上的。所以链表有很多表示方式,不唯一。
一个参考图:
存储结构定义:
#define MaxVertexNum 100 //顶点数目最大值
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
//边表结点
typedef struct EdgeNode{
int adjvex; //该弧所指向的顶点的下标或者位置
EdgeType weight; //权值,对于非网图可以不需要
struct EdgeNode *next; //指向下一个邻接点
}EdgeNode;
//顶点表结点
typedef struct VertexNode{
VertexType data; //顶点域,存储顶点信息
EdgeNode *firstedge; //边表头指针
}VertexNode, AdjList[MaxVertexNum];
//邻接表
typedef struct{
AdjList adjList;
int vexnum, edgenum; //图的当前顶点数和边数/弧数
}LinkGraph;
2.1无向图
无向图存储中,一条边会出现在两端点的链表中,边结点的数量是2|E|,整体空间复杂度为 O(|V|+ 2|E|)。
2.2有向图
有向图存储中,边结点的数量是|E|,整体空间复杂度为 O(|V|+ |E|)。
❗邻接表-C
/* 图
邻接表(Adjacency List)
存储方式是结合了 顺序存储 + 链式存储方法,减少了邻接矩阵不必要的浪费。
无向图 与 有向图 的区别:就是一条edge是否添加两次到两端节点
这里默认是无向图,但是在代码中注释了有向图
C实现
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MaxVertexNum 100 //顶点数目最大值
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
#define numVertexes 5 // 顶点个数,用于visited数组
#define numEdges 7 // 边个数
//边表结点
typedef struct EdgeNode{
int adjvex; //该弧所指向的顶点的下标或者位置
EdgeType weight; //权值,对于非网图可以不需要
struct EdgeNode *next; //指向下一个邻接点
}EdgeNode;
//顶点表结点
typedef struct VertexNode{
VertexType data; //顶点域,存储顶点信息
EdgeNode *firstedge; //边表头指针
}VertexNode, AdjList[MaxVertexNum];
// AdjList[MaxVertexNum]是静态的链表
//邻接表
typedef struct{
AdjList adjList;
int vexnum, edgenum; //图的当前顶点数和边数/弧数
}LinkGraph;
void create_Graph(LinkGraph *G);
void create_Graph_ByArray(LinkGraph *G, int edges[][3]);
void print_Graph(LinkGraph G);
int main()
{
LinkGraph G;
// 创建图方法1
// create_Graph(&G);
// 创建图方法2
// 这里可以使用int,因为edge的EdgeType是int
int edges[numEdges][3] = { // 边的起点序号,终点序号,权值
{1,2,1},
{1,5,1},
{2,3,1},
{2,4,1},
{2,5,1},
{3,4,1},
{4,5,1}
};
create_Graph_ByArray(&G,edges);
print_Graph(G);
return 0;
}
// 创建图
void create_Graph(LinkGraph *G){
int i, j;
int start, end; //边的起点序号、终点序号
int w; //边上的权值
// 所创建图的顶点数和边数(用空格隔开)。这里也可以输入
G->vexnum = numVertexes;
G->edgenum = numEdges;
printf("\n");
//初始化顶点
for (i=0; i<G->vexnum; i++){
G->adjList[i].data = i+1; //顶点初始化
G->adjList[i].firstedge = NULL; //边表头指针初始化为空
}
//初始化边
for (i=0; i<G->edgenum; i++){
printf("请输入边的起点序号,终点序号,权值(用空格隔开)(int,从1开始,没有0):");
scanf("%d%d%d", &start, &end, &w);
// 创建边表结点
// 有向图,只需要创建一个结点
EdgeNode *e = (EdgeNode*)malloc(sizeof(EdgeNode));
e->adjvex = end-1; //终点序号
e->weight = w;
//将结点e插入顶点表start的边表中
e->next = G->adjList[start-1].firstedge;
G->adjList[start-1].firstedge = e;
// 无向图,还要插入终点序号的边表
//创建边表结点
EdgeNode *e_ = (EdgeNode*)malloc(sizeof(EdgeNode));
e_->adjvex = start-1; //起点序号
e_->weight = w;
//将结点e_插入顶点表end的边表中
e_->next = G->adjList[end-1].firstedge;
G->adjList[end-1].firstedge = e_;
}
}
// 使用数组创建图
void create_Graph_ByArray(LinkGraph *G, int edges[][3]){
int i, j;
int start, end; //边的起点序号、终点序号
int w; //边上的权值
// 所创建图的顶点数和边数(用空格隔开)。这里也可以输入
G->vexnum = numVertexes;
G->edgenum = numEdges;
printf("\n");
//初始化顶点
for (i=0; i<G->vexnum; i++){
G->adjList[i].data = i+1; //顶点初始化
G->adjList[i].firstedge = NULL; //边表头指针初始化为空
}
//初始化边
for (i=0; i<G->edgenum; i++){
start = edges[i][0];
end = edges[i][1];
w = edges[i][2];
// 创建边表结点
// 有向图,只需要创建一个结点
EdgeNode *e = (EdgeNode*)malloc(sizeof(EdgeNode));
e->adjvex = end-1; //终点序号
e->weight = w;
//将结点e插入顶点表start的边表中
e->next = G->adjList[start-1].firstedge;
G->adjList[start-1].firstedge = e;
// 无向图,还要插入终点序号的边表
//创建边表结点
EdgeNode *e_ = (EdgeNode*)malloc(sizeof(EdgeNode));
e_->adjvex = start-1; //起点序号
e_->weight = w;
//将结点e_插入顶点表end的边表中
e_->next = G->adjList[end-1].firstedge;
G->adjList[end-1].firstedge = e_;
}
}
// 输出图
void print_Graph(LinkGraph G){
int i, j;
printf("\n图的顶点为:");
for (i=0; i<G.vexnum; i++){
printf("%d ", G.adjList[i].data);
}
// 输出邻接表
printf("\n图的邻接矩阵为:\n");
for (i=0; i<G.vexnum; i++){ //遍历顶点
printf("%d. %d:> ",i, G.adjList[i].data); //输出顶点
EdgeNode *p = G.adjList[i].firstedge; //边结构
while (p){ //遍历边
printf("%d-->", p->adjvex+1);
p = p->next;
}
printf("Null.\n");
}
}
图的顶点为:1 2 3 4 5
图的邻接矩阵为:
- 1:> 5–>2–>Null.
- 2:> 5–>4–>3–>1–>Null.
- 3:> 4–>2–>Null.
- 4:> 5–>3–>2–>Null.
- 5:> 4–>2–>1–>Null.
邻接矩阵VS邻接表
| 邻接矩阵 | 邻接表 | |
|---|---|---|
| 空间复杂度 | O( IVI2 ) | 无向图O(|V|+2|E|); 有向图O(|V|+|E|)。 |
| 适用于 | 稠密图 | 稀疏图 |
| 表示方式 | 唯一 | 不唯一 |
| 计算度、出度、入度 | 必须遍历对应的行或列 | 计算有向图的度、入度不方便,其余很方便。 |
| 找相邻的边 | 必须遍历对应的行或列 | 找有向图的入边不方便,其余很方便。 |
| 删除边、结点 | 删除边很方便,删除结点要移动大量数据 | 删除边、结点都不方便 |
邻接矩阵
- 在简单应用中,可直接用二维数组作为图的邻接矩阵(顶点信息等均可省略)。
- 当邻接矩阵中的元素仅表示相应的边是否存在时,EdgeType可定义为值为0和1的枚举类型或者bool。
- 无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可采用压缩存储。
- 邻接矩阵表示法的空间复杂度为O(n2),其中n为图的顶点数|V|。
- 用邻接矩阵法存储图,很容易确定图中任意两个顶点之间是否有边相连。但是,要确定图中有多少条边,则必须按行、按列对每个元素进行检测,所花费的时间代价很大。
- 稠密图适合使用邻接矩阵的存储表示。
邻接表
-
对于稀疏图,采用邻接表表示将极大地节省存储空间。
-
在邻接表中,给定一顶点,能很容易地找出它的所有邻边,因为只需要读取它的邻接表。在邻接矩阵中,相同的操作则需要扫描一行,花费的时间为O(n)。
但是,若要确定给定的两个顶点间是否存在边,则在邻接矩阵中可以立刻查到,而在邻接表中则需要在相应结点对应的边表中查找另一结点,效率较低。 -
在有向图的邻接表表示中,
求一个给定顶点的出度只需计算其邻接表中的结点个数;
但求其顶点的入度则需要遍历全部的邻接表。因此,也有人采用逆邻接表的存储方式来加速求解给定顶点的入度。当然,这实际上与邻接表存储方式是类似的。
-
图的邻接表表示并不唯一,因为在每个顶点对应的单链表中,各边结点的链接次序可以是任意的,它取决于建立邻接表的算法及边的输入次序。