【数模修炼之旅】02 多目标规划 深度解析（教程+代码）

接下来 C君将会用至少30个小节来为大家深度解析数模领域常用的算法，大家可以关注这个专栏，持续学习哦，对于大家的能力提高会有极大的帮助。

1 多目标规划介绍及应用

求解多目标线性规划的基本思想大都是将多目标问题转化为单目标规划，在比赛中经常会用到。本文只介绍一种最常用方法。大家可以去搜搜一些其他的多目标规划方法：理想点法、线性加权和法、最大最小法、目标规划法。

具体的，多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。又称多目标最优化。通常记为 MOP(multi-objective programming)。

多目标规划的概念是 1961年由美国数学家查尔斯和库柏首先提出的。多目标最优化思想，最早是在1896年由法国经济学家V.帕雷托提出来的。他从政治经济学的角度考虑把本质上是不可比较的许多目标化成单个目标的最优化问题，从而涉及了多目标规划问题和多目标的概念。

模型具体为：

多目标线性规划有着两个和两个以上的目标函数,且目标函数和约束条件全是线性函数,其数学模型表示为：

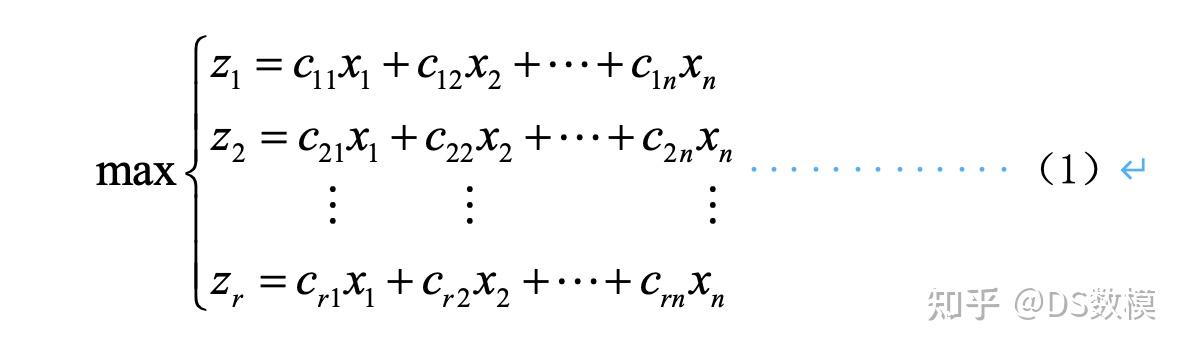
约束条件为：

2 多目标规划的过程详解

2.1 分析和计算步骤

多目标规划（Multi-Objective Optimization）涉及同时优化多个目标函数，这些目标函数通常是相互矛盾的。分析和计算步骤可以分为几个主要阶段：

1. 问题定义

• 确定目标函数：识别需要优化的多个目标函数。例如，最大化利润和最小化成本。
• 确定决策变量：识别影响目标函数的变量。这些变量是可以控制的因素。
• 设定约束条件：定义决策变量必须满足的约束条件，如资源限制、技术限制等。

2. 建立数学模型

• 目标函数：设定目标函数的数学形式，通常是目标函数的集合，例如
  
  。
• 约束条件：设定约束条件的数学形式，通常是线性或非线性的约束，例如
  
  和
  
  。

3. 选择优化方法

• 权重法：将多个目标函数转化为一个单一的目标函数，通过给每个目标函数分配权重。例如：
   
• ε-约束法：选择一个目标函数进行优化，将其他目标函数作为约束条件。例如：
   
• Pareto优化：寻找 Pareto 最优解，这是一种不可以在某个目标上改进而不在其他目标上恶化的解。常用的方法有遗传算法、多目标粒子群优化等。

4. 求解优化问题

• 求解算法：选择合适的优化算法（如线性规划、整数规划、遗传算法、模拟退火等）来求解多目标规划问题。
• 计算Pareto前沿：使用算法计算所有的 Pareto 最优解，得到 Pareto 前沿，显示不同目标之间的权衡。

5. 分析和选择

• Pareto前沿分析：分析 Pareto 前沿中的解，理解不同解决方案之间的权衡关系。
• 决策：根据实际需求选择一个最合适的解决方案，可能需要考虑非技术因素，如成本、时间、资源等。

6. 验证和实施

• 验证：验证所选择的解决方案是否满足所有的约束条件，并且在实践中是否可行。
• 实施：将最终选择的解决方案付诸实践，并进行必要的调整和优化。

7. 反馈和调整

• 监控：实施过程中监控解决方案的实际表现。
• 调整：根据实际情况对模型和方案进行必要的调整和改进。

这些步骤为多目标规划提供了一个系统的分析框架，帮助决策者在多个目标之间做出平衡和优化决策。

3 多目标规划代码（lingo+matlab+python）

现在给一个例子，然后用两种代码进行求解：

例子：

3.1 lingo代码：

序贯算法中每个单目标问题都是一个线性规划问题, 可以使用Lingo软件进行求解。

以上例为例，利用lingo求解如下：

第一级：

 model:
 sets:
 variable/1,2/:x;
 s_con_num/1..4/:g,dplus,dminus; !目标约束项数;
 s_con(s_con_num,variable):c;
 !dplus=d+,dminus=d-,目标约束系数c=c(i,j);
 endsets
 data:
 g=1500 0 16 15;c=200 300 2 -1 4 0 0 5; !默认按行赋值;
 enddata
 min=dminus(1); !一级目标函数;
 2*x(1)+2*x(2)<=12;
 @for(s_con_num(i):@sum(variable(j):c(i,j)*x(j)+dminus(i)-dplus(i))=g(i););
 @for(variable:@gin(x)); !变量取整约束;
 end

第二级：

 model:
 sets:
 variable/1,2/:x;
 s_con_num/1..4/:g,dplus,dminus;
 s_con(s_con_num,variable):c;
 endsets
 data:
 g=1500 0 16 15;c=200 300 2 -1 4 0 0 5;
 enddata
 min=dplus(2)+dminus(2); !二级目标函数;
 2*x(1)+2*x(2)<=12;
 @for(s_con_num(i):@sum(variable(j):c(i,j)*x(j)+dminus(i)-dplus(i))=g(i););
 dminus(1)=0; !一级目标约束;
 @for(variable:@gin(x));
 end
 ​

第三级：

 model:
 sets:
 variable/1,2/:x;
 s_con_num/1..4/:g,dplus,dminus;
 s_con(s_con_num,variable):c;
 endsets
 data:
 g=1500 0 16 15;c=200 300 2 -1 4 0 0 5;
 enddata
 min=3*dplus(3)+3*dminus(3)+dplus(4); !三级目标函数;
 2*x(1)+2*x(2)<=12;
 @for(s_con_num(i):@sum(variable(j):c(i,j)*x(j))+dminus(i)-dplus(i)=g(i););
 dminus(1)=0;dplus(2)+dminus(2)=0; !一、二级目标约束;
 @for(variable:@gin(x));
 end
 ​

三个阶段一起：

 model:
 sets:
 level/1..3/:p,z,goal; !三个目标;
 variable/1,2/:x;
 s_con_num/1..4/:g,dplus,dminus;
 s_con(s_con_num,variable):c;
 h_con_num/1/:b;
 h_con(h_con_num,variable):a;
 obj(level,s_con_num)/1 1,2 2,3 3,3 4/:wplus,wminus; !权重;
 endsets
 data:
 ctr=?;
 goal=? ? 0;
 b=12;
 a=2 2;
 g=1500 0 16 15;
 c=200 300 2 -1 4 0 0 5;
 wplus=0 1 3 1;
 wminus=1 1 3 0;
 enddata
 min=@sum(level:p*z);
 @for(level(i)|i#ne#ctr:p(i)=0);
 @for(level(i):z(i)=@sum(obj(i,j):wplus(i,j)*dplus(j)+wminus(i,j)*dminus(j)););
 @for(h_con_num(i):@sum(variable(j):a(i,j)*x(j))<=b(i););
 @for(s_con_num(i):@sum(variable(j):c(i,j)*x(j))+dminus(i)-dplus(i)=g(i););
 @for(level(i)|i#lt#@size(level):@bnd(0,z(i),goal(i)));
 @for(variable:@gin(x));
 end
 ​

3.2 matlab代码：

fgoalattain()函数的用法： x = fgoalattain(fun,x0,goal,weight) x = fgoalattain(fun,x0,goal,weight,A,b) x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq) x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub) x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon) x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options) x = fgoalattain(problem) [x,fval] = fgoalattain() [x,fval,attainfactor,exitflag,output] = fgoalattain() [x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(___)

例：求解多目标线性规划问题

定义目标函数：

 function F=Fun16_5(x)
 F=[-100*x(1)-90*x(2)-80*x(3)-70*x(4);3*x(2)+2*x(4)];
 end
 ​

goal由两个目标函数分别求出目标值合并而成;weight由abs(goal)取定

 a=[-1 -1 0 0;0 0 -1 -1;3 0 2 0;0 3 0 2]
 b=[-30,-30,120,48].'
 c1=-[100,90,80,70]
 c2=[0,3,0,2]
 [x1,goal1]=linprog(c1,a,b,[],[],zeros(4,1))
 [x2,goal2]=linprog(c2,a,b,[],[],zeros(4,1))
 goal=[goal1;goal2]
 [x,fval]=fgoalattain('Fun16_5',rand(4,1),goal,abs(goal),a,b,[],[],zeros(4,1))
 ​

3.3 python代码

在 Python 中实现多目标规划可以使用一些优化库，如 scipy.optimize、pyomo、pymoo等。以下是一些示例代码，展示了如何使用不同的库来处理多目标规划问题。

示例 1: 使用 pymoo 库

pymoo 是一个专门用于多目标优化的库。以下代码展示了如何使用 pymoo 解决一个简单的多目标优化问题：

 from pymoo.optimize import minimize
 from pymoo.core.problem import Problem
 from pymoo.core.variable import Real
 from pymoo.algorithms.moo.nsga2 import NSGA2
 from pymoo.visualization.scatter import Scatter
 import numpy as np
 ​
 # 定义问题
 class MyProblem(Problem):
     def __init__(self):
         super().__init__(n_var=2, n_obj=2, n_constr=0, xl=np.array([0, 0]), xu=np.array([5, 5]))
         
     def _evaluate(self, x, out, *args, **kwargs):
         f1 = x[:, 0]**2 + x[:, 1]**2
         f2 = (x[:, 0] - 1)**2 + (x[:, 1] - 1)**2
         out["F"] = np.column_stack([f1, f2])
 ​
 # 创建问题实例
 problem = MyProblem()
 ​
 # 使用 NSGA-II 算法
 algorithm = NSGA2(pop_size=100)
 ​
 # 进行优化
 result = minimize(problem,
                   algorithm,
                  ('n_gen', 50),
                   seed=1,
                   verbose=True)
 ​
 # 可视化 Pareto 前沿
 Scatter().add(result.F).show()
 ​

示例 2: 使用 scipy.optimize 进行加权和的方法

虽然 scipy.optimize 主要用于单目标优化，但你可以通过加权和的方法将多目标问题转化为单目标问题：

 from scipy.optimize import minimize
 ​
 # 目标函数
 def objective(x, weights):
    f1 = x[0]**2 + x[1]**2
    f2 = (x[0] - 1)**2 + (x[1] - 1)**2
    return weights[0] * f1 + weights[1] * f2
 ​
 # 初始点
 x0 = [0, 0]
 ​
 # 权重
 weights = [0.5, 0.5]
 ​
 # 约束条件
 def constraint(x):
    return 5 - (x[0] + x[1])
 ​
 cons = [{'type': 'ineq', 'fun': constraint}]
 ​
 # 最优化
 result = minimize(objective, x0, args=(weights,), constraints=cons, method='SLSQP')
 ​
 print("Optimal solution:", result.x)
 print("Objective function value:", result.fun)
 ​

需要参加数模竞赛的同学，可以看我的这个名片，会有最新的助攻哦：（大型比赛前会对名片进行更新）