信息论在机器学习中的实际应用

一、说明

二、什么是信息论？

2.1 信息论中的关键概念

2.2 熵与信息

2.3 相互信息

2.4 Kullback-Leibler 背离

三、信息论在机器学习中的应用

3.1 功能选择：

3.2 计算边际概率分布

3.3 决策树：Information 增益

3.4 评估具有 KL 背离的概率模型：

四、神经网络：交叉熵损失

一、说明

数据工具的格局在不断变化。每天都会引入新的库和工具，但它们都依赖于基本的数学概念。至关重要的是，要优先考虑理解这些概念，而不是专注于单个工具。

如作为一名数据科学家，你可能经常听到“信息论”这个词在机器学习的背景下出现。但究竟什么是信息论，为什么它对机器学习如此重要？在本文中，我们将探讨信息论的基础知识、其关键概念，以及它如何以简单而翔实的方式应用于机器学习。

二、什么是信息论？

信息论是应用数学的一个分支，它对信息进行量化。克劳德·香农（Claude Shannon）在他1948年的开创性论文《通信的数学理论》（A Mathematical Theory of Communication）中介绍了它。信息论为理解信息如何被测量、传输和处理提供了一个框架。

2.1 信息论中的关键概念

以下是信息论中与机器学习特别相关的一些基本概念：

熵与信息

相互信息

KL背离

2.2 熵与信息

熵是数据集中不确定性或随机性的度量。在机器学习中，熵通常用于量化随机变量的不可预测性。简单来说，它衡量的是随机变量的每个值平均产生多少“信息”。较高的熵意味着更大的不确定性，而较低的熵表明更多的可预测性。离散随机变量（ X ）的熵（ H ）的公式，具有可能的结果（ x₁， x₂， ...， xn ）和概率（ P（x₁）， P（x₂）， ...， P（xn））由下式给出：

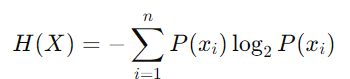
该公式源自信息与事件概率成反比的概念。使用对数以 2 为底的原因是，我们通常以位为单位测量信息。

熵公式从何而来？

首先，我们需要量化单个事件的信息内容。概率为P（习）的事件习的信息内容（也称为自信息）定义为：

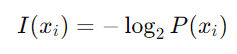
对数：使用对数是因为它们具有与我们对信息的直观理解非常一致的属性。例如，概率乘积的对数转换为对数之和，反映了信息内容的累加性。
以 2 为基数：使用以 2 为基数的对数，因为我们通常以比特为单位测量信息。在其他上下文中，可能会使用不同的基数（如自然对数），但在信息论中，基数 2 是标准的。
双边投资条约是信息的基本计量单位。术语“位”代表二进制数字，它表示单个二进制决策或在两个相同可能的结果（通常表示为 0 和 1）之间的选择可以存储的信息量。

概率：P（是）=0.5，P（否）=0.5

“是”和“否”携带相同数量的信息（比特）

概率：P（是）=0.9，P（否）=0.1

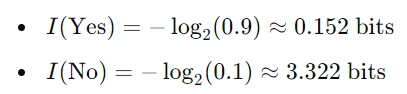
“否”现在带有更多信息（更多位），因为它不太可能发生。

非负性：信息内容始终是非负的，因为概率在 0 到 1 之间。
可能性较小的事件的信息含量越高：事件的可能性越小，其信息含量就越高。例如，一个罕见的事件发生时会携带更多信息。

预期信息内容（熵）： 熵是随机变量 X 的所有可能事件（结果）的预期（平均）信息内容。为了计算这一点，我们取每个事件的信息内容的概率加权和：

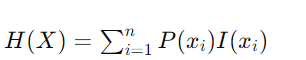
对于公平的硬币：

扬程：P（扬程）=1/2
尾部：P（Tails）=1/2

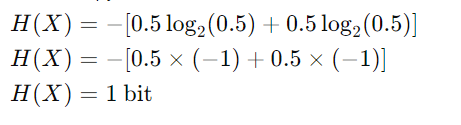
假设我们有一个有偏见的硬币，其概率如下：

列出结果及其概率：

头数：P（Heads）=0.7
尾部：P（Tails）=0.3

应用熵公式：

对于磁头：P（磁头）log₂P（磁头）=0.7log₂0.7
对于尾部：P（tails）log₂P（tails）=0.3log₂0.3

对结果求和：

H（X）=−（0.7log₂0.7+0.3log₂0.3）

log₂0.7≈−0.514
log₂0.3≈−1.737

插入以下值：

H（X）=0.3598+0.5211

水平（X）≈0.881

因此，这种偏置硬币翻转的熵 H（X）约为 0.881 位。

0.881 比特的熵意味着平均而言，每次抛硬币提供约 0.881 比特的信息。这小于 1 比特，因为硬币偏向正面，使结果比公平的硬币（熵为 1 比特）更可预测。

2.3 相互信息

互信息衡量一个随机变量包含的关于另一个随机变量的信息量。它有助于理解变量之间的依赖关系。互信息的公式：

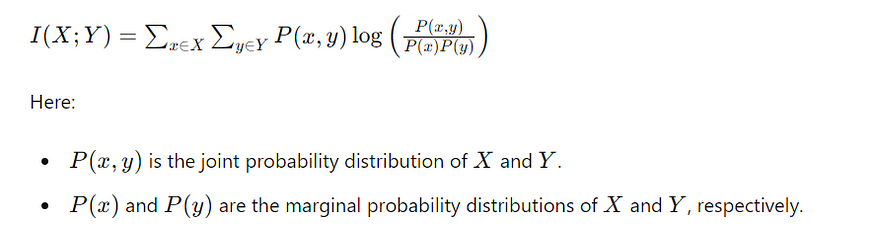
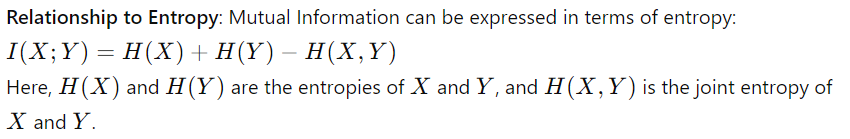
2.4 Kullback-Leibler 背离

也称为 KL 散度，它衡量两个概率分布之间的差异。它在机器学习中被广泛用于将数据的真实分布与预测的分布进行比较。KL背离的公式为：

KL 散度可以解释为使用针对 Q 优化的代码而不是针对 P 优化的代码对来自 P 的样本进行编码所需的预期额外比特数。它量化了当真实分布为 P 时假设分布 Q 的低效率。

三、信息论在机器学习中的应用

信息论在机器学习中有着广泛的应用，从特征选择到模型评估。以下是它发挥关键作用的几个关键领域：

3.1 功能选择：

在机器学习中，选择正确的特征对于构建有效的模型至关重要。信息论有助于通过互信息识别信息量最大的特征。通过选择与目标变量具有高度互信息的特征，我们可以提高模型的性能。

互信息如何帮助特征选择？

I. 量化特征相关性：

互信息衡量一个特征对预测目标变量的贡献信息量。互信息分数较高的特征对模型的信息量更大，相关性更强。
通过根据特征与目标变量的互信息对特征进行排序，我们可以确定要包含在模型中的最重要的特征。

二、非线性关系的处理：

与衡量线性关系的相关性不同，互信息可以捕获任何类型的依赖关系，包括非线性关系。这使其成为更灵活、更强大的特征选择工具。

III. 抗扩展性：

互信息不受变量尺度的影响，使其成为各种数据集中特征选择的稳健度量。

例：

让我们考虑一个具有以下特征的数据集：年龄、收入和购买（目标变量，指示一个人是否进行了购买）。我们的目标是确定哪个特征（年龄或收入）对于预测购买情况更有帮助。

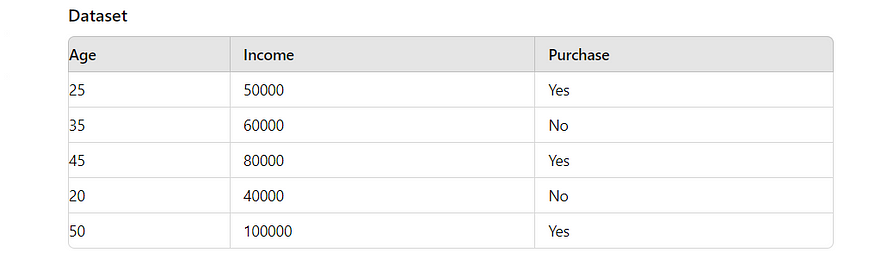
计算联合概率分布

首先，我们需要计算 Age and Purchase 和 Income and Purchase 的联合概率分布。

年龄和购买的联合概率分布

计算 Age 和 Purchase 的每个组合的出现次数。
除以观测值总数可得到联合概率。

例：

P（年龄=25，购买=是）=1/5
P（年龄=35，购买=否）=1/5

收入和购买的联合概率分布

计算 Income 和 Purchase 的每个组合的出现次数。
除以观测值总数可得到联合概率。

例：

P（收入=50000，购买=是）=1/5
P（收入=60000，购买=否）=1/5

同样，计算其他组合。

3.2 计算边际概率分布

接下来，我们需要计算年龄、收入和购买的边际概率。

年龄的边际概率

P（年龄=25）=1/5
P（年龄=35）=1/5

同样，计算其他年龄。

收入的边际概率

P（收入=50000）=1/5
P（收入=60000）=1/5

同样，计算其他收入。

边际购买概率

P（购买=是）=3/5
P（购买=否）=2/5

计算互信息

使用联合概率和边际概率，我们可以计算互信息。

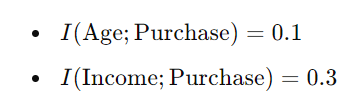
这些结果表明，与年龄相比，收入与购买的相互信息更高。这意味着“收入”对于预测一个人是否会进行购买提供更多信息。

Python 中的 SKLEARN 库提供了一种通过模块使用互信息执行特征选择的便捷方法。feature_selection



import pandas as pd
from sklearn.feature_selection import mutual_info_classif

# Sample dataset
data = {
    'Age': [25, 35, 45, 20, 50],
    'Income': [50000, 60000, 80000, 40000, 100000],
    'Purchase': ['Yes', 'No', 'Yes', 'No', 'Yes']
}

# Create a DataFrame
df = pd.DataFrame(data)

# Encode the target variable
df['Purchase'] = df['Purchase'].map({'Yes': 1, 'No': 0})

# Separate features and target variable
X = df[['Age', 'Income']]
y = df['Purchase']

# Calculate mutual information
mi = mutual_info_classif(X, y)

# Create a DataFrame to display results
mi_df = pd.DataFrame(mi, index=X.columns, columns=["Mutual Information"])
print(mi_df)

3.3 决策树：Information 增益

熵是构建决策树时使用的基本概念。该算法在每个节点上分割数据，以最小化熵（或最大化信息增益），从而产生更高效、更准确的模型。特征（A）上的分割的信息增益（IG）计算公式为：

为了理解信息增益公式的推导，我们需要经历涉及熵计算的几个步骤。

目标变量的熵：目标变量 Y 的熵衡量与 Y 相关的不确定性。它由下式给出

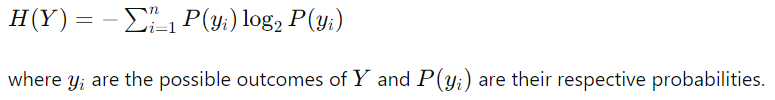
条件熵：条件熵 H（Y∣X）在我们知道另一个变量 X 的值的情况下衡量 Y 的不确定性。它的计算公式为：

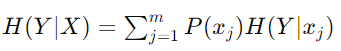
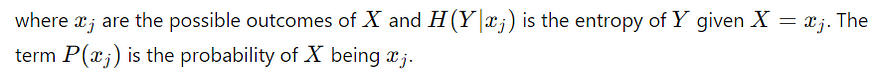
信息增益是给定 X 的 Y 的熵和 Y 的条件熵之间的差值。它表示观察 X 后 Y 的不确定性减少。

这个公式告诉我们，知道属性 X 可以降低目标变量 Y 的不确定性。

例：

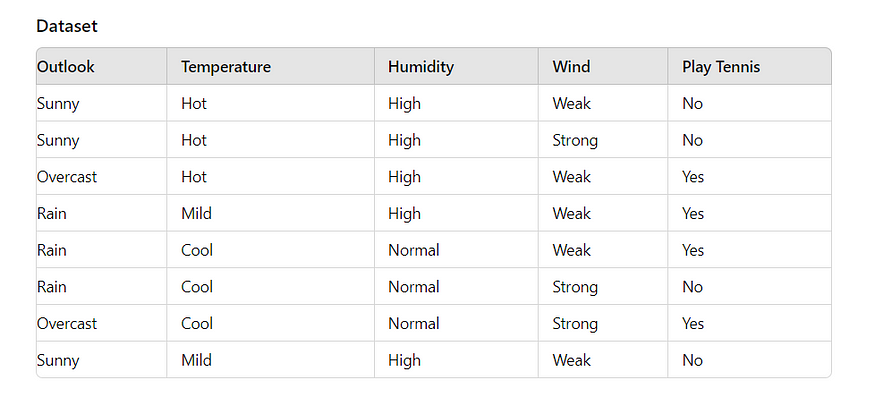
I. 计算目标变量的熵

二、计算条件熵：

条件熵衡量给定属性的目标变量的不确定性。对于属性“Outlook”：

计算“Outlook”的每个值的熵：

对于 Sunny：

子集：[否，否，否]
熵：H（Sunny）=0，因为所有结果均为“否”。

对于阴天：

子集：[是，是]
熵：H（阴天）=0，因为所有结果都是“是”。

对于雨：

子集：[是，是，否]
概率P（是）=2/3;P（否）=1/3
熵：

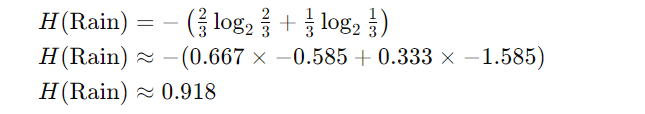
计算条件熵的加权平均值：

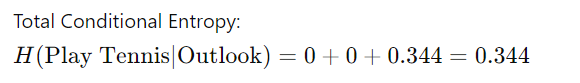
三、信息增益的计算

信息增益是考虑属性后熵的减少。信息增益的公式为：

属性“Outlook”的信息增益为 0.610。这个值表明了解“展望”可以减少是否打网球的不确定性。更高的信息增益意味着该属性对于在决策树中做出决策更有用。您可以对其他属性重复此过程，以确定哪个属性具有最高的信息增益，因此最适合分割数据。

Python 代码：

import numpy as np
import pandas as pd

# Sample dataset
data = {
    'Outlook': ['Sunny', 'Sunny', 'Overcast', 'Rain', 'Rain', 'Rain', 'Overcast', 'Sunny'],
    'Temperature': ['Hot', 'Hot', 'Hot', 'Mild', 'Cool', 'Cool', 'Cool', 'Mild'],
    'Humidity': ['High', 'High', 'High', 'High', 'Normal', 'Normal', 'Normal', 'High'],
    'Wind': ['Weak', 'Strong', 'Weak', 'Weak', 'Weak', 'Strong', 'Strong', 'Weak'],
    'Play Tennis': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No']
}

# Create a DataFrame
df = pd.DataFrame(data)

# Function to calculate entropy
def entropy(target_col):
    elements, counts = np.unique(target_col, return_counts=True)
    entropy = np.sum([(-counts[i]/np.sum(counts)) * np.log2(counts[i]/np.sum(counts)) for i in range(len(elements))])
    return entropy

# Function to calculate information gain
def info_gain(data, split_attribute_name, target_name="Play Tennis"):
    # Calculate the entropy of the total dataset
    total_entropy = entropy(data[target_name])
    
    # Calculate the values and the corresponding counts for the split attribute
    vals, counts= np.unique(data[split_attribute_name], return_counts=True)
    
    # Calculate the weighted entropy
    weighted_entropy = np.sum([(counts[i]/np.sum(counts)) * entropy(data.where(data[split_attribute_name]==vals[i]).dropna()[target_name]) for i in range(len(vals))])
    
    # Calculate the information gain
    information_gain = total_entropy - weighted_entropy
    return information_gain

# Calculate the information gain for the attribute 'Outlook'
info_gain_outlook = info_gain(df, 'Outlook')
print(f'Information Gain for Outlook: {info_gain_outlook}')

# You can calculate information gain for other attributes similarly
info_gain_temperature = info_gain(df, 'Temperature')
info_gain_humidity = info_gain(df, 'Humidity')
info_gain_wind = info_gain(df, 'Wind')

print(f'Information Gain for Temperature: {info_gain_temperature}')
print(f'Information Gain for Humidity: {info_gain_humidity}')
print(f'Information Gain for Wind: {info_gain_wind}')

3.4 评估具有 KL 背离的概率模型：

KL 背离通常用于评估机器学习模型，尤其是在概率模型的背景下。它有助于衡量预测概率与实际数据分布的匹配程度。KL 散度越小，表明模型拟合越好。

例：

考虑一个简单的例子，我们有一个真实的分布 P 和一个模型的估计分布 Q：

真分布P：P（x）=[0.2,0.5,0.3]
估计分布Q：Q（x）=[0.1,0.6,0.3]

要计算 KL 背离：

此结果表明真实分布与模型的估计分布之间存在很小的差异，表明模型的预测相对接近真实分布。

KL 背离可以用作机器学习算法中的正则化术语。通过对 KL 与先前分布背离度较高的模型进行惩罚，它有助于防止过拟合，并鼓励更简单、更普遍的模型。

四、神经网络：交叉熵损失

交叉熵损失，也称为对数损失，量化真实标签和预测概率之间的差异。

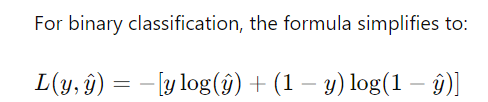
交叉熵与熵有什么关系？

Cross-Entropy 使用模型（或近似）分布 Q 量化对分布 P 中的数据进行编码所需的平均比特数。之前，我提到了 Kullback-Leibler （KL）散度，它衡量假设分布 Q 而不是真实分布 P 的低效率。通过结合 KL 散度和熵，将计算交叉熵。

交叉熵结合了固有的不确定性（熵）和近似的低效率（KL散度），表示使用模型分布Q编码真实分布P所需的总比特数。

为什么我们使用交叉熵损失？

在神经网络的上下文中，交叉熵损失用于：

惩罚错误的预测，奖励正确的预测。
在训练期间指导优化过程。

交叉熵损失随着预测概率与实际标签的差异而增加。以下是其行为的细分：

正确预测：当预测的概率接近真实标签时，损失很小。
错误预测：当预测的概率与真实标签相去甚远时，损失很大。

损失函数被设计为在训练期间最小化，这提高了模型预测的准确性。

交叉熵损失在神经网络中的应用

在训练过程中，神经网络会对每个数据点进行预测。计算预测概率和真实标签之间的交叉熵损失。优化器调整网络的权重以最小化交叉熵损失。
在多类分类中，交叉熵损失通常与softmax激活函数结合使用。Softmax 将网络的原始输出分数转换为总和为 1 的概率。

import numpy as np

# Define the true and model distributions
P = np.array([0.8, 0.2])
Q = np.array([0.7, 0.3])

# Calculate Entropy H(P)
entropy_P = -np.sum(P * np.log2(P))
print(f"Entropy H(P): {entropy_P:.3f}")

# Calculate Cross-Entropy H(P, Q)
cross_entropy_PQ = -np.sum(P * np.log2(Q))
print(f"Cross-Entropy H(P, Q): {cross_entropy_PQ:.3f}")

# Calculate KL Divergence D_KL(P || Q)
kl_divergence_PQ = np.sum(P * np.log2(P / Q))
print(f"KL Divergence D_KL(P || Q): {kl_divergence_PQ:.3f}")

# Verify the relationship H(P, Q) = H(P) + D_KL(P || Q)
print(f"Verification H(P, Q) == H(P) + D_KL(P || Q): {np.isclose(cross_entropy_PQ, entropy_P + kl_divergence_PQ)}")
>>
Entropy H(P): 0.722
Cross-Entropy H(P, Q): 0.829
KL Divergence D_KL(P || Q): 0.107
Verification H(P, Q) == H(P) + D_KL(P || Q): True

总之，信息论为理解和改进机器学习模型提供了一个强大的工具包。数据科学家可以通过利用熵、互信息和 KL 散度等概念来构建更高效、准确和可解释的模型。无论是进行特征选择、构建决策树，还是评估模型性能，扎实掌握信息理论都可以显着提高一个人的分析能力和决策过程。

参考：

拉扬·亚斯明