今天小编在学习 PyTorch 时,突然发现咋每次运行所得损失绘制的曲线都不一样呢？即使小编使用torch.manual_seed()函数固定 torch 的随机数种子每次运行的结果还是不一样，因此小编就写一篇文章记录一下。

数据集

本次使用的数据集是小编自定义的小型数据集：

x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	y
46	41	13	57	21	42	22	44	54	32	1
39	55	19	56	23	51	30	30	35	56	0
42	33	14	35	29	53	30	51	33	59	1
51	25	18	23	27	28	24	39	21	30	0
36	58	20	42	26	49	28	51	21	36	1
60	30	16	41	26	58	28	23	26	41	1
28	26	12	58	23	46	51	41	54	27	0
45	37	10	50	26	26	27	27	32	54	1
47	49	16	37	20	49	20	37	44	28	0
46	55	12	59	26	38	22	20	43	56	1
56	27	13	26	20	26	45	26	53	34	1

注：

1. 表格中xi 表示样本特征（输入），而y表示值（输出）。
2. 制作数据集时，需要先将样本数据导入excel表格，再将文件保存为.csv格式的文件，最后再使用函数np.loadtxt(DATASETS_PATH + “文件名.csv”, delimiter=“,”, dtype=np.float32, skiprows=1)即可完成数据导入。

源码与分析

首先使用 numpy 加载数据集，并且将模型的输入与输出值分别取出。

def dataLoader():
    """
    加载数据集
    """
    xy = np.loadtxt(DATASETS_PATH + "/my_test/my_test.csv", delimiter=",", dtype=np.float32, skiprows=1)
    x_data = torch.from_numpy(xy[:, :-1])
    y_data = torch.from_numpy(xy[:, [-1]])

    return x_data, y_data

定义模型，在这个模型的最初输入是 10 维数据，输出是 1 维数据。

class my_model(nn.Module):
    def __init__(self):
        super(my_model, self).__init__()
        self.network = nn.Sequential(
            nn.Linear(10, 5),
            nn.ReLU(),
            nn.Linear(5, 2),
            nn.ReLU(),
            nn.Linear(2, 1)
        )

    def forward(self, x):
        y_pred = self.network(x)
        return y_pred

网络结构：self.network是一个由多个层组成的序列，使用nn.Sequential来组织。这意味着数据将按照定义的顺序依次通过这些层。

• 第一层：nn.Linear(10, 5)，这是一个全连接层，将输入特征从10维减少到5维。
• 第二层：nn.Sigmoid()，这是一个激活函数，将第一层的输出通过Sigmoid函数，输出值范围在0到1之间，通常用于二分类问题。
• 第三层：nn.Linear(5, 2)，又一个全连接层，将特征从5维减少到2维。
• 第四层：nn.Sigmoid()，再次使用Sigmoid激活函数。
• 第五层：nn.Linear(2, 1)，将特征从2维减少到1维，这通常意味着模型的输出是一个单一的值。
• 第六层：nn.Sigmoid()，最后一层也是Sigmoid激活函数。

前向传播：forward方法定义了数据通过模型的方式。输入x将通过self.network，即上面定义的序列，最终得到预测值y_pred。
输出：模型的输出是一个经过Sigmoid函数的单一值。这意味着无论输入特征如何，模型的输出都将是一个介于0和1之间的值，这通常用于二元分类问题，其中输出可以解释为属于某个类别的概率。
模型训练有六个步骤：数据集加载、模型定义、损失函数定义、优化器定义、训练模型、测试模型。一般情况下数据加载时会得到两部分数据：训练集与测试集，训练集通常用于模型训练或作为测试集的一部分，测试集用于测试所得到模型的准确度也可提高模型的泛化能力。
下面是模型训练的代码，此次训练直接使用所有测试集，且并未添加测试集。

def train():
    # step1 数据加载
    x_data, y_data = dataLoader()
    # step2 模型定义
    model = my_model()

    # step3 损失函数定义
    loss = nn.MSELoss()
    # step4 优化器定义
    optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
    # step5 训练
    loss_list = []
    for i in range(5):
        _loss_list = []
        for epoch in range(100):
            # 前向传播
            y_pred = model(x_data)
            # 计算损失
            loss_value = loss(y_pred, y_data)
            _loss_list.append(loss_value.item())
            # 反向传播
            optimizer.zero_grad()
            loss_value.backward()
            # 更新参数
            optimizer.step()
        loss_list.append(_loss_list)
    # 绘制损失曲线
    draw_liners((range(len(loss_list[0])), loss_list[0], '-', 'liner1'),
                (range(len(loss_list[1])), loss_list[1], '--', 'liner2'),
                (range(len(loss_list[2])), loss_list[2], '-.', 'liner3'),
                (range(len(loss_list[3])), loss_list[3], ':', 'liner4'),
                (range(len(loss_list[4])), loss_list[4], 'solid', 'liner5'),
                labels=['epoch', 'loss vale'], img_name="loss liners0",
                is_display=False, is_save=True, imgs_path=IMAGES_PATH)

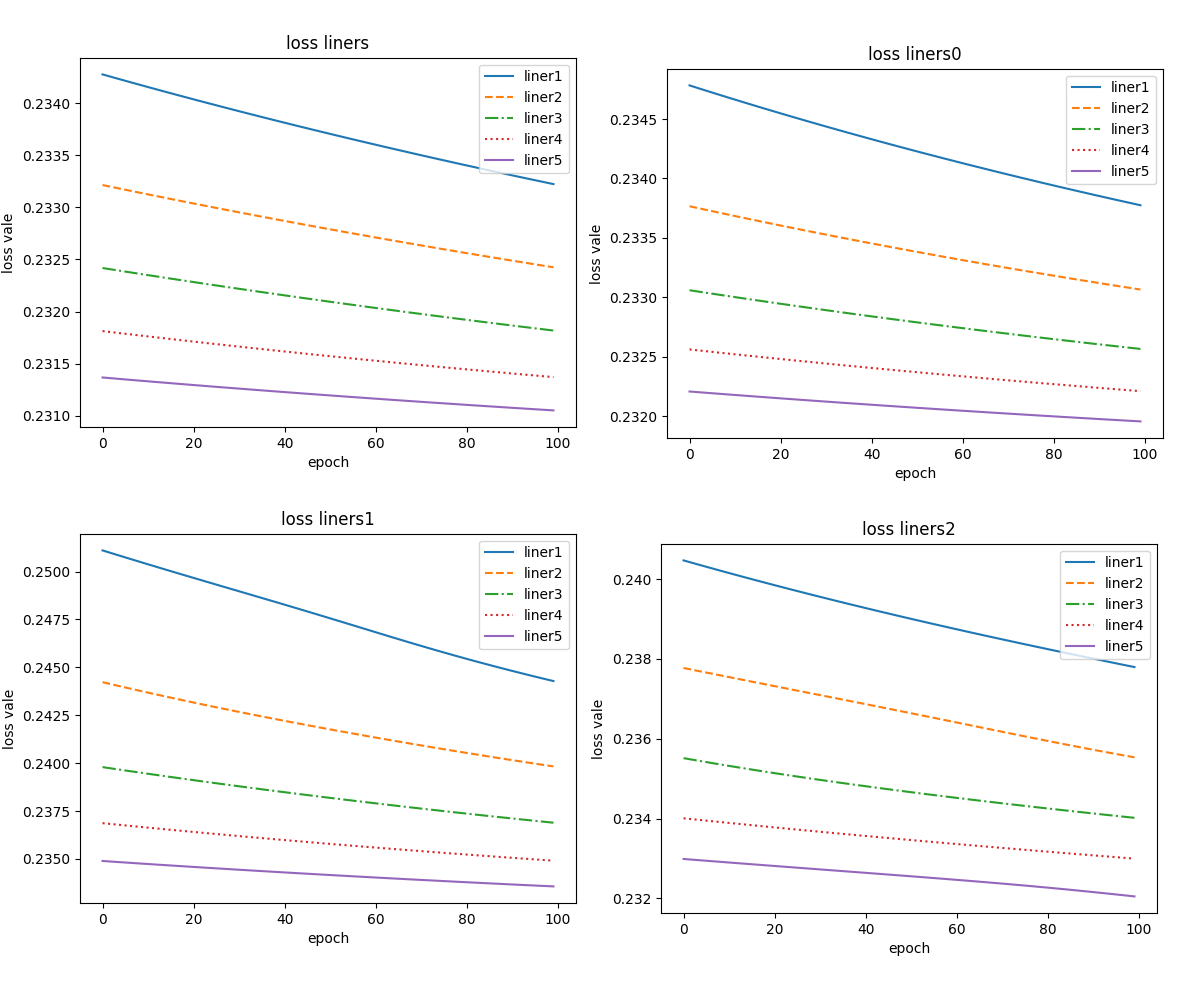
未添加随机数种子时，得到结果：

添加随机数种子后得到结果

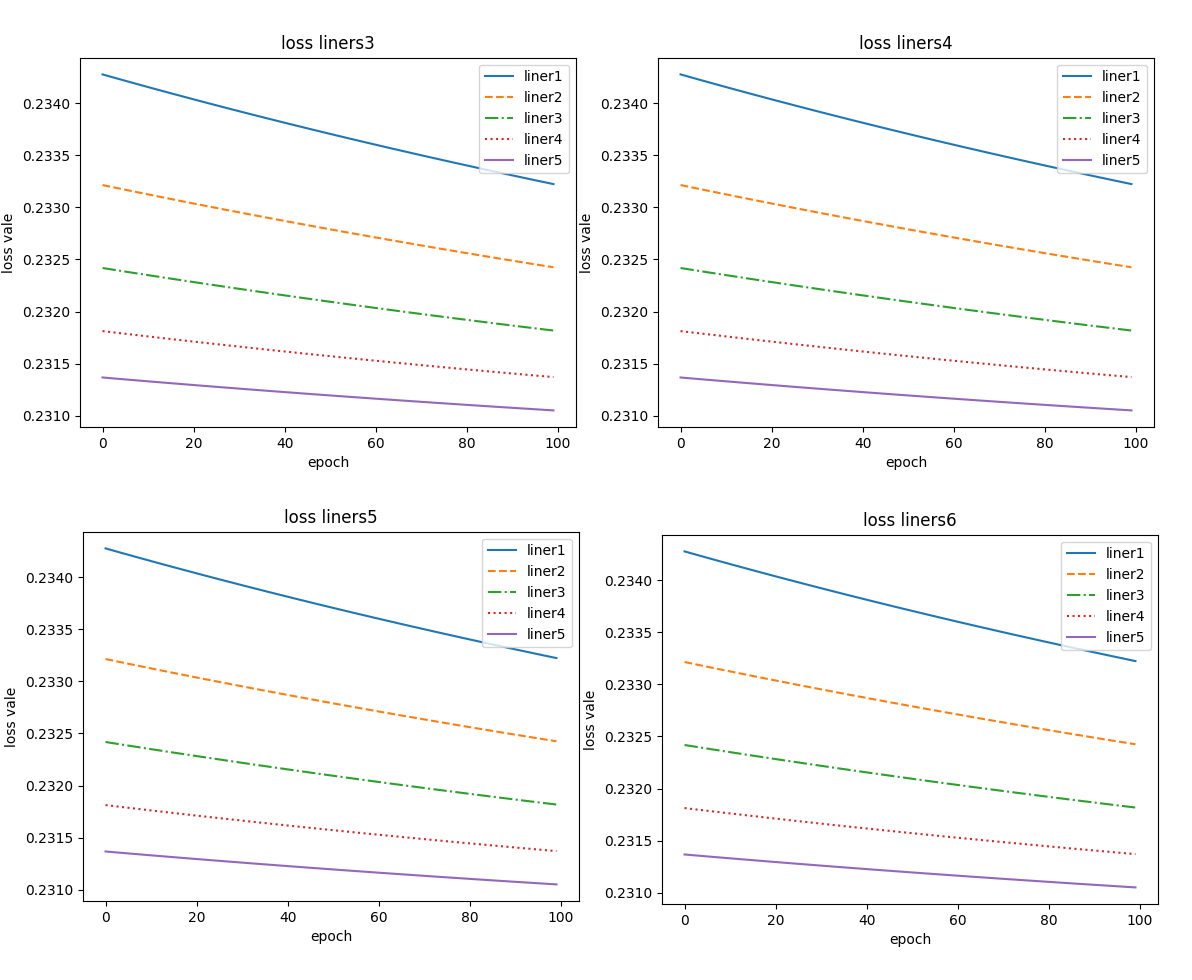
在 pytorch 中可使用torch.manual_seed(11) 添加随机数种子，添加随机数种子用于初始化随机数生成器的状态，能够确保实验的可重复性。

问题阐述与分析

好！那么问题来了。

• 上述八张图片中曲线的线型大致一致，均为单调减函数，同一个 liner 相差并不是特别大，但不同 liner 数值上相差非常大。
• 未添加随机数种子时，每次训练所得到的曲线虽然线型一致，但是值存在一定的误差。
• 而添加随机数种子后，每次重新训练每个单独的 liner 都一样，但是不同 liner 值却不一样。

询问 AI 后，看 AI 的结果：

使用相同模型和数据集进行训练时，每次运行得到的损失值可能会不同，这可能是由以下几个因素导致的：

1. 初始化权重的差异：神经网络在训练前需要初始化权重，不同的初始化方法或随机种子会导致权重初始化值不同，从而影响最终的损失值 。
2. 学习率设置：如果学习率过大，可能会导致损失值突然变得很大，即模型训练出现“跑飞”的情况 。
3. 数据集的划分和顺序：即使是相同的数据集，不同的数据划分和读取顺序也可能导致每次训练损失值波动 。
4. 优化器的选择和配置：不同的优化器（如SGD、Adam等）或其配置参数（如动量、衰减率等）会影响模型训练的动态过程，进而影响损失值 。
5. 正则化策略：正则化项的加入和参数（如L1、L2正则化的系数）会影响损失函数的值，不同的正则化设置可能导致损失值的变化 。
6. 梯度消失或爆炸问题：在深度学习中，梯度消失或爆炸问题可能导致模型训练不稳定，从而影响损失值的稳定下降 。
7. 训练过程中的随机性：如Dropout等引入随机性的操作，每次执行时都可能不同，进而影响损失值 。
8. 数据预处理：数据的标准化、归一化等预处理步骤的不同，也可能导致损失值的波动 。
9. 模型结构设计：模型结构的不同，如层数、神经元数量等，也会影响损失值的最终结果 。
10. 损失函数的选择：不同的损失函数可能对模型训练过程中的损失值有不同的影响，特别是在分类问题中，交叉熵损失函数的选择会对损失值产生影响 。

---

小编的想法：

• 计算精度：因为计算机内部参与运算的数据大小会受到一定的限制，这就有可能会造成最终结果产生一定误差。在控制台中打印每次 loss 得到结果loss_value.item()=0.2310512214899063，个人猜测这种可能性较小。
• 模型的随机性：神经网络算法具有一定的随机性，如初始化随机权重，因此用同样的数据训练同一个网络会得到不同的结果。模型定义时，可使用下面这段代码查看模型参数。

self.linear = nn.Linear(in_features, out_features)
for name, p in self.linear.named_parameter():
    print(name, ": ", p)

• 第三方库的随机性：在本模型中，并未引入任何第三方库，因此小编认为此种情况不符合这个实例。

【Python 】数据可视化入门：使用 Matplotlib、Numpy 和 SciPy 绘制精美曲线曲面图