更多精彩,关注博客园主页,不断学习!不断进步!
我的主页
csdn很少看私信,有事请b站私信
博客园主页-发文字笔记-常用
有限元鹰的主页 内容:
- ABAQUS数值模拟相关
- Python科学计算
- 开源框架,编程学习笔记
哔哩哔哩主页-发视频-常用
FE-有限元鹰的个人空间 内容:
- 模拟案例
- 网格划分
- 游戏视频,及其他搬运视频
文章目录
- 我的主页
- 博客园主页-发文字笔记-常用
- 哔哩哔哩主页-发视频-常用
- 线性方程组迭代算法的Python实现
- jacobi,GS,SOR迭代法
- 正定对称线性方程组的不定常迭代:最速下降法,共轭梯度法
线性方程组迭代算法的Python实现
jacobi,GS,SOR迭代法
def JacobiIter(A:np.ndarray,
b:np.ndarray,
tol:float=1e-5,
maxIter:int=100)->Tuple[np.ndarray,np.ndarray]:
"""使用Jacobi迭代法求解线性方程组Ax=b
input:
A: np.ndarray, 系数矩阵
b: np.ndarray, 右端常数
tol: float, 误差限
maxIter: int, 最大迭代次数
output:
x: np.ndarray, 解向量
errors: np.ndarray, 误差序列
"""
from numpy import dot
from numpy.linalg import norm
x0=np.zeros(b.shape)
L=-1*np.tril(A,k=-1).copy()
U=-1*np.triu(A,k=1).copy()
D=np.diag(np.diag(A)).copy()
Dinv=np.linalg.inv(D)
errors=[]
for i in range(maxIter):
x_next=dot(Dinv,(dot((L+U),x0)+b))
# error check
error=norm(b-dot(A,x_next),2)/norm(b,2)
errors.append(error)
if error<tol:
return x_next,np.array(errors)
else:
x0=x_next
def GaussIter(A:np.ndarray,
b:np.ndarray,
tol:float=1e-5,
maxIter:int=100)->Tuple[np.ndarray,np.ndarray]:
"""使用Gauss-Seidel迭代法求解线性方程组Ax=b
input:
A: np.ndarray, 系数矩阵
b: np.ndarray, 右端常数
tol: float, 误差限
maxIter: int, 最大迭代次数
output:
x: np.ndarray, 解向量
errors: np.ndarray, 误差序列
"""
from numpy import dot
from numpy.linalg import norm
x0=np.zeros(b.shape)
L=-1*np.tril(A,k=-1).copy()
U=-1*np.triu(A,k=1).copy()
D=np.diag(np.diag(A)).copy()
DsubLinv=np.linalg.inv(D-L)
errors=[]
for i in range(maxIter):
x_next=DsubLinv.dot(U).dot(x0)+DsubLinv.dot(b)
# error check
error=norm(b-dot(A,x_next),2)/norm(b,2)
errors.append(error)
if error<tol:
return x_next,np.array(errors)
else:
x0=x_next
def SORIter(A:np.ndarray,
b:np.ndarray,
w:float=1.0,
tol:float=1e-5,
maxIter:int=100)->Tuple[np.ndarray,np.ndarray]:
"""使用SOR迭代法求解线性方程组Ax=b
input:
A: np.ndarray, 系数矩阵
b: np.ndarray, 右端常数
w: float, 松弛因子(0~2.0)
tol: float, 误差限
maxIter: int, 最大迭代次数
output:
x: np.ndarray, 解向量
errors: np.ndarray, 误差序列
"""
from numpy import dot
from numpy.linalg import norm
x0=np.zeros(b.shape)
L=-1*np.tril(A,k=-1).copy()
U=-1*np.triu(A,k=1).copy()
D=np.diag(np.diag(A)).copy()
DsubOmegaLinv=np.linalg.inv(D-w*L)
errors=[]
for i in range(maxIter):
x_next=DsubOmegaLinv.dot((1-w)*D+w*U).dot(x0)+w*DsubOmegaLinv.dot(b)
# error check
error=norm(b-dot(A,x_next),2)/norm(b,2)
errors.append(error)
if error<tol:
return x_next,np.array(errors)
else:
x0=x_next
- 验证
import numpy as np
from formu_lib import *
A=np.array([[2,-1,0],
[-1,3,-1],
[0,-1,2]])
b=np.array([1,8,-5])
extractVal=np.array([2,3,-1])
x1,er1=JacobiIter(A,b)
x2,er2=GaussIter(A,b)
x3,er3=SORIter(A,b,1.2)
ind1,ind2,ind3=list(range(len(er1))),list(range(len(er2))),list(range(len(er3)))
plotLines([ind1,ind2,ind3],[er1,er2,er3],["Jacobi iter error","Gauss iter error","SOR iter error"])
showError(x1,extractVal)
showError(x2,extractVal)
showError(x3,extractVal)
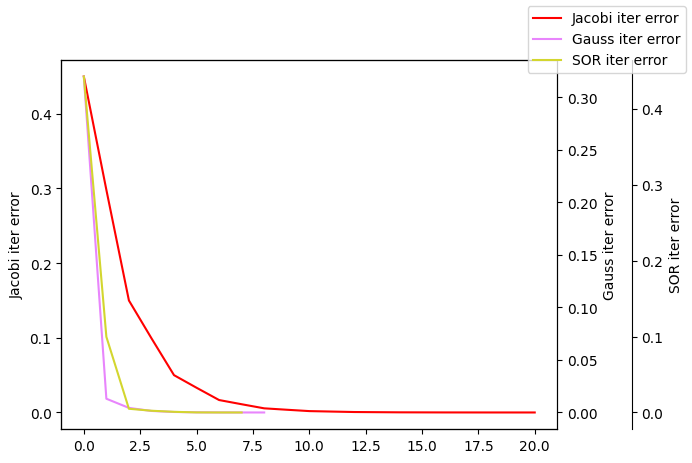
# 雅可比迭代法
数值解: [ 1.9999746 2.99999435 -1.0000254 ],
精确解: [ 2 3 -1],
误差: 9.719103983280175e-06
# GS迭代法
数值解: [ 1.9999619 2.9999746 -1.0000127],
精确解: [ 2 3 -1],
误差: 1.2701315856479742e-05
# SOR迭代法
数值解: [ 2.00001461 2.999993 -1.00000098],
精确解: [ 2 3 -1],
误差: 4.338862621105977e-06
正定对称线性方程组的不定常迭代:最速下降法,共轭梯度法
def SPDmethodSolve(A:np.ndarray,
b:np.ndarray,
tol:float=1e-5,
maxIter:int=200)->Tuple[np.ndarray,np.ndarray]:
"""使用最速下降法求解线性方程组Ax=b
input:
A: np.ndarray, 系数矩阵,必须是对称正定矩阵
b: np.ndarray, 右端常数
tol: float, 误差限
maxIter: int, 最大迭代次数
output:
x: np.ndarray, 解向量
errors: np.ndarray, 误差序列
"""
from numpy import dot
from numpy.linalg import norm
x0=np.zeros(b.shape)
i,errors=0,[]
while True :
if i>maxIter:
maxIter=1.5*maxIter
print(f"迭代次数过多,自动调整为 {maxIter}")
# 计算残量r^k作为前进方向.
r=b-dot(A,x0)
# 计算前进距离a_k
a=InnerProduct(r,r)/InnerProduct(dot(A,r),r)
x_next=x0+a*r
error=norm(b-dot(A,x_next),2)/norm(b,2)
errors.append(error)
if errors[-1]<tol:
return x_next,np.array(errors)
else:
x0=x_next
i+=1
def conjGrad(A:np.ndarray,
b:np.ndarray,
tol:float=1e-5,
maxIter:int=200)->Tuple[np.ndarray,np.ndarray]:
"""使用共轭梯度法求解线性方程组Ax=b
input:
A: np.ndarray, 系数矩阵,必须是对称正定矩阵
b: np.ndarray, 右端常数
tol: float, 误差限
maxIter: int, 最大迭代次数
output:
x: np.ndarray, 解向量
errors: np.ndarray, 误差序列
"""
from numpy import dot
from numpy.linalg import norm
# 选择初值x0,初始方向p0=r0=b-Ax0
x0=np.zeros(b.shape)
i,errors=0,[]
r0=b-dot(A,x0)
p_0=b-dot(A,x0)
errors.append(norm(r0,2)/norm(b,2))
while True :
if i>maxIter:
maxIter=1.5*maxIter
print(f"迭代次数过多,自动调整为 {maxIter}")
# 计算a_k,x^{k+1}=x_k+a_k*p_k
a_k=InnerProduct(r0,p_0)/InnerProduct(dot(A,p_0),p_0)
x_next=x0+a_k*p_0
# 计算下一步的残量
r_k_next=b-dot(A,x_next)
errors.append(norm(r_k_next,ord=2)/norm(b,2))
# 如果残量足够小,则停止迭代
if errors[-1]<tol:
return x_next,np.array(errors)
else:
# 计算下一步的搜索方向
beta_k=-1*InnerProduct(r_k_next,A.dot(p_0))/InnerProduct(p_0,A.dot(p_0))
p_0=r_k_next+beta_k*p_0
x0=x_next
i+=1
- 验证

from formu_lib import *
import numpy as np
A=np.array([[4,-1,0],
[-1,4,-1],
[0,-1,4]])
b=np.array([3,2,3])
extractVal=np.array([1,1,1])
x1,er1=SPDmethodSolve(A,b,1e-6)
x2,er2=conjGrad(A,b,1e-6)
plotLines([list(range(len(er1))),list(range(len(er2)))],[er1,er2],["SPD method error","conjugate gradient error"])
showError(x1,extractVal)
showError(x2,extractVal)
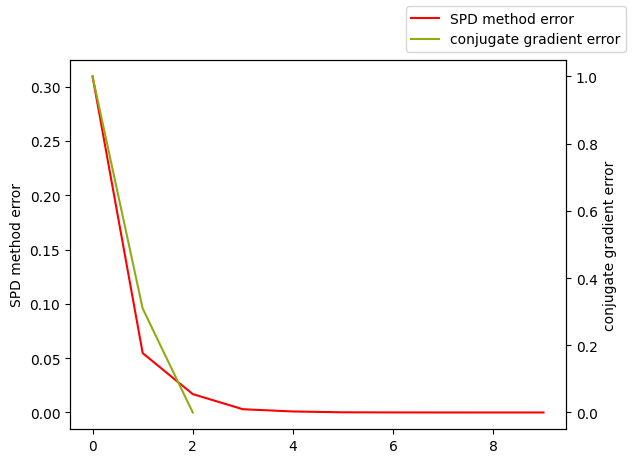
# SPD method
数值解: [0.99999951 0.99999951 0.99999951],
精确解: [1 1 1],
误差: 4.891480784863234e-07
# conjugate gradient method
数值解: [1. 1. 1.],
精确解: [1 1 1],
误差: 0.0