因子分析 (Factor Analysis, FA)

因子分析是一种统计方法，用于通过少量潜在变量（因子）解释观测数据中的相关结构。它在数据降维、特征提取和变量选择中广泛应用。

原理

因子分析假设观测变量是由少数潜在因子线性组合并加上噪声得到的。通过估计因子载荷矩阵和因子方差，可以解释数据的相关结构。

公式推理

1. 线性模型： 给定观测数据矩阵 X 和因子矩阵 F，模型可以表示为：

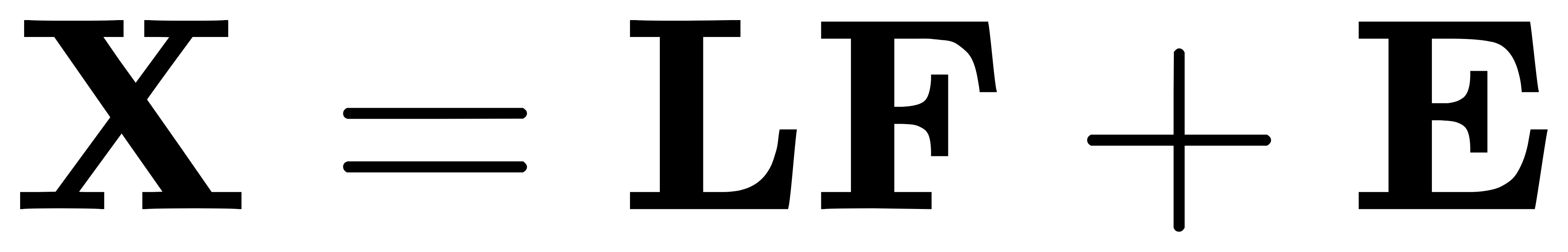
其中，L 是因子载荷矩阵，E 是噪声矩阵。

1. 因子协方差： 假设因子 F 的协方差矩阵为 Ψ，噪声 E 的协方差矩阵为 Θ，则观测数据 X 的协方差矩阵为：

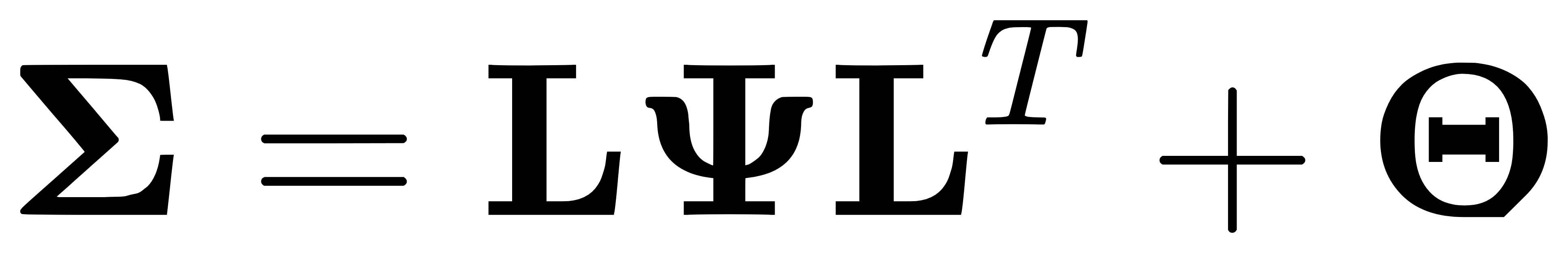
1. 估计参数： 通过最大似然估计（MLE）或主成分方法，可以估计因子载荷矩阵 L 和因子方差矩阵 Ψ。

经典案例

案例：FA在心理学问卷数据中的应用

我们将使用一个假设的心理学问卷数据集，其中包含若干个问题的回答。通过因子分析，可以识别出潜在的心理因素。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FactorAnalysis
from sklearn.preprocessing import StandardScaler

# 生成假设的心理学问卷数据
np.random.seed(0)
n_samples = 1000
n_features = 10

# 假设数据是由三个潜在因子生成的
true_factors = np.random.normal(size=(n_samples, 3))
loading_matrix = np.random.normal(size=(3, n_features))
X = np.dot(true_factors, loading_matrix) + np.random.normal(size=(n_samples, n_features))

# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 使用因子分析进行降维
fa = FactorAnalysis(n_components=3, random_state=42)
X_fa = fa.fit_transform(X_scaled)

# 可视化因子载荷
plt.figure(figsize=(12, 6))
plt.imshow(fa.components_, cmap='viridis', aspect='auto')
plt.colorbar(label='Loading Value')
plt.title('Factor Loadings')
plt.xlabel('Feature')
plt.ylabel('Factor')
plt.show()

代码解析

1. 生成假设的心理学问卷数据：假设数据由三个潜在因子生成，使用随机数生成因子和载荷矩阵。
2. 标准化数据：使用 StandardScaler 对数据进行标准化处理，使得每个特征具有零均值和单位方差。
3. 使用因子分析进行降维：创建因子分析对象并将数据降到三个因子。
4. 可视化因子载荷：绘制因子载荷矩阵，展示每个因子与原始特征之间的关系。

代码展示了如何利用因子分析对高维数据进行降维，并通过可视化直观地展示了因子与原始特征的关系，有助于理解因子分析在数据特征提取中的应用。

非负矩阵分解 (Non-negative Matrix Factorization, NMF)

NMF 是一种矩阵分解方法，它将一个非负矩阵分解成两个非负矩阵的乘积，广泛用于数据降维、主题建模和推荐系统。

原理

NMF 通过将原始数据矩阵 X 分解为两个非负矩阵 W 和 H 的乘积来近似原始数据。矩阵 W 和 H 分别表示低维特征和基向量。

公式推理

1. 非负矩阵分解： 给定一个 m×n 非负矩阵 X，NMF 将其分解为 m×k 非负矩阵 W 和 k×n 非负矩阵 H，使得：

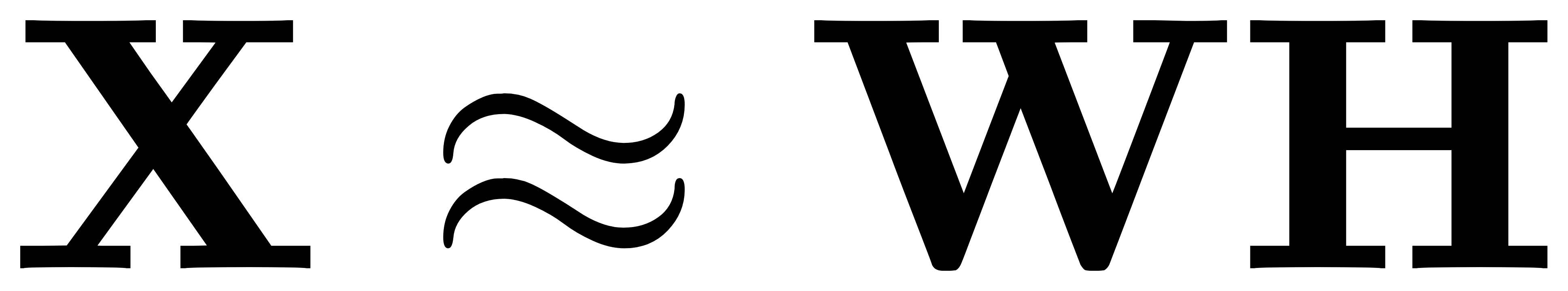
1. 优化目标： 最小化原始矩阵和分解矩阵的 Frobenius 范数：

其中，∥⋅∥F 表示 Frobenius 范数。

1. 约束条件：

经典案例

案例：NMF 在图像数据集上的应用

我们将使用 Olivetti 面部图像数据集，该数据集包含 400 张面部图像，每张图像是 64x64 像素的灰度图像。通过 NMF 将面部图像数据降维，并可视化基向量。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn.decomposition import NMF
from sklearn.preprocessing import MinMaxScaler

# 加载 Olivetti 面部图像数据集
faces = fetch_olivetti_faces(shuffle=True, random_state=42)
X = faces.data

# 使用 MinMaxScaler 进行数据归一化
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

# 使用 NMF 进行降维
n_components = 10
nmf = NMF(n_components=n_components, random_state=42)
W = nmf.fit_transform(X_scaled)
H = nmf.components_

# 可视化基向量
fig, axes = plt.subplots(2, 5, figsize=(15, 6),
                         subplot_kw={'xticks':(), 'yticks':()})
for i, ax in enumerate(axes.flat):
    ax.imshow(H[i].reshape(64, 64), cmap='gray')
    ax.set_title(f'Component {i+1}')
plt.suptitle('NMF Components')
plt.show()

代码解析

1. 加载 Olivetti 面部图像数据集：使用 fetch_olivetti_faces 函数加载面部图像数据集，包括特征矩阵 X。
2. 标准化数据：使用 StandardScaler 对数据进行标准化处理，使得每个特征具有零均值和单位方差。
3. 使用 NMF 进行降维：创建 NMF 对象并将数据降到 10 个组件。
4. 可视化基向量：绘制 NMF 基向量，每个基向量表示一个特征模式。

实战应用：

1. 数据加载与预处理

真实照片可能需要从文件系统中读取，并进行一些预处理操作。这包括读取图像文件、调整图像尺寸和进行归一化。

2. 代码修改步骤

1. 读取图像：你可以使用像 PIL 或 OpenCV 这样的库来读取和处理图像。
2. 调整图像尺寸：确保所有图像尺寸一致，以便可以将它们转化为相同的特征维度。
3. 数据归一化：确保图像数据在 [0, 1] 范围内。

以下是一个示例代码，演示如何处理真实照片并使用 NMF：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import NMF
from sklearn.preprocessing import MinMaxScaler
from PIL import Image
import os

# 设置图像文件路径和参数
image_dir = 'path_to_your_images_directory'  # 替换为图像文件夹的路径
image_size = (64, 64)  # 目标图像尺寸

# 读取图像并转换为数组
def load_images_from_folder(folder, size):
    images = []
    for filename in os.listdir(folder):
        img_path = os.path.join(folder, filename)
        with Image.open(img_path) as img:
            img = img.convert('L')  # 转为灰度图像
            img = img.resize(size)  # 调整图像尺寸
            img_array = np.array(img).flatten()  # 展平图像
            images.append(img_array)
    return np.array(images)

# 加载图像数据
X = load_images_from_folder(image_dir, image_size)

# 数据归一化
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

# 使用 NMF 进行降维
n_components = 10  # 选择适当的组件数量
nmf = NMF(n_components=n_components, random_state=42)
W = nmf.fit_transform(X_scaled)
H = nmf.components_

# 可视化 NMF 基向量
fig, axes = plt.subplots(2, 5, figsize=(15, 6), subplot_kw={'xticks':(), 'yticks':()})
for i, ax in enumerate(axes.flat):
    ax.imshow(H[i].reshape(image_size), cmap='gray')
    ax.set_title(f'Component {i+1}')
plt.suptitle('NMF Components')
plt.show()

说明

1. 读取图像：

• • 使用 PIL 库的 Image.open() 函数读取图像。
  • 将图像转换为灰度图像（如果不需要颜色通道），并调整到指定的尺寸。

1. 归一化：

• • 使用 MinMaxScaler 将图像数据归一化到 [0, 1] 范围。

1. NMF 降维：

• • 设置 n_components 为你希望的特征数量。
  • 使用 NMF 进行降维，并可视化基向量。

1. 图像尺寸：

• • 确保所有图像的尺寸一致，以便将它们展平为固定长度的特征向量。

额外的考虑

• 图像质量：处理真实照片时，图像质量和分辨率会影响结果。确保图像清晰并适合分析。
• 数据集大小：对于大量图像，可能需要考虑数据的加载和处理效率。

代码展示了如何利用 NMF 对高维数据进行降维，并通过可视化直观地展示了基向量，有助于理解 NMF 在数据特征提取中的应用。