直观理解

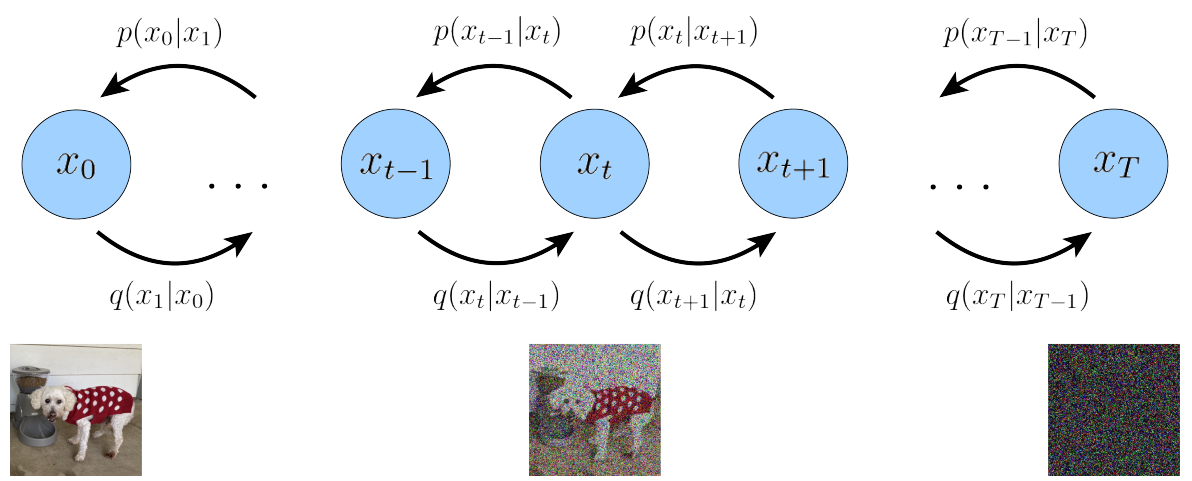
扩散模型分为前向过程（扩散过程，Data$\to$Noise）和后向过程（生成过程或逆扩散过程，Noise$\to$Data）。在前向过程中，对于每一个观测样本，不断向样本中添加少量噪声，直到该样本完全被摧毁成为完全随机的噪声，该噪声属于正态分布；从正态分布中随机采样一个噪声样本，不断的对该样本去除少量的噪声，直到该噪声样本成为像真实样本的生成样本。前向过程的噪声是事先设置好的，该噪声还被用于神经网络训练，然后使用神经网络生成后向过程的噪声。

生成模型

给定从一个感兴趣的分布中观察到的样本$x$(比如图像数据集)，生成模型的目标是学习建模其真实的数据分布$p(x)$。一旦学习到，我们就可以从我们的近似模型中生成新的样本。
我们可以认为我们观察到的数据$x$是由相关的未见的潜在变量表示或生成的，我们可以用随机变量$z$来表示这种潜在变量。表达这一思想的最佳直觉来源于柏拉图的《洞穴寓言》。在这个寓言中，一群人终生被锁链困在洞穴中，他们只能看到面前墙上投射的二维影子，而这些影子是由经过火前的未见的三维物体生成的。对于这些人来说，他们所观察到的一切实际上都是由他们永远无法看到的高维抽象概念决定的。
类似地，我们在现实世界中遇到的物体也可能是一些更高层次表征的函数生成的；例如，这些表征可能包含抽象属性，如颜色、大小、形状等。然后，我们所观察到的可以被解释为这些抽象概念的三维投影或实例化，就像洞穴中的人们观察到的实际上是三维物体的二维投影一样。虽然洞穴中的人们永远无法看到（甚至完全理解）隐藏的物体，但他们仍然可以推理并得出关于这些物体的结论；同样地，我们也可以近似描述我们所观察到的数据的潜在表征。
尽管柏拉图的洞穴寓言阐明了潜在变量作为决定观测结果的潜在不可观察表征的概念，但这个类比的一个警告是，在生成建模中，我们通常寻求学习低维潜在表征，而不是高维表征。这是因为在没有强先验知识的情况下，尝试学习比观测值更高维度的表征是一项徒劳的努力。另一方面，学习低维潜在表征也可以视为一种压缩形式，并且有可能揭示描述观测结果的语义上有意义的结构。
在数学上，我们可以想象潜在的变量和我们观察到的数据是由一个联合分布$p(x,z)$建模的。这个过程可以强调数据生成过程$p(x,z)=p(z)p(x|z)$。即从潜在变量分布中$p(z)$采样潜在变量$z$，$p(z)$是一个数学上明确定义的随机变量，比如高斯分布、均匀分布等；对于潜在变量$z$，根据条件分布$p(x|z)$生成观测样本，在变分自编码器中，条件分布$p(x\mid z)$通常由一个神经网络（解码器）进行参数化，在生成对抗模型中，条件分布$p(x\mid z)$由生成器 $G(z)$ 定义。
目前生成模型可以根据他们概率分布的方式分为两类，显式生成模型和隐式生成模型。

显式生成模型

通过（近似）最大似然直接学习分布的概率密度（或质量）函数（即学习一个为观察到的数据样本分配高可能性的模型），所以显式生成模型又被称为基于似然的模型。典型的显式生成模型包括自回归模型、标准化流模型、能量基模型、高斯混合模型、自回归模型、变分自编码器、隐马尔可夫模型等 ，本文的扩散模型也属于这一类。

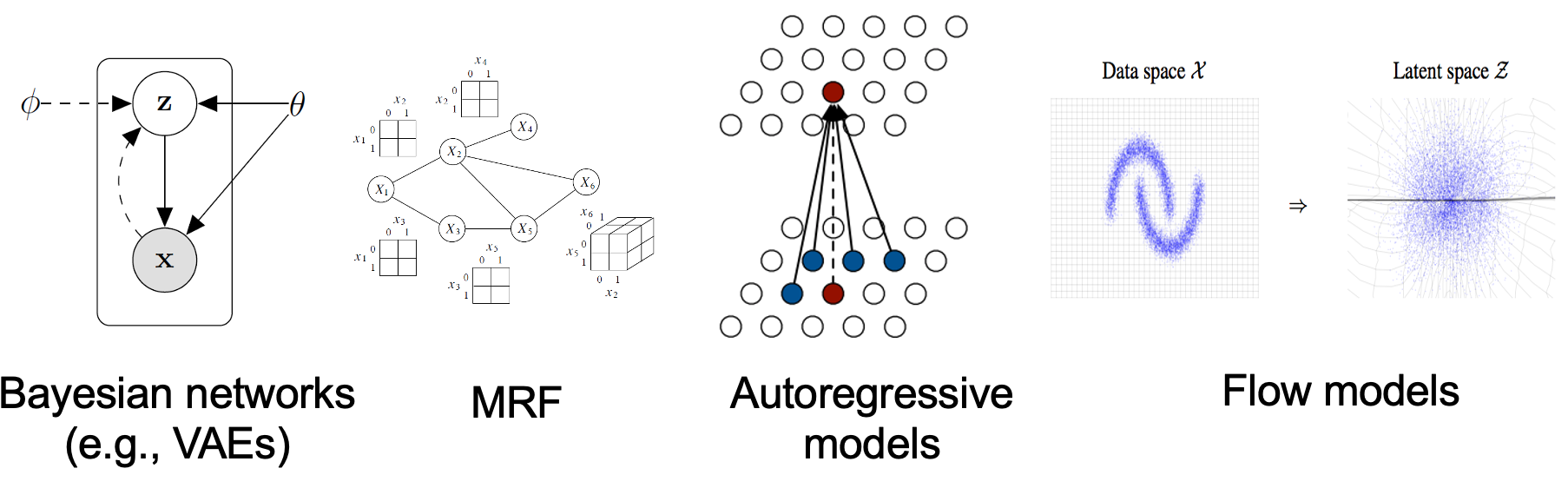
隐式生成模型

概率分布由其采样过程的模型隐式表示。最突出的例子是生成对抗网络（GAN），通过使用神经网络变换随机高斯向量来合成来自数据分布的新样本。

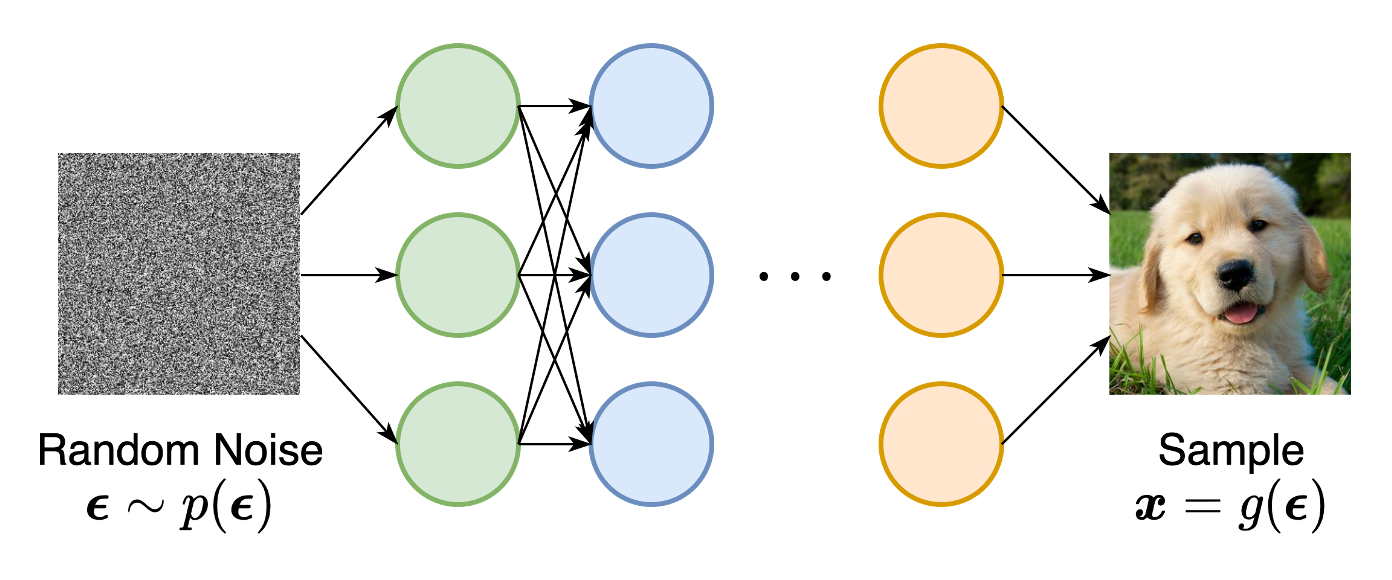
数学理解

首先明确一点：$x_0$是可观测的干净数据，我们有其样本（比如我们数据集中的图片、音频等），但是我们不知道其真实分布$p(x_0)$。$x_T$是纯噪声数据，其先验分布为标准正态分布$\mathcal{N}(x_T;0,\mathrm{I})$。$x_1,x_2,...,x_{T-1}$为带噪声的数据。$x_1,x_2,...,x_T$都是潜在变量。如图2所示。注意$p(x_{t-1}|x_t)$和$p_{\theta }(x_{t-1}|x_t)$相同。

扩散过程

扩散模型在正向扩散过程中，通过逐渐向数据样本中加入噪声，使其最终转化为近似标准正态分布的样本。这个过程通常被描述为一个马尔可夫链。对于扩散过程我们可扩散模型在正向扩散过程中，通过逐渐向数据样本中加入噪声，使其最终转化为近似标准正态分布的样本。这个过程通常被描述为一个马尔可夫链以表示为联合分布$q(x_{1:T}|x_0)$，如公式（1）所示，表示了给定观测数据$x_0$，生成潜在变量$x_1,x_2,...,x_T$的过程。其中潜在变量$x_t\sim q(x_t|x_{t-1})$如公式（2）所示，也被称为转移核，${\beta }_1,{\beta }_2,...,{\beta }_T$是噪声方差表，是人工设置的固定值。所以知道了噪声数据$x_{t-1}$和方差表，公式2的分布就是已知的，所以就能通过采样得到噪声数据$x_t$。这里$x_t$的获取过程与我们直观理解“向样本中加入噪声”似乎不太一样。但是根据重采样技巧，我们可以继续将公式（2）写作$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{ϵ}_t$，其中${ϵ}_t\sim \mathcal{N}(0,\mathrm{I})$。这样就可以很好的理解加噪步骤，首先从标准正态分布中采样随机噪声${ϵ}_t$，然后对于样本$x_{t-1}$加入噪声样本$(\sqrt{1-{\beta }_t}-1)x_{t-1}+\sqrt{{\beta }_t}{ϵ}_t$得到样本$x_t$。这与我们直观理解的加噪过程是符合的，然而这仍然不是最终代码实现的方式。可以进一步将 $x_t$ 表示为初始数据样本 $x_0$ 和一系列独立同分布的高斯噪声之和的形式。具体如公式（3）或（4）。其中：${\alpha }_t=1-{\beta }_t$、${\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$是累积乘积、$ϵ\sim \mathcal{N}(0,I)$是服从标准正态分布的高斯噪声。这个公式表示了在第 $t$ 步直接从初始数据样本$x_0$ 生成$x_t$的过程。推导过程如下图所示。
$q(x_{1:T}|x_0)={\prod }_{i=1}^{T}q(x_t|x_{t-1})$ (1)
$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathrm{I})$ (2)
$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ$ (3)
$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)\mathrm{I})$ (4)

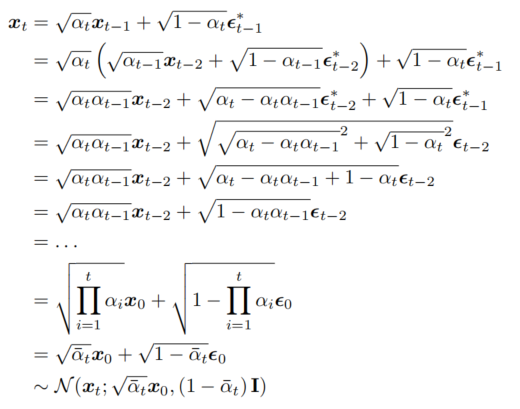
生成过程

对于生成过程我们可以表示为联合分布$p(x_{0:T})$。如公式（5）所示，$p(x_T)=\mathcal{N}(x_T;0,\mathrm{I})$,从标准正态分布不断生成$x_T,x_{T-1},...,x_t,..,x_2,x_1,x_0$的过程，首先从$p(x_T)$采样一个随机噪声$X_T$，然后生成的样本和中间样本如公式(6)所示，$\theta$表示神经网络的参数，$x_t$和$t$是神经网络的输入，$\mu$和$\Sigma$是模型的输出。但是我们并不知道$p(x_{t-1}|x_t)$，又应该如何训练神经网络呢？这可以通过目标函数的推导得到。
$p(x_{0:T})=p(x_T){\prod }_{t=1}^{T}p(x_t-1|x_t)$ (5)
$p(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t))$ (6)

目标函数

扩散模型也是通过（近似）最大似然直接学习分布的概率密度（或质量）函数，所以扩散模型是显式生成模型。
如图5所示，$\log p(x)$推导过程如下，可以分解为三个子项，所以最大化$\log p(x)$等价于对三个子项的处理。。第四行采用的詹森不等式变换，并且右侧式子就是ELBO（证据下界）。

1. reconstruction term：${\mathbb{E}}_{q(x_1|x_0)}[\log p_{\theta }(x_0|x_1)]\approx {\sum }_{i=1}^n\log p_{\theta }(x_0^i|x_1^i)$。右侧为采样的期望，n表示样本量。$p_{\theta }(x_0|x_1)$为预测最终的生成样本$x_0$，所以被称为重建项，需要最大化该项。
2. prior matching term：${\mathbb{E}}_{q(x_{T-1}|x_0)}[D_{KL}(q(x_T|x_{T-1})||p(x_T))]$是先验匹配项。当最终的潜在分布与高斯先验相匹配时，它被最小化。这个项不需要优化，因为它没有可训练的参数；此外，由于我们假设一个足够大的$T$，最终分布是高斯分布，这个项有效地变成零。
3. consistency term：${\mathbb{E}}_{q(x_{t-1},x_{t+1}|x_0)}[D_{KL}(q(x_t|x_{t-1})||p_{\theta }(x_t|x_{t+1}))]$是一致性项，需要最小化。它努力使得在$x_t$处的分布与前向和后向过程都一致。也就是说，从一个噪声较大的图像去噪步骤应该与一个噪声较小的图像的加噪步骤相匹配，对于每一个中间时间步都是如此；这在数学上通过KL散度反映出来。当我们训练 $p_{\theta }(x_t|x_{t+1})$ 以匹配高斯分布 $q(x_t|x_{t-1})$ 时，这一项被最小化,对应图5中绿色箭头和粉色箭头的最小化。可以通过蒙特卡罗估计和重参数化技巧后，再通过梯度下降进行优化，但是最终的代码也不是这样实现的。

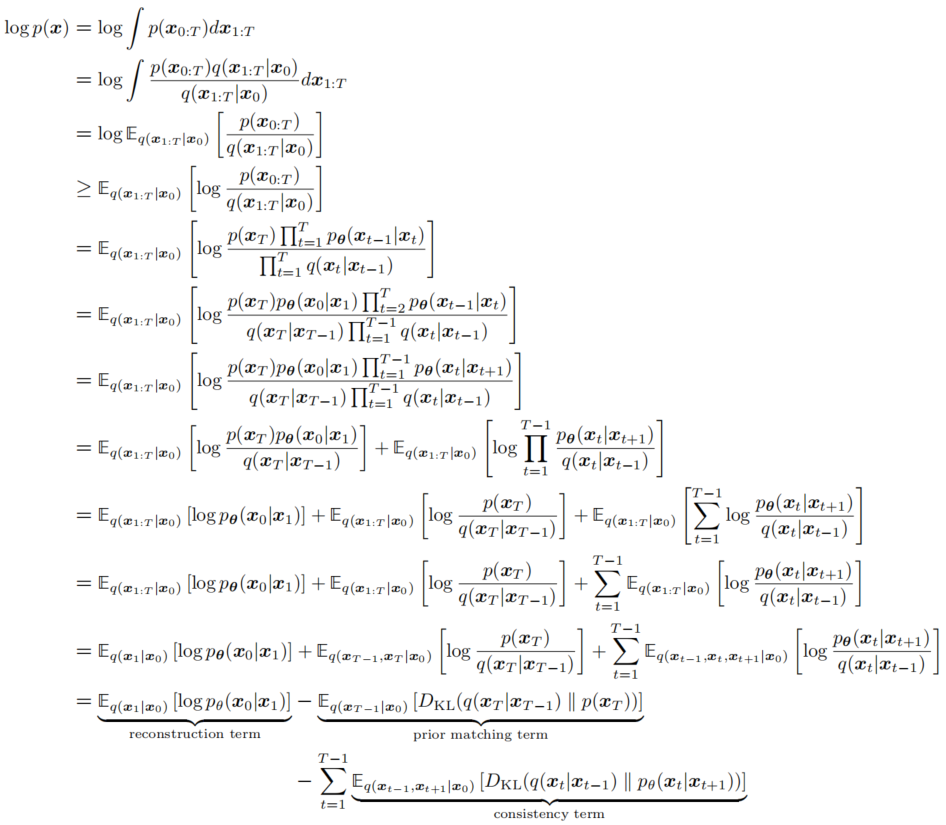
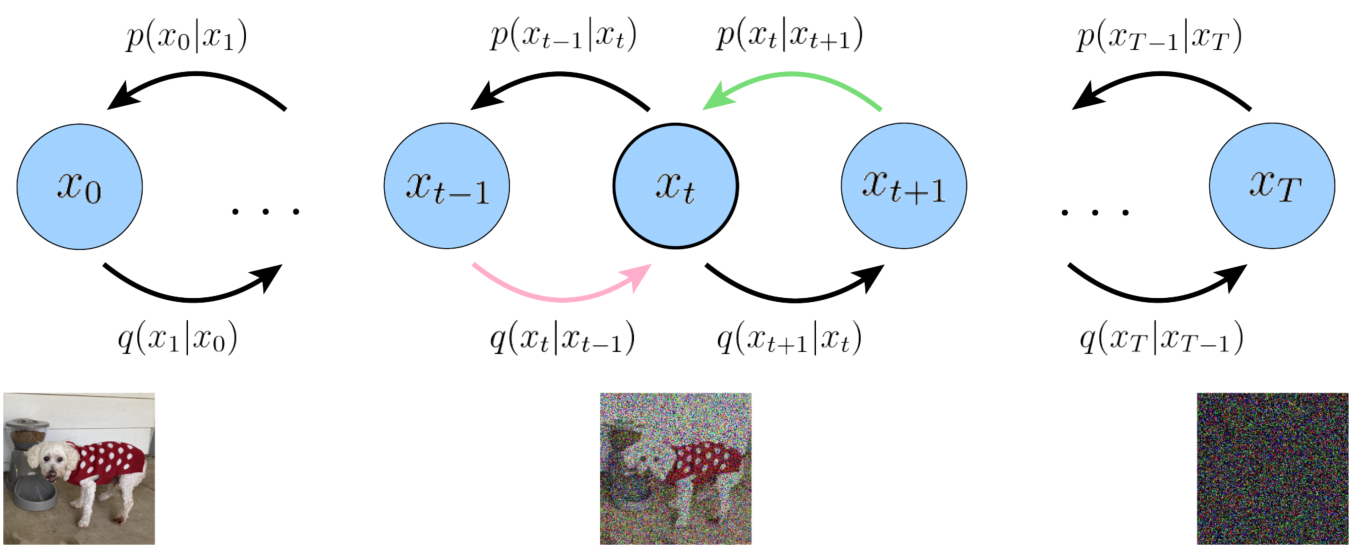
在这个推导下，ELBO（Evidence Lower Bound）的所有项都是作为期望值计算的，因此可以使用蒙特卡洛估计来近似。然而，实际上使用我们刚刚推导出的项来优化ELBO可能是次优的；因为一致性项是作为每个时间步两个随机变量$x_{t-1},x_{t+1}$的期望值计算的，其蒙特卡洛估计的方差可能比每个时间步只使用一个随机变量估计的项要高。由于它是通过求和$T-1$个一致性项计算的，对于较大的$T$值，ELBO的最终估计值可能会有高方差。
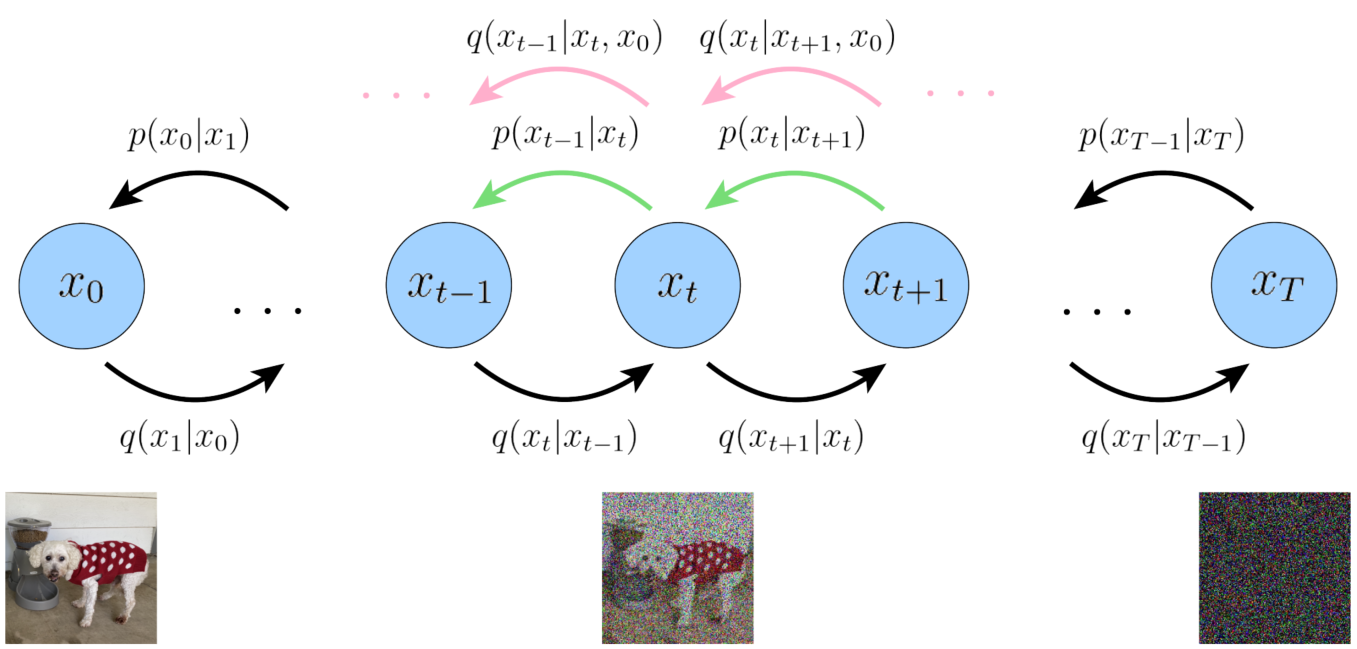
如图8所示，我们如果最小化绿色和粉色箭头，这样每个项都被计算一次只对一个随机变量的期望。首先我们进行一个变换，如公式（7）所示。
$q(x_t|x_{t-1},x_0)=\frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}$ (7)
如图7所示，$\log p(x)$另外一个推导过程如下，也可以分解为三个子项。

因此，我们成功地推导出一种可以用较低方差估计ELBO的解释，因为每一项最多是作为一个随机变量的期望值计算的。这种形式也有一个优雅的解释，当我们检查每个单独的项时，这种解释就会显现出来：重构项和先验匹配项和前面介绍的意义，虽然先验匹配项公式不相同。
对于去噪匹配项（denoising matching term），${\mathbb{E}}_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))]$。我们学习期望的去噪转移步骤 $p_{\theta }(x_{t-1}|x_t)$，作为可处理的真实去噪转移步骤 $q(x_{t-1}|x_t,x_0)$的近似。这个 $q(x_{t-1}|x_t,x_0)$ 转移步骤可以作为一个真实信号，因为它定义了在知道最终完全去噪的图像$x_0$的情况下，如何对一个噪声图像$x_t$进行去噪。因此，当两个去噪步骤的匹配尽可能接近时，这一项是最小化的，这通过它们的KL散度（KL Divergence）来衡量。

$q(x_{t-1}|x_t,x_0)$的具体数学表达可以由下图9的公式推理出来：

因此，我们已经证明，在每个步骤中， $x_{t-1}\sim q(x_{t-1}|x_t,x_0)$ 是正态分布的，其均值 ${\mu }_q(x_t,x_0)$ 是 $x_t$和 $x_0$ 的函数，而方差 ${\Sigma }_q(t)$ 是 $\alpha$ 系数的函数。这些 $\alpha$ 系数在每个时间步是已知的并且固定；它们要么在模型中作为超参数永久设定，要么被视为当前神经网络推理输出来建模它们。我们可以将方差方程重写为 ${\Sigma }_q(t)={\sigma }_q^2(t)I$，其中：${\sigma }_q^2(t)=\frac{(1-{\alpha }_t)(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}$
为了尽可能地将近似去噪转换步骤 $p_{\theta }(x_{t-1}|x_t)$ 与真实去噪转换步骤 $q(x_{t-1}|x_t,x_0)$ 匹配得更为接近，我们也可以将$p_{\theta }(x_{t-1}|x_t)$建模为高斯分布。此外，由于所有的 $\alpha$ 项在每个时间步都是已知的固定值，我们可以立即构建近似去噪转换步骤的方差，使其也为 ${\Sigma }_q(t)={\sigma }_q^2(t)I$。然而，由于 $p_{\theta }(x_{t-1}|x_t)$ 不以 $x_0$ 为条件，我们必须将它的均值 ${\mu }_{\theta }(x_t,t)$ 参数化为 $x_t$ 的函数。
然后如图10公式推导，可以得到一个时间步的损失函数。

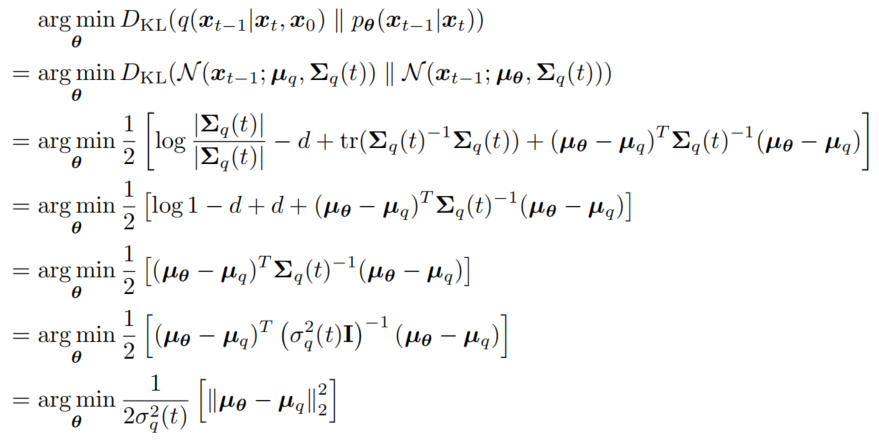
我们继续参数化。根据公式3变换可得公式7如下：
$x_0=\frac{x_t-\sqrt{1-\overline{{\alpha }_t}}{ϵ}_0}{\sqrt{{\bar{\alpha }}_t}}$ (7)

我们可以通过公式（7）消去${\mu }_q$的$x_0$，公式推导如图11所示：

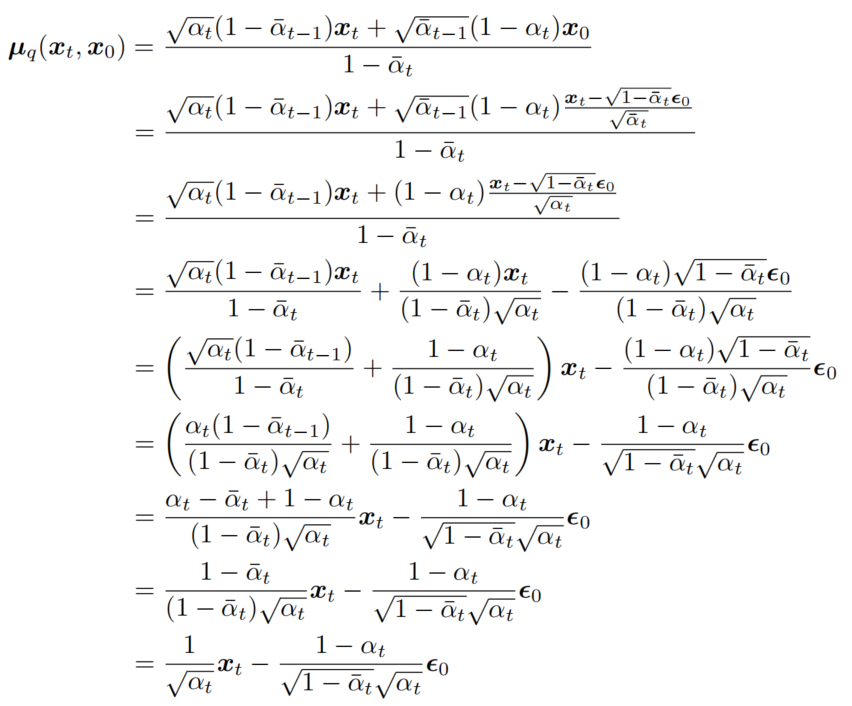
因此，我们可以将我们的近似去噪转移均值 ${\mu }_{\theta }(x_t,t)$ 设置为：
${\mu }_{\theta }(x_t,t)=\frac{1}{{\sqrt{\alpha }}_t}{x}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}\sqrt{{\alpha }_t}}{\widehat{ϵ}}_{\theta }(x_t,t)$ (8)
相应的优化问题变为：

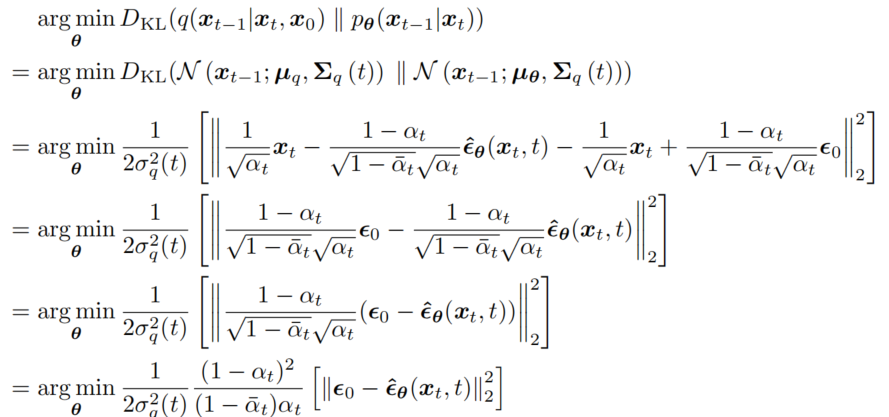
所以，我们最终的损失函数为:
$L_{t-1}=\arg {\min }_{\theta }{\mathbb{E}}_{x_0,ϵ}\frac{1}{2{\sigma }_q^2(t)}\frac{(1-{\alpha }_t{)}^2}{(1-{\bar{\alpha }}_t){\alpha }_t}[||{ϵ}_0-{\widehat{ϵ}}_{\theta }(x_t,t)|{|}_2^2],t\sim U(2,T)$ (9)。
对于重建项$L_0=\arg {\min }_{\theta }-{\mathbb{E}}_q\log p_{\theta }(x_0|x_1)$。在DDPM的原论文中，将这个生成过程的最后一项设置为了一个独立的离散编码器，由高斯分布$\mathcal{N}(x_0;{\mu }_{\theta }(x_1,1),{\sigma }^2\mathrm{I})$构成。具体而言，它将连续的高斯分布通过积分变换成离散的概率分布，用于计算给定条件 $x_1$ 下观测值 $x_0$ 的概率密度。展开$p(x_0|x_1)$如公式10所示，忽略常数和权重，我们只关注$||x_0-{\mu }_{\theta }(x_1,1)|{|}^2$。
$-\log p(x_0|x_1)=-\log \frac{1}{\sqrt{2\pi }{\sigma }_1^2}+\frac{||x_0-{\mu }_{\theta }(x_1,1)|{|}^2}{2{\sigma }_1^2}$ (10)
和之前的思路一样，消去$x_0$和重参数化，所以根据公式（7）得到$x_0=\frac{x_1-\sqrt{1-{\alpha }_1}{ϵ}_0}{\sqrt{{\alpha }_1}}$，根据公式（8）可以得到${\mu }_{\theta }(x_1,1)=\frac{1}{{\sqrt{\alpha }}_1}{x}_1-\frac{1-{\alpha }_1}{{\sqrt{1-\alpha }}_1\sqrt{{\alpha }_1}}{\widehat{ϵ}}_{\theta }(x_1,1)$，带入$||x_0-{\mu }_{\theta }(x_1,1)|{|}^2$得到：
$||x_0-{\mu }_{\theta }(x_1,1)|{|}^2=\frac{\sqrt{1-{\alpha }_1}}{\sqrt{{\alpha }_1}}||{ϵ}_0-{\widehat{ϵ}}_{\theta }(x_1,1)||\dots \dots 2$ (11)
忽略公式（9）和公式（11）的权重系数，我们可以得到最终化简的损失函数如公式（12）所示，且t取值为1到T：
$L_{simple}(\theta )={\mathbb{E}}_{t,x_0,ϵ}[||ϵ-{ϵ}_{\theta }(\sqrt{x_t},t)|{|}^2]={\mathbb{E}}_{t,x_0,ϵ}[||ϵ-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ,t)|{|}^2]$ (12)
这里，${\widehat{ϵ}}_{\theta }(x_t,t)$是一个神经网络，它学习预测源噪声${ϵ}_0\sim \mathcal{N}(ϵ;0,I)$，该噪声决定了从 $x_0$ 到 $x_t$ 的转变。这与我们直接上的理解是相同的。

代码编程

DDPM原论文伪代码如图13所示，分为训练和采样两个过程。需要注意的是采样阶段的第四行，对于$x_t$去噪得到$x_{t-1}$时加入了一个随机噪声${\sigma }_{t}z$。这样的目的是加入噪声扰动，是生成的数据更具多样性。

在所有实验中，DDPM原论文将T设为1000。将前向过程的方差设置为常数，从${\beta }_1=10^{-4}$线性增加到${\beta }_T=0.02$。选择这些常数时相对于缩放到$[-1,1]$范围的数据保持较小，以确保逆过程和前向过程具有大致相同的分布，同时使得在$x_T$处的信噪比尽可能小（在DDPM的实验中，$L_T=D_{KL}(q(x_T|x_0)||\mathcal{N}(0,I)\approx 10^{-5})$）。神经网络适用U-net模型。

这里给出labmlai实现的代码：

from typing import Tuple, Optional

import torch
import torch.nn.functional as F
import torch.utils.data
from torch import nn

from labml_nn.diffusion.ddpm.utils import gather

class DenoiseDiffusion:
    def __init__(self, eps_model: nn.Module, n_steps: int, device: torch.device):
        super().__init__()
        self.eps_model = eps_model #预测噪声的神经网络模型，比如u-net模型 
        self.beta = torch.linspace(0.0001, 0.02, n_steps).to(device) # n_steps，为总的时间步T，创建噪声beta
        self.alpha = 1. - self.beta  #beta为添加的噪声的方差
        self.alpha_bar = torch.cumprod(self.alpha, dim=0)
        self.n_steps = n_steps
        self.sigma2 = self.beta

    def q_xt_x0(self, x0: torch.Tensor, t: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]: 
        #获取q(x_t|x_0)分布的均值和方差
        mean = gather(self.alpha_bar, t) ** 0.5 * x0
        var = 1 - gather(self.alpha_bar, t)
        return mean, var

    def q_sample(self, x0: torch.Tensor, t: torch.Tensor, eps: Optional[torch.Tensor] = None):
        #q(x_t|x_0)分布的采样，使用重采样技巧
        if eps is None:
            eps = torch.randn_like(x0) #从标准正态分布采样一个样本
        mean, var = self.q_xt_x0(x0, t) #获取q(x_t|x_0)分布的均值和方差
        return mean + (var ** 0.5) * eps #返回从q(x_t|x_0)分布采样的样本

    
    def p_sample(self, xt: torch.Tensor, t: torch.Tensor):
        #从p(x_{t-1}|x_t)的分布中采样，生成过程
        eps_theta = self.eps_model(xt, t) #使用神经网络预测噪声
        alpha_bar = gather(self.alpha_bar, t)
        alpha = gather(self.alpha, t)
        eps_coef = (1 - alpha) / (1 - alpha_bar) ** .5
        mean = 1 / (alpha ** 0.5) * (xt - eps_coef * eps_theta) #采样伪代码中第四行右侧前半部分
        var = gather(self.sigma2, t) #采样伪代码中第四行右侧后半部分
        eps = torch.randn(xt.shape, device=xt.device)  
        return mean + (var ** .5) * eps #采样伪代码中第四行

    def loss(self, x0: torch.Tensor, noise: Optional[torch.Tensor] = None):
        batch_size = x0.shape[0]
        t = torch.randint(0, self.n_steps, (batch_size,), device=x0.device, dtype=torch.long)#伪代码1的第三行
        if noise is None:
            noise = torch.randn_like(x0) # 从标准正态分布提取样本，用于重参数化
        xt = self.q_sample(x0, t, eps=noise) # 返回从q(x_t|x_0)分布采样的样本
        eps_theta = self.eps_model(xt, t) # 伪代码1的第5行
        return F.mse_loss(noise, eps_theta)
        

:::info

参考文献

1. Denoising Diffusion Probabilistic Models
2. Understanding Diffusion Models: A Unified Perspective
3. Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song (yang-song.net)
4. What are Diffusion Models? | Lil’Log (lilianweng.github.io)
5. https://nn.labml.ai/diffusion/ddpm/index.html
6. https://github.com/labmlai/annotated_deep_learning_paper_implementations/tree/master
   :::