电机定义

电机是以磁场为媒介，利用电磁感应作用进行能量转换与传递的电磁装置。
机电能量转换装置，无论尺寸大小，从大型旋转电机如水轮发电机到小型机电信号变换器，虽然它们的用途和结构各异，但都基于相同的电磁场与运动载电物体（通常是载流导体）相互作用的基本原理。在机电装置中，当可动部分发生位移，导致装置内部耦合电磁场的储能发生变化时，通过耦合场的作用，电能与机械能之间可以相互转换。因此，机电能量转换装置通常包含载流的电系统（如绕组）、机械系统以及用作耦合和储存能量的电磁场，它们由一个固定部分和一个可动部分组成。机电能量转换是一个可逆的过程，这意味着大多数发电机可以作为电动机运行，反之亦然。

电机发展史

电机发展的历史，大体上可以分成 三个时期:
(1)直流电机的产生和形成时期;
(2)交流电机的形成和发展时期;
(3)电机理论、设计和制造 工艺逐步达到完善化的时期。

直流电机的产生和形成时期

1. 1821年 - 法拉第发现载流导体在磁场内受力的现象。
2. 1831年 - 法拉第发现电磁感应定律。
3. 1833年 - 楞茨证明电机的可逆原理。
4. 1834年 - 直流发电机开始发展，满足生产需要。
5. 1870年 - 直流发电机和电动机的可逆原理被接受，发展合而为一。
6. 1873年 - 海夫纳-阿尔泰涅克发明鼓形电枢绕组。
7. 1880年 - 爱迪生提出采用叠片铁心。
8. 1882年 - 台勃莱兹成功进行长距离直流电输送实验。
9. 1884年 - 出现换向极和补偿绕组。
10. 1885年 - 开始使用炭粉电刷。
11. 1886年 - 雀普金生兄弟确立磁路的欧姆定律。
12. 1891年 - 阿尔诺德建立直流电枢绕组理论。
13.19世纪末 - 直流电机具备了现代直流电机的主要结构特点，人们开始关注交流电

交流电机的形成和发展时期

1832年 - 单相交流发电机出现
1876年 - 亚勃罗契柯夫首次采用交流和开磁路式变压器给“电烛”供电
1884年 - 霍普金生兄弟发明了具有闭合磁路的变压器
1885年 - 齐波诺斯基、德利和勃拉第提出了变压器的芯式和壳式结构
1885年 - 弗拉利斯制成了第一台两相感应电动机
1888年 - 弗拉利斯提出了“利用交流电来产生电动旋转”的经典论文
1889年 - 多利伏-多勃罗伏尔斯基提出了三相制的建议，并设计和制出了三相感应电动机
1891年 - 建成了从劳芬到法兰克福的三相电力系统，显示三相交流电的优越性
1893年 - 开耐菜和司坦麦茨开始用复数和相量来分析交流电路
1894年 - 海兰特发表了“多相感应电动机和变压器性能的图解确定法”的论文
1894年 - 弗拉利斯采用双旋转磁场理论来分析单相感应电动机
1894年 - 波梯建立了交轴磁场理论
1899年 - 布朗台尔提出了双反应理论
19世纪末 - 各种交、直流电机的基本类型及其基本理论和设计方法大体上都已建立起来

电机理论、设计和制造工艺逐步达到完善化时期

20世纪初 - 水轮发电机的最大单机容量不超过1000kW，汽轮发电机的单机容量不超过500kW
1918年 - 福提斯古提出了求解三相不对称问题的一般方法——对称分量法
1926-1930年 - 道赫提和聂克尔在发展勃朗台尔双反应理论的基础上，发表了五篇经典论文
1929年 - 派克发表了“同步电机的双反应理论(1)—通用分析方法”的经典论文
1935-1938年 - 克朗提出了原型电机的概念，并利用张量分析来研究旋转电机
1920-1940年间 - 许多学者对双笼和深槽电机的理论和计算方法，谐波磁场所产生的寄生转矩及其削弱，感应电机的噪声等问题进行了一系列的研究
20世纪40年代前后 - 出现了一系列的控制电机，如电机放大器、交流测速发电机、旋转变压器等
1954年 - 柯伐煦提出了空间矢量法，并导出了感应电机的空间矢量电压方程
1957-1969年 - 卡佐夫斯基发表了一系列论文，提出用频率法来分析和求解交流电机的各种瞬态过程和非正常运行情况
1965年以后 - 计算机逐步被引入到电机工程的各个领域，先是模拟计算机，然后是数字计算机
1971年 - 勃拉舒克和海斯提出了交流电机的“矢量变换控制”
20世纪70年代以后 - 大电流晶闸管的发展，出现了便于控制、体积小、噪声小的大容量直流电源
20世纪80年代以后 - 永磁无刷电机和开关磁阻电机等新型电机得到较快的发展
20世纪90年代以后 - 一种场路结合的有限元一状态空间耦合时步法得到应用
20世纪末 - 电机理论和设计方法持续发展，计算机技术的进步使得电机的动态分析和设计更加精确。

电机学习框架

1. 建立物理模型：
   • 首先，了解电机的基本结构和主要部件的功能。
   • 分析电机的磁路和电路。
   • 研究空载和负载条件下电机内部的磁场、绕组中的电动势以及作用在转子上的电磁转矩。
   • 初步掌握电机的工作原理。
2. 建立数学模型：
   • 导出电机的运动方程，包括磁动势方程（或磁链方程）、电压方程和转矩方程。
   • 利用电磁学和动力学的基本定律，将电机内部的电磁过程和机电过程，用数学方程形式表达出来。
   • 这一步的目的是建立电机的数学模型，以便进行进一步的分析和计算。
3. 求解运动方程：
   • 根据问题的具体情况（如稳态、瞬态、对称或不对称运行等），确定合适的解法。
   • 求解运动方程可以采用解析解或数值解的方法，具体取决于问题的复杂性和可用的计算工具。
4. 结果分析：
   • 对求解结果进行分析，以确定电机的各种运行性能和主要运行数据。
   • 分析电机的额定数据、过载能力、稳定性、效率、电压变化率或速度变化率等性能指标。
   • 这一步的目的是满足解决日常工程问题的需要，并根据分析结果对电机的设计和运行进行优化。

以上四个步骤构成了电机学习的基本方法和框架，通过这些步骤，可以深入理解电机的工作原理、分析其性能，并解决实际工程中的问题。

理想电机能力模型

机电能量转换过程
机电能量转换过程是电场和磁场与运动的载电物体（通常为载流导体）相互作用的结果。当机电装置的可动部分发生位移，使装置内部耦合电磁场的储能发生变化，并在与之连接的电路系统和机械系统内产生一定的反应时，通过耦合场的作用，电能就会转换成机械能或反之。
机电能量转换装置的组成部分

1. 载流的电系统（绕组）：用于产生和传输电流。
2. 机械系统：用于产生和传递机械能。
3. 电磁场：用作耦合和储存能量的介质。

机电能量转换的特点

• 可逆性：大多数发电机可以作为电动机运行，反之亦然。
• 固定部分和可动部分：机电能量转换装置通常由固定部分和可动部分组成。

机电能量转换过程是电能和机械能之间相互转换的过程，它依赖于载流导体、机械系统和电磁场之间的相互作用。这种转换过程是可逆的，使得发电机和电动机在特定条件下可以互换使用。
绝大多数旋转电机都由电系统、机械系统和联系两者的耦合电磁场组成。其中电系统主要指定、转子绕组，绕组的出线端就是系统的电端又;机械系统主要指电机的转子，转轴则是系统的机械端又;耦合场可以是磁场，也可以是电场。考虑到在正常磁通密度和电场强度 下，单位体积内磁场的储能密度要比电场的储能密度大得多，所以绝大多数电机都以磁场作为耦合场。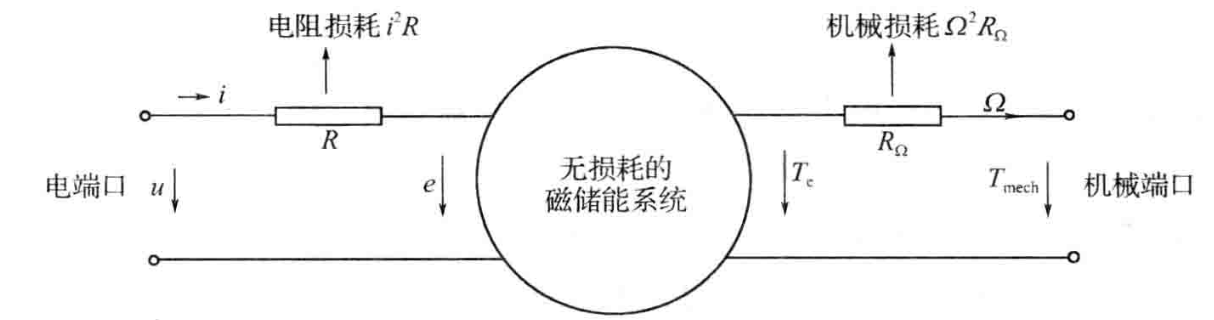

把电机作为一个具有电端又和机械端又的两端又装置，并把电阻损耗:$i^{2}R$从电系统中移出，其中R为绕组的电阻:转子的机械损耗${\Omega }^2{R}_{\Omega }$。从机械系统中移出，其中R。为机械阻力 系数;再把铁心损耗忽略不计;则装置的中心部分将成为 一个由无铁耗的铁心、气隙和无铜 粍、无机械损耗的动态耦合电路所组成的“无损耗的磁储能系统”。
电机能量模型可知，包括几个部分：
1.电能输入
2.感应电动势
3.磁能存储
4.电磁转矩
5.机械能输出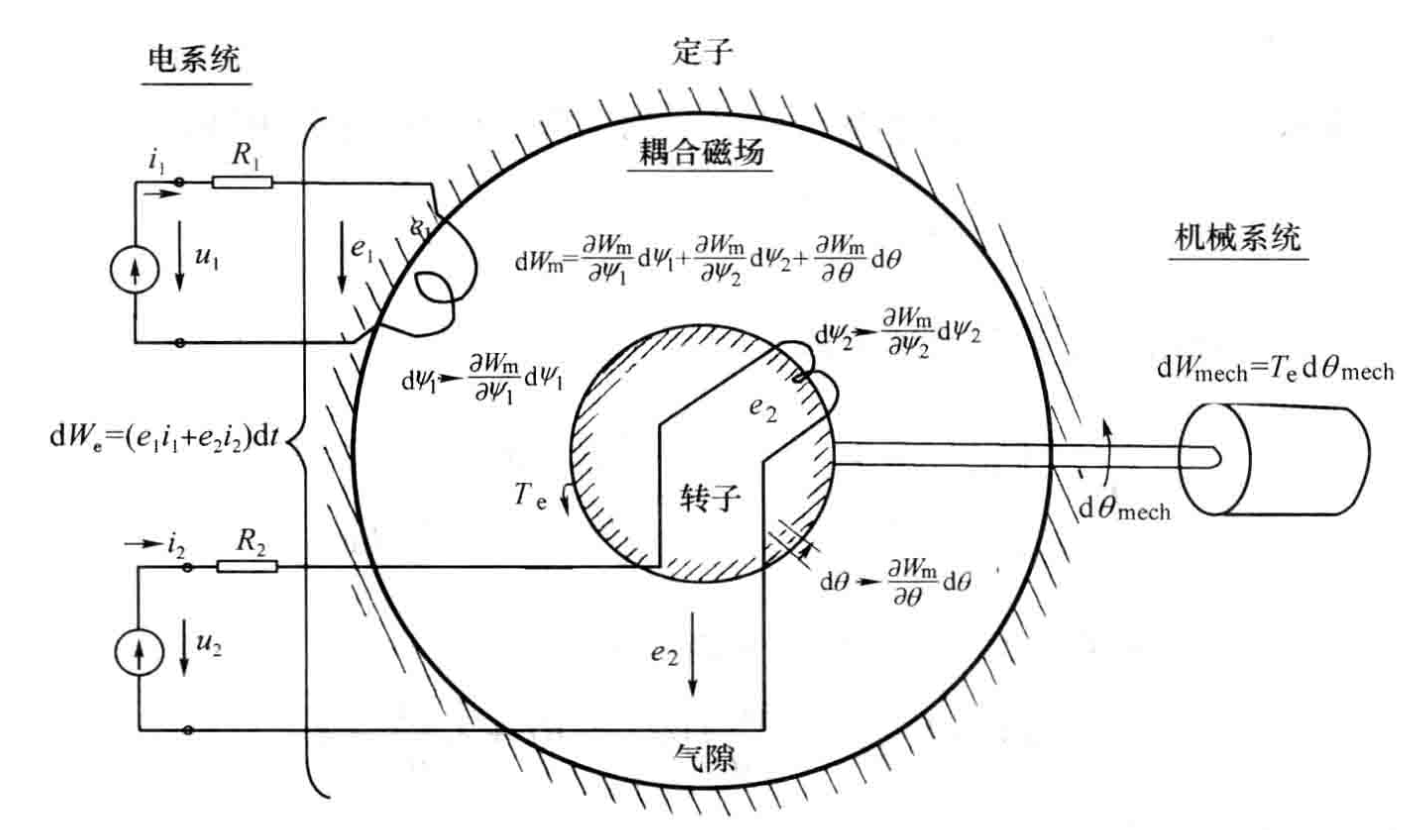

能量转换过程：
1.机电能量转化方程
2.电路方程
3.磁路方程
4.电磁转矩方程

转动电磁装置模型

单激励机电装置

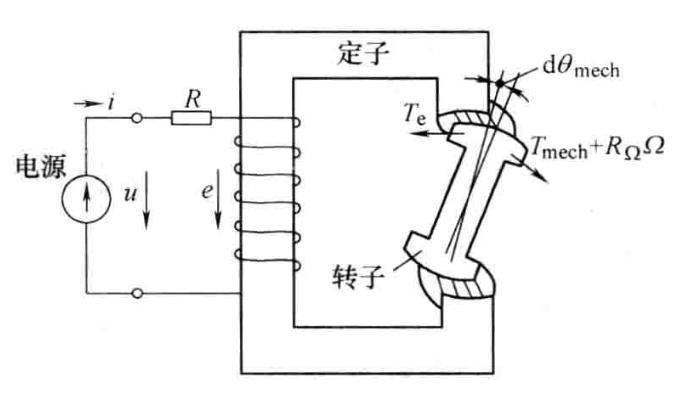
该装置由定子铁心、转子铁心和气隙组成一个闭电源合磁路，定 子铁心上装有一个绕组，该绕组与电源相连接，转子为凸极、不装绕组。这种装置的气隙主磁场 (耦合场)由定子电流所产生的磁动势单独激励而形成，故称为单激励装置。
电能输入
耦合场的磁场发生变化时，耦合场将对定子电路作出反应。设定子绕组的磁链为$\Psi$， 根据法拉第电磁感应定律，$\Psi$的变化将在定子绕组内感生电动势e
$e=\frac{d\Psi }{dt}$
在时间dt内，电源向电系统输人的微分净电能dwe
$$\begin{gathered} d{W}_e=(u-iR)idt \\ u-iR=-e,e=-\frac{d\Psi }{dt} \\ d{W}_e=-eidt=id\Psi \end{gathered}$$
机械能输出
$$\begin{gathered} d{W}_{mech}=(T_{mech}+R_{\Omega }\Omega )d\theta =T_{e}d{\theta }_{mech} \\ {T}_e=T_{mech}+R_{\Omega }\Omega \end{gathered}$$**磁场储能
$$\begin{gathered} d{W}_m=d{W}_e-d{W}_{mech}=id\Psi -T_{e}d{\theta }_{mech} \\ d{W}_m(\Psi ,\theta )=id\Psi -\frac{1}{p}{T}_{e}d\theta \\ \theta 是电角，和转角关系为：\theta =p{\theta }_{mech} \end{gathered}$$
磁能$W_m$是磁链$\Psi$和转角$\theta$两者的函数，即$W_m=W_m(\Psi ,\theta )$。所以从理论上 讲，如果已知电流i与磁链$\Psi$和转角$\theta$两者的关系$i(\Psi ,\theta )$，以及电磁转矩$T_e$与磁链$\Psi$和转角$\theta$两者的关系$T_e(\Psi ,\theta )$ 通 过 上 式 进 行 积 分 ， 即 可 求 出 磁链$\Psi$和转角的 终 值 达 到 磁链${\Psi }_0$和转角${\theta }_0$时 ， 耦 合 场 的 磁 能 $W_m({\Psi }_0,{\theta }_0)$， 即
$W_m({\Psi }_0,{\theta }_0)={\int }_{\Psi =0,\theta =0}^{{\Psi }_0,{\theta }_0}[i(\Psi ,\theta )d\Psi -\frac{1}{p}{T}_e(\Psi ,\theta )d\theta ]$
若磁路为线性，$\Psi -i$曲线是一条直线，$\Psi =L(\theta )i$,其中$L(\theta )$为定子绕组的自感，它仅是转角$\theta$的函数，此时$i=\Psi /L(\theta )$,于是
$$\begin{gathered} W_m(\Psi ,\theta )={\int }_0^{\Psi }i({\Psi }^{{}^{\prime }},\theta )d{\Psi }^{{}^{\prime }}={\int }_0^{\Psi }\frac{{\Psi }^{{}^{\prime }}}{L(\theta )}d{\Psi }^{{}^{\prime }}=\frac{1}{2}\frac{{\Psi }^2}{L(\theta )} \\ {W}_m(i,\theta )=\frac{1}{2}L(\theta )i^2 \end{gathered}$$
**电磁转矩 **
由于磁能$W_m$是磁链 $\psi$和转角$\theta$的函数，即$W_m=W_m(\psi ,\theta )$，所以磁能的全微分$d{W}_m$应为
$d{W}_m(\psi ,\theta )=\frac{\partial W_m}{\partial \psi }d\psi +\frac{\partial W_m}{\partial \theta }d\theta$
另一方面，
$d{W}_m(\psi ,\theta )=id\psi -T_{m}d\theta$
磁链 $\psi$和转角$\theta$是独立变量所以：
$i=\frac{\partial W_m(\psi ,\theta )}{\partial \psi }$
电磁转矩对应为：
$T_e=\frac{\partial W_m(\psi ,\theta )}{\partial {\theta }_{mech}}=-p\frac{\partial W_m(\psi ,\theta )}{\partial \theta }$
上式就是用系统的磁能表示时，电磁转矩的表达式。
当转子做微笑的角位移（可以使实际角位移，也可以使设想的虚角位移），如果系统的磁能同时发生变化，则转子上将受到电磁转矩的作用。电磁转矩的值等一磁能对转角的偏导数$\frac{\partial W_m(\psi ,\theta )}{\partial {\theta }_{mech}}$（磁链约束为常值），电磁转矩的方向为在恒磁链下趋势磁能减小的方向。
对于磁能为线性的情况，由于$W_m=\frac{1}{2}\frac{{\psi }^2}{L(\theta )}$，故用磁链$\psi$和转角$\theta$表示时，电磁转矩$T_e$应为
$T_e=-p\frac{\partial }{\partial \theta }(\frac{1}{2}\frac{{\psi }^2}{L(\theta )})=\frac{1}{2}p\frac{{\psi }^2}{L(\theta {)}^2}\frac{\partial L(\theta )}{\partial \theta }$
用电流和转角表示时也可以写成：
$T_e=\frac{1}{2}p{i}^2\frac{\partial L(\theta )}{\partial \theta }$

双激励机电装置

该装置中装有两个绕组：一个在定子上，另一个在转子上。它们分别接到各自的电源。由定、转子两边供电的装置也称为双馈装置。
电能输入
以定、转子绕组的磁链ψ₁、ψ₂和转子转角θ为自变量。当链过定、转子绕组的磁链发生变化时，两个绕组内将分别产生感应电动势e₁和e₂。
$e_1=-\frac{d{\psi }_1}{dt},e_2=-\frac{d{\psi }_2}{dt}$
设电源1和2向两个绕组输出的电流分别为$i_1和i_2$，则在时间$dt$内，扣除电阻上的损耗以后，从定、转子绕组输入装置的净电能$d{W}_e$应为：
$d{W}_e=-(e_1{i}_{1}dt+e_2{i}_{2}dt)=i_{1}d{\psi }_1+i_{2}d{\psi }_2$。
机械能输出
若转子的角位移引起耦合场内的磁能发生变化，则转子上将受到电磁转矩 ( $T_e$ ) 的作用。设时间 ( dt ) 内，转子的转角为 ( $d{\theta }_{mech}$)（机械角），电磁转矩为 ( $T_e$ )，则耦合场将向机械系统输出微分总机械能 ($d{W}_{mech}$)。
$d{W}_{mech}=T_{e}d{\theta }_{mech}=-T_{e}d\theta$
磁场储能
在时间 (dt) 内，系统磁能的微分增量 ($d{W}_m$) 应为：
$d{W}_m({\psi }_1,{\psi }_2,\theta )=d{W}_e-d{W}_{mech}=i_{1}d{\psi }_1+i_{2}d{\psi }_2-\frac{1}{P}{T}_{e}d\theta$
对式积分，可得磁链达到$({\psi }_{10})、({\psi }_{20})$，转角达到 (${\theta }_0$) 时的磁能$(W_m({\psi }_{10},{\psi }_{20},{\theta }_0))$为：
$W_m({\psi }_{10},{\psi }_{20},{\theta }_0)={\int }_{0,0,0}^{{\psi }_{10},{\psi }_{20},{\theta }_0}\left[i_1({\psi }_1,{\psi }_2,\theta )d{\psi }_1+i_2({\psi }_1,{\psi }_2,\theta )d{\psi }_2-\frac{1}{p}{T}_e({\psi }_1,{\psi }_2,\theta )d\theta \right]$
对于无损耗的磁储能系统，磁能$(W_m({\psi }_1,{\psi }_2,\theta ))$是一个状态函数，其值仅取决于磁链和转角的终值 $({\psi }_{10})、({\psi }_{20})和({\theta }_0)$，而与达到终值的路径无关，故可选择一条最简单的积分路径来求得$(W_m)$。
关键点：

1. 磁能微分增量由电能输入减去机械能输出得到。
2. 磁能可通过积分计算得到。
3. 磁能是状态函数，与路径无关。
4. 可选择简单路径进行积分计算。

对于磁路为线性的情况，磁链与电流之间为线性关系
$\{\begin{array}{l}{\psi }_1=L_{11}(\theta )i_1+L_{12}(\theta )i_2\\ {\psi }_2=L_{21}(\theta )i_1+L_{22}(\theta )i_2\end{array}$
式中，$(L_{11}(\theta ))和(L_{22}(\theta ))$分别表示定子和转子绕组的自感；$(L_{12}(\theta ))$ 表示定、转子绕组的互感$（L_{12}(\theta )=L_{21}(\theta )）$；它们仅与转子的角位置 $(\theta )$ 有关而与电流无关。式子可写成
$\{\begin{array}{l}{i}_1=\frac{L_{22}}{D}{\psi }_1-\frac{L_{12}}{D}{\psi }_2\\ i_2=-\frac{L_{21}}{D}{\psi }_1+\frac{L_{11}}{D}{\psi }_2\end{array}$
式中，$(D=L_{11}(\theta )L_{22}(\theta )-L_{12}^2(\theta ))$。把上式代入磁能表达式，即可导出磁路为线性时磁链$({\psi }_1)和({\psi }_2)$的表示式，两绕组系统的磁场储能为
$$\begin{gathered} W_m\left({\psi }_{10},{\psi }_{20},{\theta }_0\right)={\int }_0^{{\psi }_{10}}{i}_1\left({\psi }_1,0,{\theta }_0\right)d{\psi }_1+{\int }_0^{{\psi }_{20}}{i}_2\left({\psi }_{10},{\psi }_2,{\theta }_0\right)d{\psi }_2 \\ ={\int }_0^{{\psi }_{10}}{L}_{22}({\theta }_0)/D({\theta }_0){\psi }_{1}d{\psi }_1+{\int }_0^{{\psi }_{20}}[-L_{21}({\theta }_0)/D({\theta }_0){\psi }_{10}+L_{11}({\theta }_0)/D({\theta }_0){\psi }_2]d{\psi }_2 \\ =1/2L_{22}({\theta }_0)/D({\theta }_0){\psi }_{10}^2-L_{21}({\theta }_0)/D({\theta }_0){\psi }_{10}{\psi }_{20}+1/2L_{11}({\theta }_0)/D({\theta }_0){\psi }_{20}^2 \end{gathered}$$
在线性情况下，把式的ψ1和ψ2代入上式，经过整理，可得用电流i和转角θ表示时的磁能表达式为
$W_m(i_{10},i_{20},{\theta }_0)=1/2L_{11}({\theta }_0)i_{10}^2+L_{12}({\theta }_0)i_{10}{i}_{20}+1/2L_{22}({\theta }_0)i_{20}^2$
**电磁转矩 **
由于磁能是自变量${\psi }_1、{\psi }_2和{\theta }_0$三者的函数，所以用偏导数表示时，磁能的全微分$d{W}_m({\psi }_1,{\psi }_2,{\theta }_0)$为
$d{W}_m({\psi }_1,{\psi }_2,\theta )=\frac{\partial W_m({\psi }_1,{\psi }_2,\theta )}{\partial {\psi }_1}d{\psi }_1+\frac{\partial W_m({\psi }_1,{\psi }_2,\theta )}{\partial {\psi }_2}d{\psi }_2+\frac{\partial W_m({\psi }_1,{\psi }_2,\theta )}{\partial \theta }d\theta$
磁能的全微分$d{W}_m$为
$d{W}_m({\psi }_1,{\psi }_2,\theta )=i_{1}d{\psi }_1+i_{2}d{\psi }_2-\frac{1}{P}{T}_{e}d\theta$
把上面这两个式子加以比较，可知
$i_1=\frac{\partial W_m({\psi }_1,{\psi }_2,\theta )}{\partial {\psi }_1},i_2=\frac{\partial W_m({\psi }_1,{\psi }_2,\theta )}{\partial {\psi }_2},T=-\frac{\partial W_m({\psi }_1,{\psi }_2,\theta )}{\partial {\theta }_{mech}}=-p\frac{\partial W_m({\psi }_1,{\psi }_2,\theta )}{\partial \theta }$
就是用磁能表示时，双激励机电装置中电磁转矩的表达式。不难看出，此式与单激励装置中的式是一致的，只不过此处$W_m是{\psi }_1、{\psi }_2和{\theta }_0$三个自变量的函数。
对于磁路为线性的情况，即可得到用$i和\theta$表示时电磁转矩的表达式为
$T_e=p\left(\frac{1}{2}\frac{\partial L_{11}(\theta )}{\partial \theta }{i}_1^2+\frac{\partial L_{12}(\theta )}{\partial \theta }{i}_1{i}_2+\frac{1}{2}\frac{\partial L_{22}(\theta )}{\partial \theta }{i}_2^2\right)$
式中的第一项和第三项是由定子、转子电流和各自的自感随转角$\theta$的变化所引起，称为磁拉转矩；第二项是由定子、转子电流和它们的互感随转角$\theta$的变化所引起，称为磁拉转矩。此式既简便，物理意义又比较清楚，所以在工程上得到广泛的应用。

转动电磁装置能量转化

机电能量转化过程

从上节的分析可知，双激励装置在时间d内，有如下的微分能量关系: 净电能输入
$d{W}_e=i_{1}d{\psi }_1+i_{2}d{\psi }_2$
耦合场内磁能的变化
$$\begin{gathered} d{W}_m=(\frac{\partial W_m}{\partial {\psi }_1}d{\psi }_1+\frac{\partial W_m}{\partial {\psi }_2}d{\psi }_2)+\frac{\partial W_m}{\partial \theta }d\theta \\ =i_{1}d{\psi }_1+i_{2}d{\psi }_2-T_{e}d{\theta }_{mech} \end{gathered}$$
总机械能输出
$d{W}_{mech}=T_{e}d{\theta }_{mech}$
对于耦合场，以输入能量为正，输出为负。从上述关系可见，磁能的增量$d{W}_m$包括两部分:
其中由磁链变化所引起的磁能增量($\frac{\partial W_m}{\partial {\psi }_1}d{\psi }_1+\frac{\partial W_m}{\partial {\psi }_2}d{\psi }_2$)，恰好等于从电源吸收的净电能$d{W}_e$;
另一部分由转子角位移的变化所引起的磁能增量$\frac{\partial W_m}{\partial \theta }d\theta$，则恰好等于输出的微分机械能$d{W}_{mech}$的负值。
在能量转换过程中，作为耦合场的磁场既可以从电系统输入或输出能量，也可以对机械系统输出或输入能量，其状态主要取决于对磁链ψ和转子的角位移θ所加的约束:
(1) 若装置的转子静止不动，$d{\theta }_{mech}=0$$d{W}_{mech}=0$，于是$d{W}_m=d{W}_e$。此时没有机械能输出，通过磁链的变化从电系统输入的电能，将全部转换为耦合场内的磁能。
(2) 若装置的磁链不变，$d\psi =0$$，则$$d{W}_e=0$$-d{W}_m=d{W}_{m}ech$。此时装置无电能输入，随着转子的转动，磁能将逐步释放出来变为输出的机械能。
(3) 两者同时存在变化的情况，一方面磁链发生变化，另一方面转子又有角位移，此时电角位移所引起的磁能变化将产生电磁力，并使部分磁场储能释放出来变为机械能; 由磁链变化所引起的磁能变化，将通过线圈内的感应电动势从电源输入等量的电能而不断地得到补充。这样，通过耦合磁场的作用，电能将不断地转换为机械能或反之。
总之，机电能量转换过程是以气隙中的耦合磁场为中心，从电能转换为磁能，再从磁能转换为机械能的过程(或反之)。其中感应电动势和电磁转矩分别是耦合场与电系统和机械系统之间的一对耦合项。如果没有耦合磁场，或者耦合场不具备这种特定的性质，即磁场储能发生变化时会对电系统和机械系统作出一定的反应(即产生感应电动势和电磁转矩)，使电能输入、机械能输出，则机电能量间的转换就无法实现。
剩下一个环节是，在气隙内部电磁能量是如何从定子传送到转子的。研究表明，在气隙内部，主要是通过坡印廷能流向量的径向分量，把电磁能量从定子传送到转子。

功率方程

下面进一步列出能量转换过程中的功率关系。为简化分析，假定磁路为线性电压方程 设定、转子绕组的端电压分别为 u₁ 和 u₂，电流为 i₁ 和 i₂，磁链为 ψ₁ 和 ψ₂，
则当 ψ₁ 和 ψ₂ 随时间变化时，定、转子绕组内将产生感应电动势 e₁ 和 e₂，e₁ = - dψ₁/dt，e₂ =-dψ₂/dt。若磁路为线性，ψ₁、ψ₂ 与电流 i₁、i₂ 的关系为
ψ₁ = L₁₁(θ)i₁ + L₁₂(θ)i₂
ψ₂ = L₂₁(θ)i₁ + L₂₂(θ)i₂
于是
e₁ = - dψ₁/dt = - (L₁₁ di₁/dt + L₁₂ di₂/dt) - (i₁ ∂L₁₁/∂θ + i₂ ∂L₁₂/∂θ) dθ/dt
e₂ = - dψ₂/dt = - (L₂₁ di₁/dt + L₂₂ di₂/dt) - (i₁ ∂L₂₁/∂θ + i₂ ∂L₂₂/∂θ) dθ/dt
式中，右端的第一部分是由电流变化所引起，称为变压器电动势，用 e₁ᴛ 和 e₂ᴛ 表示；第二部分是由转子的旋转运动所引起，其大小与转子旋转的角速度 dθ/dt 有关，称为运动电动势，用 e₁ₙ 和 e₂ₙ 表示。若定、转子绕组的电阻分别为 R₁ 和 R₂，根据基尔霍夫第二定律，可知定、转子绕组的电压方程为
u₁ = i₁R₁ - e₁ = i₁R₁ + (L₁₁ di₁/dt + L₁₂ di₂/dt) + (i₁ ∂L₁₁/∂θ + i₂ ∂L₁₂/∂θ) ωᵣ
u₂ = i₂R₂ - e₂ = i₂R₂ + (L₂₁ di₁/dt + L₂₂ di₂/dt) + (i₁ ∂L₂₁/∂θ + i₂ ∂L₂₂/∂θ) ωᵣ
式中 (${\omega }_r$) 为转子的电角速度，(${\omega }_r=\frac{d\theta }{dt}$) 是否存在运动电动势，是动态电路和静止电路的重要电机学区别之一。
$u=\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right],i=\left[\begin{array}{c}{i}_1\\ i_2\end{array}\right]$
用矩阵表示时，若 ( u ) 为定、转子绕组的电压列矩阵，( i ) 为电流列矩阵，( R ) 和 ( L ) 为定、转子绕组的电阻和电感矩阵，
$R=\left[\begin{array}{cc}{R}_1& 0\\ 0& R_2\end{array}\right],L=\left[\begin{array}{cc}{L}_{11}(\theta )& L_{12}(\theta )\\ L_{21}(\theta )& L_{22}(\theta )\end{array}\right]$
则两个电压方程可简写成一个矩阵方程，即
$u=Ri+L\frac{di}{dt}+(\frac{\partial L}{\partial \theta }i){\omega }_r=Ri+L\frac{di}{dt}-e_{\Omega }$
其中 ($e_{\Omega }$) 为运动电动势矩阵，
$e_{\Omega }=-\left[\begin{array}{c}\left(\frac{\partial L_{11}}{\partial \theta }{i}_1+\frac{\partial L_{12}}{\partial \theta }{i}_2\right)\\ \left(\frac{\partial L_{21}}{\partial \theta }{i}_1+\frac{\partial L_{22}}{\partial \theta }{i}_2\right)\end{array}\right]{\omega }_r=-(\frac{\partial L}{\partial \theta }i){\omega }_r$

功率方程

把式中的第一式乘以 ( i_1 )，第二式乘以 ( i_2 )，然后相加，可得该装置的功率方程
$u_1{i}_1+u_2{i}_2=(R_1{i}_1^2+R_2{i}_2^2)+(L_{11}{i}_1\frac{d{i}_1}{dt}+L_{12}{i}_1\frac{d{i}_2}{dt})+(L_{21}{i}_2\frac{d{i}_1}{dt}+L_{22}{i}_2\frac{d{i}_2}{dt})++(i_1^2\partial L_{11}/\partial \theta +i_1{i}_2\partial L_{12}/\partial \theta ){\omega }_r+(i_1{i}_2\partial L_{21}/\partial \theta +i_2^2\partial L_{22}/\partial \theta ){\omega }_r$
用矩阵表示时有
$i^{T}u=i^{T}Ri+i^{T}Ldi/dt-i^T{e}_{\Omega }$
式中，$i^T$ 表示 i 的转置矩阵。磁路为线性时，磁能$W_m$为
$W_m=1/2L_{11}(\theta )i_1^2+L_{12}(\theta )i_1{i}_2+1/2L_{22}(\theta )i_2^2$
磁能随时间的变化率$d{W}_m/dt$应为
$d{W}_m/dt=(L_{11}{i}_1+L_{12}{i}_2)d{i}_1/dt+(L_{21}{i}_1+L_{22}{i}_2)d{i}_2/dt+(1/2i_1^2\partial L_{11}/\partial \theta +i_1{i}_2\partial L_{12}/\partial \theta +1/2i_2^2\partial L_{22}/\partial \theta ){\omega }_r=i^{T}Ldi/dt-1/2i^T{e}_{\Omega }$
说明，在线性情况下，耦合场内磁能随时间的变化率，应当等于被变压器电动势所吸收的瞬时功率，加上被运动电动势所吸收的瞬时功率的二分之一。
对应于磁能转换为机械能的这部分功率，通常称为转换功率。不难看出，转换功率$P_{\Omega }$应为
$P_{\Omega }=\frac{(-\partial W_m({\psi }_1,{\psi }_2,\theta )/\partial \theta )d\theta }{dt}=-\partial W_m({\psi }_1,{\psi }_2,\theta )/\partial \theta \cdot {\omega }_r=T_e\Omega$

即转换功率就等于输出的总机械功率,对稳态和瞬态都成立。再把电磁转矩的表达式代入，可得
$P_{\Omega }=(1/2i_1^2\partial L_{11}/\partial \theta +i_1{i}_2\partial L_{12}/\partial \theta +1/2i_2^2\partial L_{22}/\partial \theta ){\omega }_r=-1/2(e_{1\Omega }{i}_1+e_{2\Omega }{i}_2)=-1/2i^T{e}_{\Omega }$
说明，只有绕组中存在运动电动势时，才会产生机电能量转换；转换功率等于所有绕组中的运动电动势所吸收的功率的 1/2。
最后，把功率方程中的$i^T{e}_{\Omega }$分成两项，可得
$\underset{\text{输入的电功率}}{\underbrace{i^{T}u}}=\underset{\text{电阻损耗}}{\underbrace{i^{T}Ri}}+\underset{\text{耦合场内磁能的变化率}}{\underbrace{i^{T}Ldi/dt-1/2i^T{e}_{\Omega }}}-\underset{\text{转换功率}}{\underbrace{1/2i^T{e}_{\Omega }}}$
表明：装置从电源输入的电功率，部分将用以克服绕组内的电阻损耗，部分成为耦合场内磁能的变化率，最后一部分成为转换功率并变成机械功率输出。

转动电磁装置能量转化条件

机电能力转化的条件

若要持续地进行机电能量转换，在一转内，转换功率的平均值应当不等于零，即
$-\frac{1}{2}(i^T{e}_{\Omega }{)}_{av}=(T_e\Omega {)}_{av}\ne 0$
为此，转子的机械角速度$\Omega$不能为零，即机电能量之间的转换必定在转子旋转的过程中进行；另外，运动电动势$e_{\Omega }和电磁转矩的平均值T_{e(av)}$也不能等于0。稳态运行时，$\Omega =常值$，转子转过一周，装置中的磁链$\psi 和转角\theta$的值与一周前相同，所以作为状态函数的磁能$W_m$，其值应与一周前相同，或者说，转子转过一周，磁能的变化量为0，即
$(\frac{d{W}_m}{dt}{)}_{av}=(i^{T}L\frac{di}{dt}-\frac{1}{2}{i}^T{e}_{\Omega }{)}_{av}=0$
两式要求：
(1) 定、转子绕组的极数必须相等，否则电磁转矩的平均值将等于0。
(2) 对双激励装置，在线性情况下，因为
$T_e(av)=p(1/2i_1^2\partial L_{11}/\partial \theta +i_1{i}_2\partial L_{12}/\partial \theta +1/2i_2^2\partial L_{22}/\partial \theta {)}_{a}v$
所以$\partial L_{1}1/\partial \theta 、\partial L_{2}2/\partial \theta 和\partial L_{1}2/\partial \theta$不能都等于0。若这三个量都等于0，则转子的转角变化时，磁能将不发生变化，于是电磁转矩将等于0，从而无法实现机电能量之间的转换。所以构造以磁场为耦合场的旋转电机时，要注意定、转子绕组的各个电感是否随转角θ的变化而变化。∂L/∂θ愈大，同样电流下，电磁转矩就愈大。
(3) 定、转子绕组内的电流必须全部是交流，或者有的是交流，有的是直流，而不能全部是直流。如果全部是直流，di/dt = 0，$1/2(i^T{e}_{\Omega }{)}_{a}v=0$，转换功率的平均值就等于0，装置中就不会有机电能量间的转换。
(4) 定、转子电流的角频率与转子旋转的角速度Ω之间，要满足一定的约束（称为频率约束）。下面进一步来研究此问题。

定转子电流频率约束

下面分成隐极和凸极电机两种情况来说明。

隐极电机的频率约束

对于隐极电机，不计齿、槽影响时，定、转子之间的气隙是均匀的，所以无论转子转到什么位置，定子和转子的自感均为常值，即
L₁₁ = 常值 L₂₂ = 常值 ∂L₁₁/∂θ = ∂L₂₂/∂θ = 0
于是磁阻转矩为零，电磁转矩中仅有主电磁转矩，
Tₑ = pi₁i₂ ∂L₁₂/∂θ
设定、转子绕组之间的互感L₁₂随转子转角θ的余弦而变化，即
L₁₂ = Mcosθ
式中，M为定、转子绕组轴线重合时（即θ=0时）互感的幅值。再设定、转子绕组分别通有角频率为ω₁和ω₂的正弦交流，即
i₁ = √2I₁cos(ω₁t + φ₁) i₂ = √2I₂cos(ω₂t + φ₂)
考虑到θ=pΩt+θ₀，θ₀为t=0时转子的初相角，可得
Tₑ = -p√2I₁cos(ω₁t + φ₁)√2I₂cos(ω₂t + φ₂)Msinθ
= -pI₁I₂M{cos[(ω₁ + ω₂)t + φ₁ + φ₂] +
cos[(ω₁ - ω₂)t + φ₁ - φ₂]}sin(pΩt + θ₀)
根据正弦函数的正交性，两个正弦函数相乘，仅当它们的频率相等时，其乘积在一个周期内的平均值才不等于零，因此仅当
pΩ = ± (ω₁ ± ω₂)
时，电磁转矩的平均值才不等于零。就是持续进行机电能量转换时，凸极电机定、转子电流所需满足的频率约束。
可见，对于凸极电机，若定子和转子电流的角频率ω₁和ω₂中有一个是可变的，则电机可在不同的角速度 Ω 下进行机电能量转换。

凸极电机的频率约束

若转子为凸极，则转子绕组的自感 L22 仍然与转角 θ 无关，定、转子绕组间的互感 L12 。
L22 = 常值 L12 = Mcosθ
定子绕组的自感 L11 则近似等于一个恒定分量 Ls0 与一个随 cos2θ 而变化的二次谐波分量
Ls2cos2θ 之和，即
L11 ≈ Ls0 + Ls2cos 2θ
若定、转子电流 i1 和 i2 的表达式：
i₁ = √2I₁cos(ω₁t + φ₁) i₂ = √2I₂cos(ω₂t + φ₂) ，
则此时除主电磁转矩外，还将出现一个仅与定子激励有关的磁阻转矩 Te(s)，其中主电磁转矩
Tₑ = -p√2I₁cos(ω₁t + φ₁)√2I₂cos(ω₂t + φ₂)Msinθ
= -pI₁I₂M{cos[(ω₁ + ω₂)t + φ₁ + φ₂] +
cos[(ω₁ - ω₂)t + φ₁ - φ₂]}sin(pΩt + θ₀)
，磁阻转矩 Te(s)则等于
$Te(s)=1/2p{i}_1^2\partial L_{11}/\partial \theta =-2p{I}_1^2{L}_{s2}co{s}^2({\omega }_{1t}+{\phi }_1)sin2\theta =-p{I}_1^2{L}_{s2}[1+cos2({\omega }_{1t}+{\phi }_1)]sin2(p\Omega t+{\theta }_0)$
根据正弦函数的正交性，此转矩仅在余弦项中的角频率 ±2ω1 与正弦项中的角频率 2pΩ 相
等，即
pΩ = ± ω1
时才具有不等于零的平均值。可见，对于凸极电机，为使磁阻转矩和主电磁转矩都能发挥作用，电机只能在与ω1相对应的同步转速下运行。
若定、转子两边都是凸极结构，则与L11相类似，转子绕组的自感L22也将近似地等于一个恒定分量 Lr0 和一个二次谐波分量 Lr2cos2θ 之和，即
L22 ≈ Lr0 + Lr2cos2θ
此时磁阻转矩中除了包含与定子激励有关的分量 Te(s) 外，还将包含一个与转子激励有关的分量 Te®，
$T_e(r)=p1/2i_2^2\partial L_{22}/\partial \theta =-p{I}_2^2{L}_{r2}[1+cos2({\omega }_{2}t+{\phi }_2)]sin2(p\Omega t+{\theta }_0)$
此转矩仅在
$p\Omega =\pm {\omega }_2$
时才有不等于零的平均值，于是电机将出现第二个同步转速。实际上，电机仅能在某一个转速下运行，因而磁阻转矩的两个分量中必有一个成为平均值等于零的脉振转矩，从而将引起不希望有的转矩振荡。所以实用中，以正弦电流供电的"旋转磁场式"电机，很少采用双边凸极式结构；对于由脉冲电流供电的电动机（例如开关磁阻电机），有时会采用这种结构。

各电机频率约束

直流电机 直流电机的定子绕组中通有直流励磁电流，故角频率 ω1 = 0；转子电刷出线端呈为直流，但是由于换向器的变频作用，电枢线圈内的电流却是交流，其频率 f2 = pn/60，即 ω2 = 2πf2 = pΩ，故能满足定子为凸极边时的频率约束
pΩ = ± (ω1 ± ω2) pΩ = ± ω2
由于转子电流的角频率 ω2 随着转速的变化而自动变化，所以直流电机在任何转速下均能持续地进行机电能量转换。
同步电机 对旋转磁极式同步电机，转子通入直流励磁电流，故 ω2 = 0；定子若接到电网，定子电流频率 f1 = pns/60，即 ω1 = 2πf1 = pΩs；所以仅在同步转速下才能满足凸极电机的频率约束
pΩ = ± (ω1 ± ω2) pΩ = ± ω1
换言之，接于电网的同步电机，仅在同步转速下才能持续地进行机电能量间的转换。若为单独运行，由于定子电流的频率随着转速的变化而自动变化，故在任何转速下均能满足频率约束并进行能量转换。
感应电机 感应电机定子电流的频率为电源频率 f1，故 ω1 = 2πf1；转子电流的频率为转差频率 ω2 = sω1，转子的机械角速度 Ω = Ωs (1 - s)；所以
pΩ = pΩs(1 - s) = ω1 - ω2
上式表明，由于转子电流由感应而生，其频率随着转子转速的变化而自动变化，所以感应电机在任何转速下都能满足频率约束，并持续地进行能量转换。
双馈电机 若感应电机为绕线型转子，转子边接到转差频率的变频电源，则电机将成为定、转子双边激励的双馈电机。不难看出，改变转子变频电源的频率，转子的转差率（转速）就将发生变化，从而达到调速的目的。
总之，当满足频率约枣时，定、转子电流所产生的磁动势(磁场)在空间将始终保持 相对静止。所以实现机电能量转换的第四个条件也可以表示为:定、转于要有相对运动， 定、转子电流所产生的磁动势则应保持相对静止。

小结

要实现机电能量转换，机电装置中首先要有耦合场和与之关联的电磁系统和机械系统。 耦合场可以是电场，也可以是磁场。由于在正常的磁通密度和电场强度下，单位体积内空气 中的磁场储能要比电场储能大得多，所以实用的电机都以磁场作为耦合场 。其次，耦合场必 须具备特定的性质，即耦合场的储能发生变化时 ，能在所连接的电系统和机械系统中产生相 应的反应，即出现机电耦合项，例如在绕组中产生感应电动势，在转子上产生电磁转矩 。所 以，确定磁场储能、确定感应电动势和电磁转矩，是研究机电能量转换过程的先导。
无损耗磁储能系统模型

• 磁能公式: 建立一个模型使得磁能 ( W ) 成为磁链 ( \Phi ) 和转角 ( \theta ) 的单值函数。这意味着 ( W ) 的值由 ( \Phi ) 和 ( \theta ) 的即时值唯一确定。
• 状态变量: ( \Phi ) 和 ( \theta ) 成为系统的状态变量，而磁能 ( W(\Phi, \theta) ) 则成为表征系统状态的状态函数。
• 状态函数性质: 状态函数的值与达到该状态的路径无关。

磁能公式的推导

• 最简单路径: 由于状态函数的性质，可以通过最简单的路径来导出磁能公式。
• 能量守恒原理: 利用能量守恒原理和磁能的全微分性质，可以导出电磁转矩的表达式。
• 线性情况下的表达式: 在线性情况下，磁能和电磁转矩可以用电感 ( L(\theta) ) 和电流 ( i ) 表达。

电磁转矩的计算

• 通用方法: 通过磁能对转角的偏导数来确定电磁转矩，这种方法不需要考虑电磁力的具体分布。
• 特殊情况: 对于装置结构特殊或绕组内电流非正弦波的情况，这种方法非常有用。

机电能量转换过程

• 电动机: 输入的电能首先转换为耦合场的磁能，再从磁能转换为机械能输出。
• 发电机: 过程与电动机相反。
• 稳态情况: 在稳态下运行时，转子每转一周，磁能变化量为零，因此输入的电能等于输出的机械能。
• 瞬态情况: 瞬态时，耦合场内的磁能发生变化，输入电能与输出机械能不再相等。

机电能量转换的条件

1. 极数相等: 定子和转子的极数必须相等。
2. 自感和互感: 定子和转子绕组的自感和互感对转角的偏导数不能都为零。
3. 电流类型: 绕组中的电流必须全部是交流，或一部分交流一部分直流，但不能全部是直流。
4. 频率约束: 定子和转子电流的频率需满足特定约束，确保定子和转子产生的磁场保持相对静止。

这些条件是在设计和实际运行电机时必须遵循的基本要求。