给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/示例 :
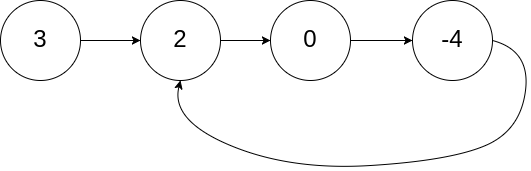
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
思路
沉淀,又是被白袜体育生扣圈的一天。
试想:如果路径在某一处成环,在起点释放一个快指针和一个慢指针,他们必定在不同时刻入环,之后必定在某一刻相遇。
算法过程
两个速度不同的指针从起点开跑,如果有环,两指针分别在不同时刻入环,慢指针入环后必被快指针扣圈。
Floyd判环算法,也称龟兔赛跑算法,可用于判断链表、迭代函数、有限状态机是否有环。如果有,找出环的起点和大小。时间复杂度O(n),空间复杂度O(1)。
此处以链表为例, 定以慢指针slow,每次走一步:slow=slow->next;,快指针fast,每次走两步:fast=fast->next->next;
路线分析:
s=从直线起点到环入口的距离,m=环周长。
两指针相遇时,他们走过的路程之差总是环周长的整数倍:慢指针走了s+qm,快指针走了s+pm(p>q)这是由于快指针要比慢指针走更多完整圈数才能在相同慢指针行进的某一圈上与之相逢。
相遇失败(false或false的next变成空指针)返回fasle,否则返回true。
复杂度
时间复杂度: O(s+m)
空间复杂度: O(1)s:从直线起点到环入口的距离
m:环周长
复杂度分析:为什么时间复杂度后半部分是m?通常,定义slow一次一步,fast一次两步。假设同时入环,当fast走完1圈,slow走了1/2圈;当fast走3/2圈,slow走3/4圈;当fast走2圈slow走1圈。
正常来讲,除非环在起点,否则两指针不可能同时入环,两指针相逢的时间总是km级别的(k是常数)所以
Code
class Solution {
public:
bool hasCycle(ListNode *head) {
if(!head||!head->next)return false;
ListNode *slow=head;
ListNode *fast=head->next;
while(slow!=fast){
if(!fast||!fast->next)return false;
slow=slow->next;
fast=(fast->next)->next;
}
return true;
}
};


















