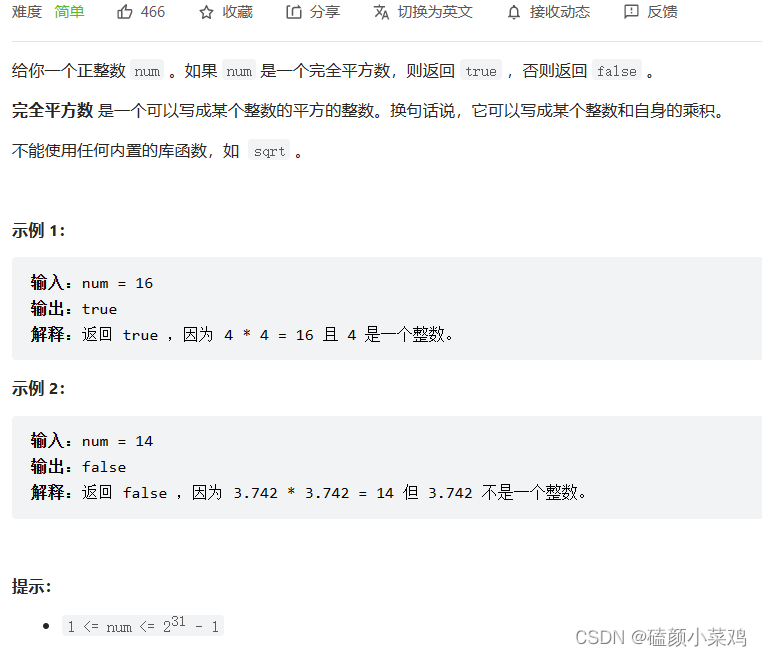
路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]

输出：6

解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

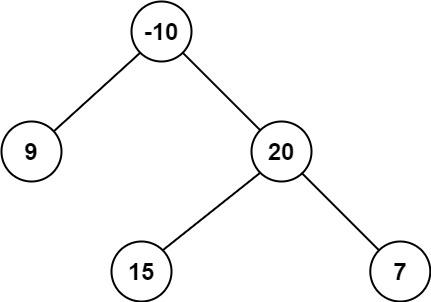
输入：root = [-10,9,20,null,null,15,7]

输出：42

解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

124. 二叉树中的最大路径和 - 力扣（Leetcode）

思路：

用递归方法，本题属于后续遍历，即先递归处理左右两个孩子节点，再处理当前节点
定义 函数 maxSum(TreeNode root) ，该函数意义为返回以该节点作为路径中一员，其能提供的最大贡献为 maxSum
处理当前节点的逻辑：
1. 以当前节点为根节点所能获取的最大路径和。若是左右子节点能提供的最大贡献大于 0 ，则可以将左右子节点加入到路径中
2. 返回当前节点能提供的最大路径和，结果为 root.val + max(leftSum, rightSum)

c++:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int result = 0;
    int maxPathSum(TreeNode* root) {
        if(root == nullptr) {
            return 0;
        }
        // 获取二叉树中值最小的节点，并以此为基础，进行比较
        dfs(root);
        
        maxSum(root);

        return result;
    }
    
    // 该函数意义为返回 当前节点 root 所能返回的最大贡献值
    int maxSum(TreeNode* root) {
        if(root == nullptr) {
            return 0;
        }
        int leftSum = maxSum(root->left);
        int rightSum = maxSum(root->right);
                
        leftSum = max(leftSum, 0);
        rightSum = max(rightSum, 0);

       // 以当前节点为根节点的路径最大和
        result = max(result, root->val + leftSum + rightSum);

        // 当前节点作为路径中的一个节点，所能贡献的最大值
        return root->val + max(leftSum, rightSum);
    }

    void dfs(TreeNode* root) {
        if(root == nullptr) {
            return;
        }
        if(result>root->val) {
            result = root->val;
        }
        dfs(root->left);
        dfs(root->right);
    }

};