1.1 数组基础理论
(1)定义:数组是存储在连续内存空间上相同类型数据的集合。
(2)注意:
- 数组下标是从0开始的;
- 数组在内存空间的地址是连续的。
=>删除或增添数组元素难免要移动其他元素的地址
(3)数组中的元素不能删除,只能覆盖
1.2 二分查找
1.2.1 二分法介绍
(1)使用前提:数组元素是有序的。
(2)时间复杂度:O (log N)
(3)二分法的区间定义有两种:左闭右闭 [left, right] 和 左闭右开 [left, right)
- 左闭右闭 [left, right]
前提边界条件设置:
int left = 0;
int right = numsSize - 1; //尤其注意这里
有两点要注意:
while (left <= right) // 注意这里是 <=
if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid + 1; // 注意这里有 + 1
else
return mid;
- 左闭右开 [left, right)
前提边界条件设置:
int left = 0;
int right = numsSize; // 注意这里没有进行 - 1
有两点要注意:
while (left < right) // 注意这里只是 <
if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid; // 注意这里没有进行 + 1
else
return mid;
1.2.2 相关题目推荐
704、二分查找

- 左闭右闭
int search(int* nums, int numsSize, int target){
int left = 0, right = numsSize - 1;
int middle;
// 用的左闭右闭[left, right]
while (left <= right) {
middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
// 注意这里
right = middle - 1;
}else if (nums[middle] < target) {
left = middle + 1;
}else {
return middle;
}
}
return -1;
}
- 左闭右开
int search(int* nums, int numsSize, int target){
int left = 0, right = numsSize; //注意这里没有 减一
int middle = 0;
// 左闭右开 [left, right)
while (left < right) {
middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
// 注意这里
right = middle;
}else if (nums[middle] < target) {
left = middle + 1;
}else {
return middle;
}
}
return -1;
}
35、搜索插入位置

- 暴力解法
int searchInsert(int* nums, int numsSize, int target){
// 暴力解法
for (int i = 0; i < numsSize; i++) {
if (nums[i] >= target) {
return i;
}
}
return numsSize;
}
- 二分法:左闭右闭
int searchInsert(int* nums, int numsSize, int target){
// 二分法
int left = 0, right = numsSize - 1;
int middle = 0;
// 左闭右闭 [left, right]
while (left <= right) {
middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle - 1;
}else if (nums[middle] < target) {
left = middle + 1;
}else {
return middle;
}
}
// 注意这里,如果target没在数组里面,是返回的right + 1
return right + 1;
}
注意:这里返回 left 也是可以的
- 二分法:左闭右开
int searchInsert(int* nums, int numsSize, int target){
// 二分法
int left = 0, right = numsSize; // 注意这里没有减一
int middle = 0;
// 左闭右开
while (left < right) {
middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle;
}else if (nums[middle] < target) {
left = middle + 1;
}else {
return middle;
}
}
// 注意这里返回的是 right
return right;
}
注意:这里返回 left 也是可以的
34、在排序数组中查找元素的第一个和最后一个位置
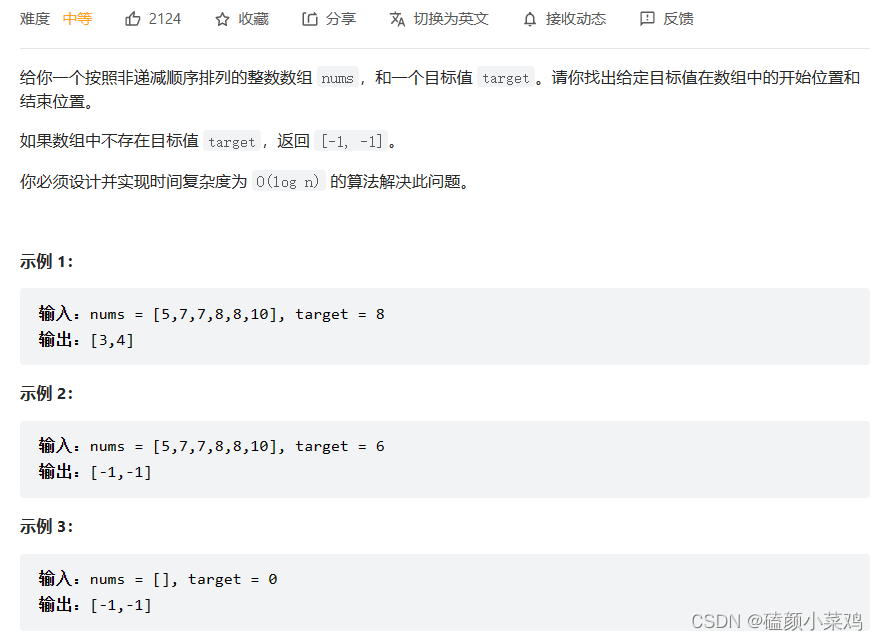
- 暴力求解
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* searchRange(int* nums, int numsSize, int target, int* returnSize){
int i;
int flag = 1;
int *ret = (int *)malloc(sizeof(int) * 2);
ret[0] = -1;
ret[1] = -1;
for (i = 0; i < numsSize; i++) {
if (nums[i] == target && flag == 1) {
ret[0] = i;
flag = 0;
}
if (nums[i] == target && flag == 0) {
ret[1] = i;
}
}
*returnSize = 2;
return ret;
}
- 二分法:分别找出左右边界
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int getRightBorder(int *nums, int numsSize, int target) {
int left = 0, right = numsSize - 1;
int middle = 0;
int rightBorder = -1;
while (left <= right) {
middle = left + ((right - left) >> 1);
if (nums[middle] == target) {
rightBorder = middle;
}
if (nums[middle] > target) {
right = middle - 1;
}else {
left = middle + 1;
}
}
return rightBorder;
}
int getLeftBorder(int *nums, int numsSize, int target) {
int left = 0, right = numsSize - 1;
int middle = 0;
int leftBorder = -1;
while (left <= right) {
middle = left + ((right - left) >> 1);
if (nums[middle] == target) {
leftBorder = middle;
}
if (nums[middle] < target) {
left = middle + 1;
}else {
right = middle - 1;
}
}
return leftBorder;
}
int* searchRange(int* nums, int numsSize, int target, int* returnSize){
int *ret = (int *)malloc(sizeof(int) * 2);
int rightBorder = getRightBorder(nums, numsSize, target);
int leftBorder = getLeftBorder(nums, numsSize, target);
if (rightBorder == -1 || leftBorder == -1) {
ret[0] = -1;
ret[1] = -1;
}else {
ret[0] = leftBorder;
ret[1] = rightBorder;
}
*returnSize = 2;
return ret;
}
69、x的平方根
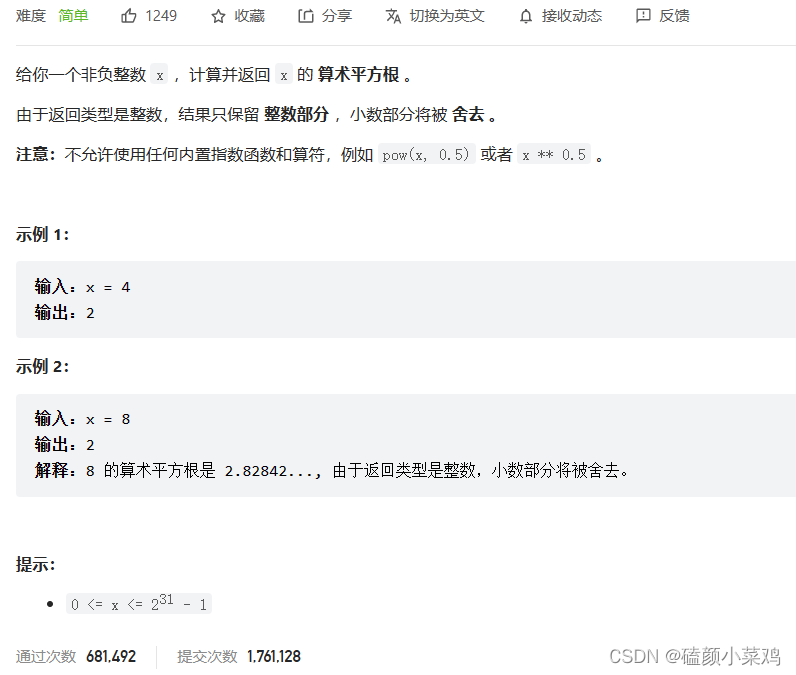
- 暴力求解
int mySqrt(int x){
// 暴力求解
int factor = 0;
for (int i = 0; i <= x; i++) {
if ((double)i * i <= x) {
factor = i;
}else {
return factor;
}
}
return x;
}
- 二分法
int mySqrt(int x){
int left = 0, right = x;
int middle = 0;
long temp = 0;
int factor = 0;
while (left <= right) {
middle = left + ((right - left) >> 1);
temp = (long)middle *middle;
if (temp <= x) {
factor = middle;
left = middle + 1;
}else {
right = middle -1;
}
}
return factor;
}
367、有效的完全平方数
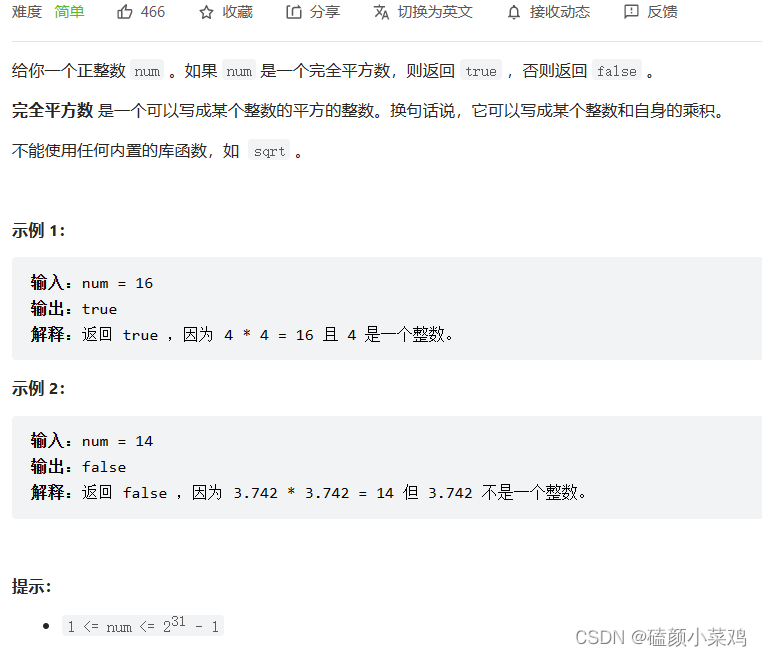
- 暴力求解
bool isPerfectSquare(int num){
// 暴力解法
int i;
for (i = 1; i <= (num / 2 + 1); i++) {
if ((long)i * i == num) {
return true;
}
}
return false;
}
- 二分法
bool isPerfectSquare(int num){
// 二分法
int left = 0, right = num;
int middle = 0;
while (left <= right) {
middle = left + ((right - left) >> 1);
if ((long)middle * middle == num) {
return true;
}else if ((long)middle * middle > num){
right = middle - 1;
}else {
left = middle + 1;
}
}
return false;
}
参考:《代码随想录》数组篇