1.快速排序

双边指针（交换法）：记录分界值，创建左右指针（记录下标）。

以第一个元素为分界值，先从右向左找出比分界值小的数据，然后从左向右找出比分界值大的数据；

左右指针下标未过界，交换左右指针数据；

循环查找交换，直到左右指针下标重合（这时右边都是比重合处大的数据，左边除了分界值都是比重合处小的数据），重合后交换分界值和重合下标数据，重合下标变为新分界值，再分别递归处理新分界值左右部分数据。

public void quickSort(int[] arr, int startIndex, int endIndex) {
    if (startIndex >= endIndex) {
        return;
    }
    // 找到分界值
    int pivotIndex = doublePointerSwap(arr, startIndex, endIndex);
    // 用分界值下标区分出左右区间，进行递归调用
    quickSort(arr, startIndex, pivotIndex - 1);
    quickSort(arr, pivotIndex + 1, endIndex);
}

private int doublePointerSwap(int[] arr, int startIndex, int endIndex) {
    int pivot = arr[startIndex];
    int leftPoint = startIndex;
    int rightPoint = endIndex;

    while (leftPoint < rightPoint) {
        // 从右向左找出比pivot小的数据
        while (leftPoint < rightPoint
                && arr[rightPoint] > pivot) {
            rightPoint--;
        }
        // 从左向右找出比pivot大的数据
        while (leftPoint < rightPoint
                && arr[leftPoint] <= pivot) {
            leftPoint++;
        }
        // 没有过界则交换
        if (leftPoint < rightPoint) {
            int temp = arr[leftPoint];
            arr[leftPoint] = arr[rightPoint];
            arr[rightPoint] = temp;
        }
    }
    // 最终将分界值与当前指针数据交换
    arr[startIndex] = arr[rightPoint];
    arr[rightPoint] = pivot;
    // 返回分界值所在下标
    return rightPoint;
}

2.归并排序

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

public int[] mergeSort(int[] nums, int low, int high) {
    if (low == high) return new int[] { nums[low] };

    int mid = (low + high)/ 2;
    int[] leftArr = mergeSort(nums, low, mid); //左有序数组
    int[] rightArr = mergeSort(nums, mid + 1, high); //右有序数组
    int[] newNum = new int[leftArr.length + rightArr.length]; //新有序数组

    int m = 0, i = 0, j = 0;
    while (i < leftArr.length && j < rightArr.length) {
        newNum[m++] = leftArr[i] <= rightArr[j] ? leftArr[i++] : rightArr[j++];
    }
    while (i < leftArr.length)
        newNum[m++] = leftArr[i++];
    while (j < rightArr.length)
        newNum[m++] = rightArr[j++];
    return newNum;
}

3.比较

归并排序的比较次数小于快速排序的比较次数；移动（赋值）次数一般多于快速排序的移动次数。

归并排序的内存占用高于快速排序，快速排序时原地排序，空间复杂度为O(1)，归并排序不是原地排序，数组合并需要额外空间。

快速排序是边分解边排序，每次分解都实现整体上有序，即参照数左侧的数小于参照值，右侧的大于参照值；归并排序是先递归分解到最小区间，然后从小区间开始合并排序，是自下而上的排序。

快速排序是不稳定的，时间复杂度在O(nlogn)~O(n^2)之间，归并排序是稳定的，时间复杂度是O(nlogn)。

哪个更快？

C++毫无疑问是快速排序（C++有很强的inline优化机制，比较操作比赋值操作要快的多）。

Java有点复杂，基本数据类型如(int/double)，快排更快；复杂数据类型（对象）则不一定，有可能归并排序快，也有可能快排快，取决于比较和赋值操作哪个更快。

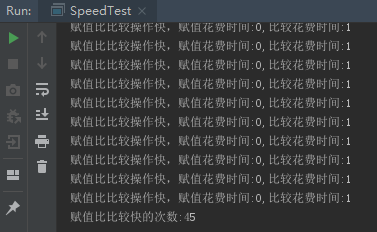
下面代码就可以测试出部分情况赋值操作比较比较操作更快。

    public static void main(String[] args) {
        int assignmentFast = 0;
        for(int k=0; k<100; k++){
            int len = 1024 * 1024 ;
            NumTest[] numArray = new NumTest[len];
            for(int i=0; i<numArray.length; i++){
                NumTest numTest = new NumTest();
                numTest.setNum1(RandomUtil.getNum(1,9999));
                numTest.setNum2(RandomUtil.getNum(1,9999));
                numArray[i] = numTest;
            }
            long startTime = System.currentTimeMillis();
            for(int i=0; i<numArray.length; i++){
                if(numArray[0].compareTo(numArray[i]) > 0){}
            }
            long compareSpend = System.currentTimeMillis()-startTime;

            startTime = System.currentTimeMillis();
            for(int i=0; i<numArray.length; i++){
                numArray[0] = numArray[i];
            }
            long moveSpend = System.currentTimeMillis()-startTime;
            if(moveSpend < compareSpend){
                assignmentFast++;
                System.out.println("赋值比比较操作快，赋值花费时间:"+moveSpend+",比较花费时间:"+compareSpend);
            }
        }
        System.out.println("赋值比比较快的次数:"+ assignmentFast);
    }

    static class NumTest implements Comparable<NumTest>{
        int num1;
        int num2;

        public int getNum1() {
            return num1;
        }

        public void setNum1(int num1) {
            this.num1 = num1;
        }

        public int getNum2() {
            return num2;
        }

        public void setNum2(int num2) {
            this.num2 = num2;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            NumTest numTest = (NumTest) o;
            return num1 == numTest.num1 &&
                    num2 == numTest.num2;
        }

        @Override
        public int hashCode() {
            return Objects.hash(num1, num2);
        }

        @Override
        public int compareTo(NumTest o) {
            int otherSum = o.getNum1() + o.getNum2();
            int localSum = num1 + num2;
            if(localSum == otherSum){
                return 0;
            }
            return localSum>otherSum?1:-1;
        }
    }