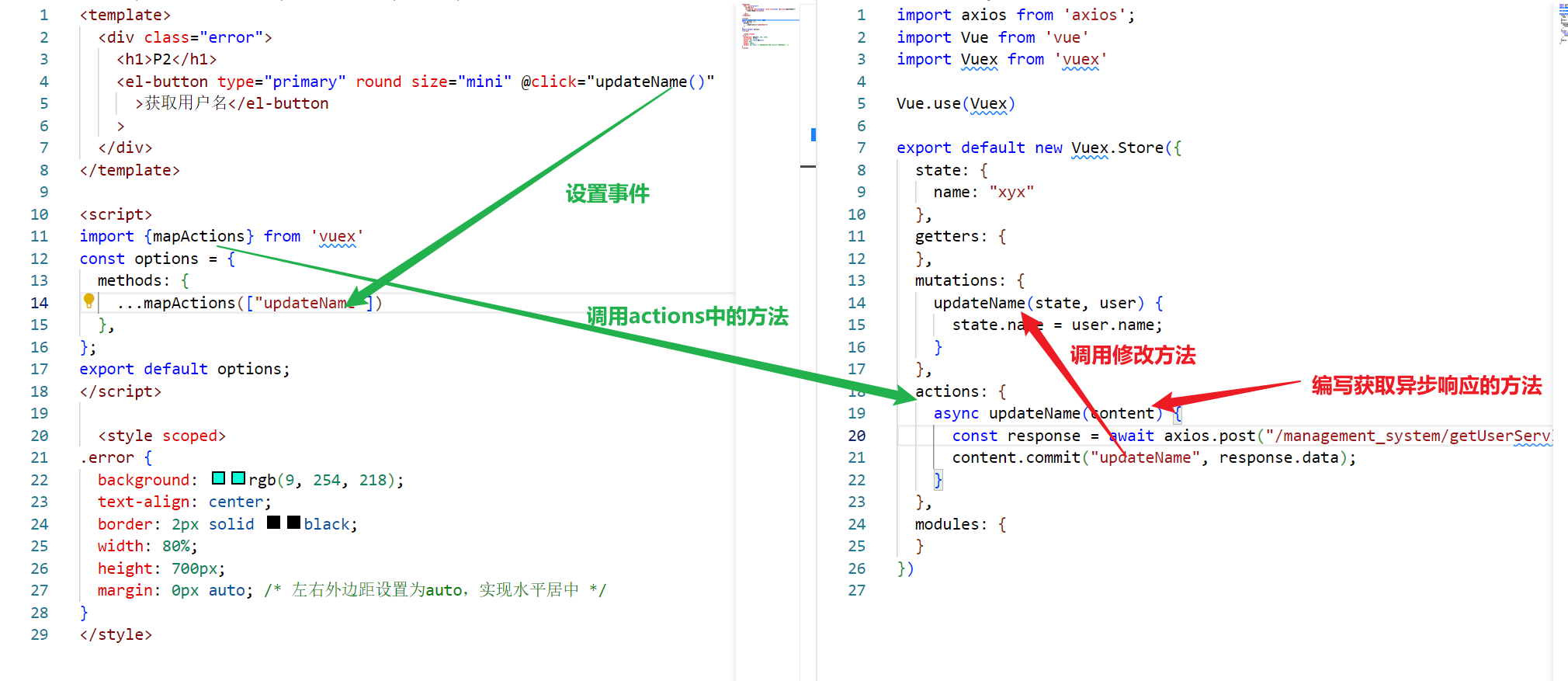
题目

思路

多次修改操作，为降低复杂度，采用差分。

差分数组的性质可以转化这个“所有数都一样”的目标，转化为”b[2] ~ b[n] 均为0“的目标。

为了使得方法数最少，要使得方法中不存在前后矛盾的部分，比如减了又加。

（另外注意，差分中b[l] 和 b[r+1]的修改方法决定了l 不等于 r +1，不然r < l ）

于是，我们考虑对于b[i]的正元素和负元素，我们需要找b[1]或者b[n+1]这两个合法的对象来形成

（b[1] += c, b[i] -= c）或者 （b[i] += c，b[n+1] -= c）以及其他的普通处理对。

令pos为所有正元素之和，neg为所有负元素的绝对值之和（下标2~n）

组成操作数的第一个部分就是正元素 -= 1, 负元素 += 1的操作数（普通处理对）。        min(pos, neg)

第二个部分就是全正或者全负的处理（处理对没限定）。        abs(pos - neg)

总操作数 min(pos, neg) + abs(pos - neg)

（上面第二个部分没考虑用哪个处理对，下面要考虑了）

“不同结果的数目”，也就是b[1]的可能取值数，需要利用（b[1] += c，b[i] -= c）的处理对来考虑，b[1]的增长需要在b[i] > 0，c = 1条件下。b[1]的max为b[1] + pos。同理，min为b[1] - neg。加上b[1]自身

一共pos+neg+1。? 错了！没有保证操作数最小。

操作数最小建立在“组成操作数的一部分就是正元素 -= 1, 负元素 += 1的操作数”的基础上，所以

第一个部分不会用特殊处理对（b[1] += c，b[i] -= c），只有第二个部分才可以用，这部分的数目为abs(pos-neg)，所以b[1]的单向偏移量也就是这么多，加上自身，

是abs(pos - neg) + 1

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
long long a[N];
long long b[N];
void insert(int l, int r, int c)
{
    b[l] += c;
    b[r+1] -= c;
}
int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        insert(i, i, a[i]);
    }
    long long pos = 0, neg = 0;
    for(int i = 2; i <= n; i++)
    {
        (b[i] > 0) ? pos += b[i] : neg -= b[i];
    }
    
    cout << min(pos, neg) + abs(pos - neg) << endl;
    cout << abs(pos - neg) + 1 << endl;
    
    return 0;
}