信息学奥赛初赛天天练-54-CSP-J2019阅读程序3-二叉树、满二叉树、单侧二叉树、二分查找、递归、等差数列求和

news2024/9/19 9:54:28

PDF文档公众号回复关键字:20240803

在这里插入图片描述

2019 CSP-J 阅读程序3

1阅读程序(程序输入不超过数组或字符串定义的范围；判断题正确填 √，错误填 ×。除特殊说明外，判断题 1.5 分，选择题 3 分，共计 40 分)

01 #include <iostream>
02 using namespace std;
03 const int maxn = 10000;
04 int n;
05 int a[maxn];
06 int b[maxn];
07 int f(int l, int r, int depth) {
08     if (l > r)
09         return 0;
10    int min = maxn, mink;
11    for (int i = l; i <= r; ++i) {
12         if (min > a[i]) {
13             min = a[i];
14             mink = i;
15         }
16     }
17     int lres = f(l, mink - 1, depth + 1);
18     int rres = f(mink + 1, r, depth + 1);
19     return lres + rres + depth * b[mink];
20 }
21 int main() {
22     cin >> n;
23     for (int i = 0; i < n; ++i)
24         cin >> a[i];
25     for (int i = 0; i < n; ++i)
26         cin >> b[i];
27     cout << f(0, n - 1, 1) << endl;
28     return 0;
29 }

1 如果a数组有重复的数字，则程序运行时会发生错误。( )[1.5分]

2 如果b数组全为0,则输出为0。( ) [1.5分]

3 当n=100时，最坏情况下，与第12行的比较运算执行的次数最接近的是：( ) [3分]

A 5000

B 600

C 6

D 100

4 当n=100时，最好情况下，与第12行的比较运算执行的次数最接近的是：( ) [3分]

A 100

B 6

C 5000

D 600

5 当n=10时，若b数组满足，对任意0<=i<n,都有b[i］ = i + 1,那么输出最大为( ) [3分]

A 386

B 383

C 384

D 385

6 当n=100时，若b数组满足，对任意0 <= i < n,都有b[i］=1,那么输出最小为( ) [4分]

A 582

B 580

C 579

D 581

2 相关知识点

1) 二叉树

每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点)，并且，二叉树的子树有左右之分，其次序不能任意颠倒，例如下面是一棵二叉树

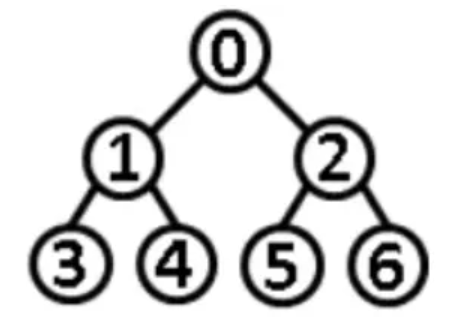
满二叉树

满二叉树又叫完美二叉树，除了叶子结点之外的每一个结点都有两个孩子，树的叶子节点均在最后一层（也就是形成了一个完美的三角形）

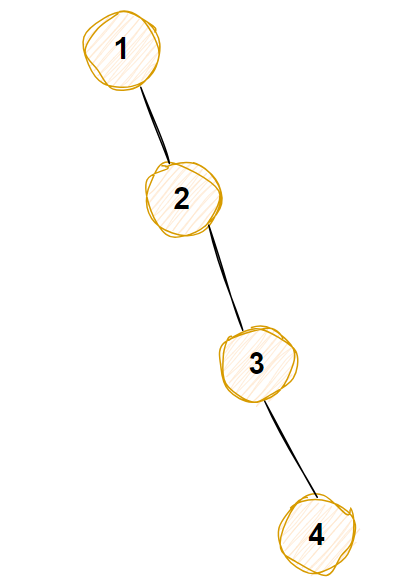
单侧二叉树

每1层只有左孩子或者右孩子的二叉树

2) 二分查找

二分查找也叫二分搜索 (binary search)，也叫折半查找 (half-interval search)，是一种在有序数组中查找特定元素的搜索算法。

所以用二分查找的前提是数组必须是有序的，可以升序也可以降序

平均时间复杂度

O(logn)

3) 递归

递归

递归是一种解决问题的方法，它通过将问题分解为更小的子问题来解决。

一个递归函数会在其定义中直接或间接地调用自身

递归通常包括两个部分：基本情况（Base case）和递归步骤（Recursive step）。

基本情况是指当问题规模变得足够小时，可以直接得到解决方案的情况。

4) 等差数列求和

等差数列求和公式

sn=(a1+an)*n/2

其中a1是第1项，an是第n项，n是总共n个数求和
例如

1+2+3+4+5+6=(1+6)*6/2=21
2+4+6+8+10=(2+10)*5/2=30

3 思路分析

大致思路

每1层找到1个最小值，把剩余数分成左右2部分(如果找到的是最小或最大，剩余的只能分成1部分)

拆分后的每部分再继续找到最小值，继续拆分

递归下去，直到最后1层，每个元素都有1个数，不能再拆分为止

示例

a和b数组

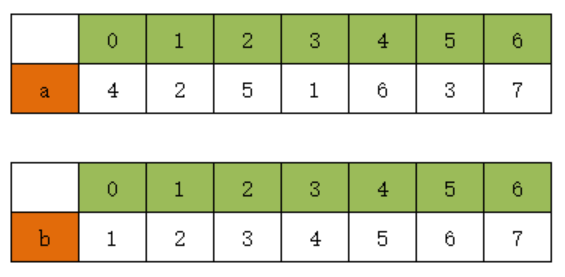
对应拆分如下

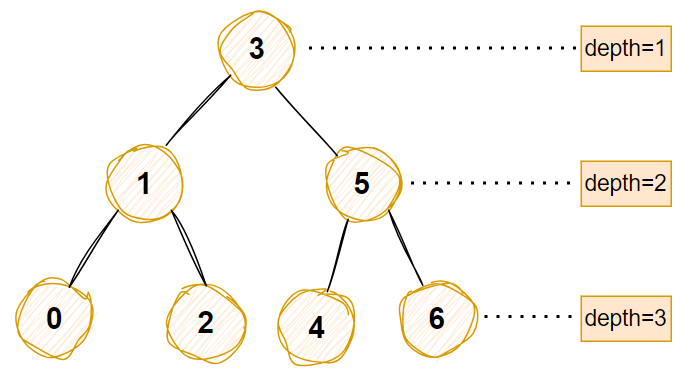
计算输出

ans=b[3]*1 +b[1]*2+b[5]*2+b[0]*3+b[2]*3+b[4]*3+b[6]*3
   =4*1    + 2*2  + 6*2  + 1*3  +3*3   + 5*3  +7*3
   =4      + 4    + 12   +  3   +9     +15    +21
   =68

1 如果a数组有重复的数字，则程序运行时会发生错误。( F )[1.5分]

分析

如下程序，通过循环比较求最小数及其下标，每次可以找到第1个最小数，不会发生错误
11    for (int i = l; i <= r; ++i) {
12         if (min > a[i]) {
13             min = a[i];
14             mink = i;
15         }
16     }

2 如果b数组全为0,则输出为0。( T ) [1.5分]

分析

由如下程序可知，返回值是下一层左边返回值+下一层右边返回值+当前层*最小值对应b数组的值
如果考虑到最后一层，左右返回值都是0，所以函数返回值取决于b数组的值
如果b数组全是0，depth*b[mink]也全是0，因此输出0
17     int lres = f(l, mink - 1, depth + 1);
18     int rres = f(mink + 1, r, depth + 1);
19     return lres + rres + depth * b[mink];

3 当n=100时，最坏情况下，与第12行的比较运算执行的次数最接近的是：( A ) [3分]