单调栈
- 单调栈的概述(Overview)
- 何时使用单调栈
- 模拟单调递增栈
- 单调栈的运用(算法练习题)
- 模板
- 【练习一、单调栈】739. 每日温度
- 【练习二、单调栈+哈希表】496. 下一个更大元素 I
- 【练习三、单调栈+循环数组】503. 下一个更大元素 II
- 【练习四、单调栈】👍42.接雨水
- 【练习五、单调栈】👍84. 柱状图中最大的矩形
单调栈我是跟着代码随想录刷题的时候看见的,觉得挺有趣的、也挺好用的,然后就来CSDN找博客学习了。代码随想录是用C++去解决算法问题,我也喜欢用C++去刷题,这里题解等用的是Java。借用了这篇《单调栈》博客以及代码随想录推荐的题!!!
单调栈的概述(Overview)
单调栈是指栈内元素是单调的,固分为单调递增栈/单调递减栈。
- 单调递增栈:栈内元素递增,是由低向顶的。
- 单调递减栈:与上相反。
何时使用单调栈
通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
模拟单调递增栈
单调栈内部是一般情况放索引的,结合实际的一维数组,对右边或左边首个大或小的元素的索引进行保存和分析。
现在有一组数10,3,7,4,12。从左到右依次入栈,则如果栈为空或入栈元素值小于栈顶元素值,则入栈;否则,如果入栈则会破坏栈的单调性,则需要把比入栈元素小的元素全部出栈。单调递减的栈反之。
-
10入栈时,栈为空,直接入栈,栈内元素为10。
-
3入栈时,栈顶元素10比3大,则入栈,栈内元素为10,3。
-
7入栈时,栈顶元素3比7小,则栈顶元素出栈,此时栈顶元素为10,比7大,则7入栈,栈内元素为10,7。
-
4入栈时,栈顶元素7比4大,则入栈,栈内元素为10,7,4。
-
12入栈时,栈顶元素4比12小,4出栈,此时栈顶元素为7,仍比12小,栈顶元素7继续出栈,此时栈顶元素为10,仍比12小,10出栈,此时栈为空,12入栈,栈内元素为12。
当然入栈的也可以是索引,然后取出索引结合一维数组再和实际元素比较。
单调栈的运用(算法练习题)
模板
假设一维数组是 nums,ans 数组对应索引的值为 下一个大或者小的数的索引。
Stack<Integer> stack = new Stack<>();
for(int i=0;i<nums.length;++i){
// 如果是找右边大于的一个数就是 < 号进行出栈,反之是大于进行出栈
// 下面是找右边大于的第一个数
while(!stack.empty() && nums[stack.peek()]<nums[i]){
ans[stack.peek()] = i;// 这里根据具体题目进行定义ans 数组,要长度就索引,要那个大的数的值就 nums[i] 值
stack.pop();
}
stack.push(i);
}
【练习一、单调栈】739. 每日温度
每日温度
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int[] ans = new int[temperatures.length];
Arrays.fill(ans,0);// 初始化
Stack<Integer> stack = new Stack<>();
for(int i=0;i<temperatures.length;++i){
while(!stack.empty() && temperatures[stack.peek()]<temperatures[i]){
ans[stack.peek()] = i - stack.peek();// 直接处理得出答案
stack.pop();
}
stack.push(i);
}
stack.clear();
return ans;
}
}
【练习二、单调栈+哈希表】496. 下一个更大元素 I
下一个更大元素 I
class Solution {
private Map<Integer,Integer> map = new HashMap<>();
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
init(nums2);
int[] temp = new int[nums2.length];// 存nums2 中每个数的右边更大的元素
Arrays.fill(temp,-1);// 初始化
Stack<Integer> stack = new Stack<>();
for(int i=0;i<nums2.length;++i){
while(!stack.empty() && nums2[stack.peek()]<nums2[i]){
temp[stack.peek()] = nums2[i];
stack.pop();
}
stack.push(i);
}
int[] ans = new int[nums1.length];
for(int i=0;i<nums1.length;++i){
ans[i] = temp[map.get(nums1[i])];
}
return ans;
}
/**
这是对map 集合进行初始化,把nums2 数组中数的索引记录下来
*/
private void init(int[] nums){
for(int i=0;i<nums.length;++i)
map.put(nums[i],i);
}
}
【练习三、单调栈+循环数组】503. 下一个更大元素 II
下一个更大元素 II
class Solution {
public int[] nextGreaterElements(int[] nums) {
int len = nums.length*2;// 循环数组
Deque<Integer> stack = new ArrayDeque<>();// 单调递增栈,存放索引
int[] ans = new int[nums.length];
Arrays.fill(ans,-1);// 初始化
for(int i=0;i<len;++i){
while(!stack.isEmpty() && nums[stack.peek()]<nums[i%nums.length]){
ans[stack.peek()] = nums[i%nums.length];
stack.pop();
}
stack.push(i%nums.length);
}
return ans;
}
}
【练习四、单调栈】👍42.接雨水
接雨水
听说这是高频面试题;
解题的方法不唯一(这里使用的是单调栈的解法):
- 双指针
- 动态规划
- 单调栈
解这题是思路就两种,按行求雨水,按列求雨水。
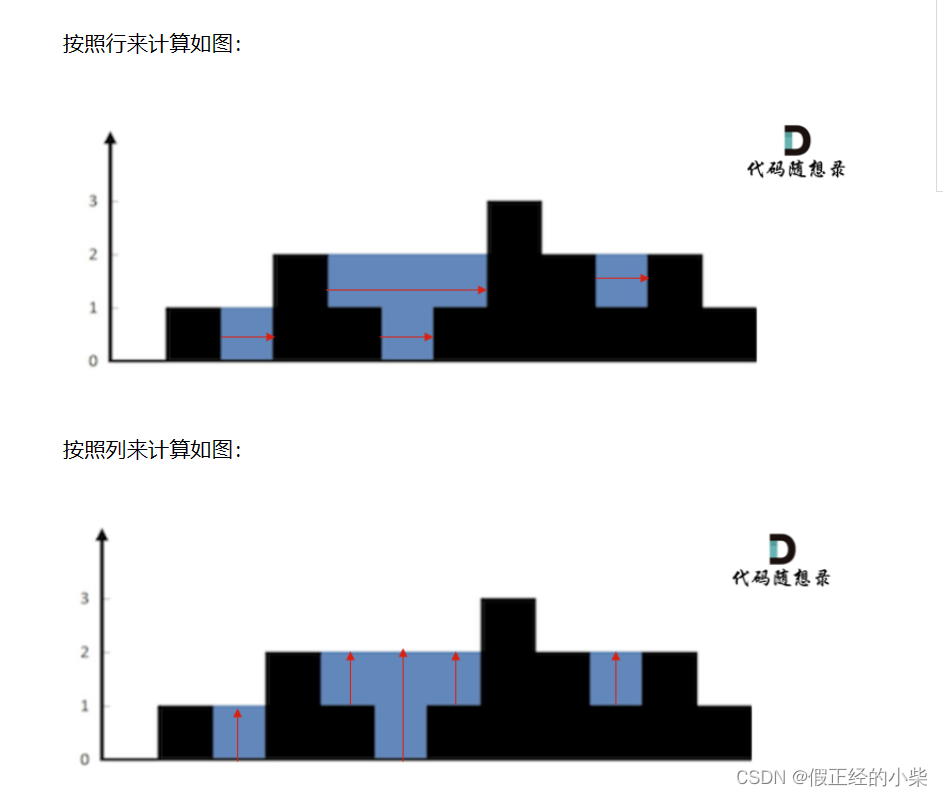
使用单调栈来解这题是使用行来计算的。
class Solution {
public int trap(int[] height) {
Deque<Integer> stack = new ArrayDeque<>();// 存放索引,单调递增栈
int sum = 0;
for(int i=0;i<height.length;++i){
while(!stack.isEmpty() && height[stack.peek()]<height[i]){
// 产生凹型的时候才会接住雨水
// 这是凹形中间柱
int midH = height[stack.peek()];
stack.pop();
// 获取产生高度差的最低柱子
if(!stack.isEmpty()){
int minH = Math.min(height[i],height[stack.peek()]);
int len = i - stack.peek() - 1;
sum += (minH-midH)*len;
}
}
stack.push(i);
}
return sum;
}
}
【练习五、单调栈】👍84. 柱状图中最大的矩形
柱状图中最大的矩形
这题把我头给整大了。和上面一题有类似的地方,但不多。
动态规划解决这题可能更好写些。单调栈解决这题,需要创建新数组,在原数组的首尾加上0,想到这里了就见到了,单调栈中仍存放索引,对应的数是单调递增的,然后遇到小于它的数,可以对左右边界然后计算其最大面积然后与ans进行比较。
class Solution {
public int largestRectangleArea(int[] heights) {
int len = heights.length;
List<Integer> newH = new ArrayList<>();
newH.add(0);
for(int h:heights){
newH.add(h);
}
newH.add(0);
// 制作新的数组,在原来基础上,左右加个0高度柱子
// 最左边的0是为了第一个小数
// 最右边的是为了情况单调栈
Deque<Integer> stack = new ArrayDeque<>();// 存放左边第一个小的数的索引,单调递增栈
int ans = 0;
for(int i=0;i<newH.size();++i){
while(!stack.isEmpty() && newH.get(stack.peek())>newH.get(i)){
int mid = stack.peek();
stack.pop();
int left = stack.peek();// 左边最小索引
int right = i;// 右边最小索引
ans = Math.max((right-left-1)*newH.get(mid),ans);
}
stack.push(i);
}
return ans;
}
}