目录

动态规划问题

一:01背包问题

1.问题描述

2.分析问题

3.代码实现(二维数组)

4.滚动数组实现(一维数组)

二:完全背包问题

1.题目描述

2.问题分析

3.代码实现

---

动态规划问题

动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题,进行解决，从而一步步获取最优解的处理算法

动态规划对于解决最优子结构啊和重叠子问题等问题时候,有着很好的应用

对于动态规划问题,大致可以分为以下几步:

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

一:01背包问题

1.问题描述

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

例如以下问题:

有一个背包,它的容量为4磅,现有以下物体

物品	重量	价格
物品0	1	1500
物品1	4	3000
物品2	3	2000

1)要求达到的目标为装入的背包的总价值最大，并且重量不超出                                                    2)要求装入的物品不能重复

2.分析问题

对于解决这样的动态规划的背包问题,还是采用通用的五个步骤

1.确定dp数组（dp table）以及下标的含义

对于01背包问题,可以采用二维数组或者一维数组,这里为了便于理解,先采用一维数组

定义一个二维数组dp[i][j],这里dp数组的含义为:将物品(0到i)放入到背包容量为j的背包里面,价值总和最大为dp[i][j]

2.确定递推公式

对于放入物品i,有两种状态:将物品i放入到背包中,不将物品i放入到背包中

不放物品i:不放物品i,相当于将物品0到i-1放入到背包容量为j的背包中,这个时候递推公式dp[i][j]就可以等于dp[i-1][j]

放物品i:当放入物品i的时候,此时首先需要判断的是否物品i可以放入到背包容量为j的背包中,要是使背包可以放入物品i,则背包的容量至少剩余weight[i],即放入物品0到i-1的时候,背包剩余的容量至少为j-weight[i],因此放入0到i-1物品的最大价值为dp[i-1][j-weight[i]],放入物品i时候的最大价值就为dp[i-1][j-weight[i]]+value[i]

此时dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])

3.dp数组如何初始化

由递推公式dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])可以看出,第i行需要由上一行推算出,所以第i=0行的数据一定要进行初始化,具体如下

        for (int i = weight[0]; i <= bagSize; ++i) {
            dp[0][i] = value[0];
        }

4.确定遍历顺序

实现先遍历背包还是先遍历物品,其实都可以,但是先遍历物品更好理解

确定递推的方向:

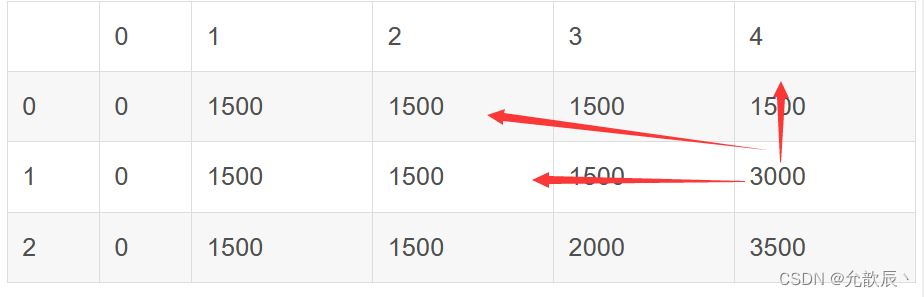
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的,dp[i][j]是由其左上角的元素推出来的,因此需要自上到下,自左到右的遍历顺序

5.举例推导dp数组

对dp数组进行填表的操作

	0	1	2	3	4
0	0	1500	1500	1500	1500
1	0	1500	1500	1500	3000
2	0	1500	1500	2000	3500

3.代码实现(二维数组)

    public static int maxValue(int[] weight, int[] value, int bagSize) {
        int num = weight.length;
        int[][] dp = new int[num][bagSize + 1];//0-i物品任取到容量为j的背包的最大价值
        for (int i = weight[0]; i <= bagSize; ++i) {
            dp[0][i] = value[0];
        }
        for (int i = 1; i < num; ++i) {
            for (int j = 1; j <= bagSize; ++j) {
                if (j < weight[i]) {//如果当前物品的重量大于背包的容量
                    dp[i][j] = dp[i - 1][j];//不取当前的物品
                } else {
                    //dp[i - 1][j]不取当前的物品的价值,
                    //dp[i - 1][j - weight[i]] + value[i]取当前物品
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
                }

            }
        }
        return dp[num - 1][bagSize];

    }

4.滚动数组实现(一维数组)

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

下一行的元素仅有上一行的元素推出来,因此可以使用滚动数组,也就是一维dp数组

1.确定dp数组（dp table）以及下标的含义

dp[j]表示背包容量为j的商品最大价值为dp[j]

2.确定递推公式

和二维dp数组一样,也是有两种选择,一种放入物品i,一种不放物品i,因此可以写成

此时dp[j]=max(dp[j],dp[j-weight[i]]+value[i])

3.dp数组如何初始化

根据递推公式可以看出dp[j]由此层推出,此时我们可以将dp初始化为0

4.确定遍历顺序

上面我们已经写过了二维dp数组,我们知道本层是由下上方的元素推出来的,现在我们采用的是一维dp数组,如果我们还是采用从左到右进行递推的话,后面的元素就可能因为前边元素的变化而变化,不是由上一层的元素推出来的了,相当于二维dp数组我们根据本层前边的元素推出本层后边的元素,这样就不符合我们想要表达的意思了,如何我们采用的是从右到左的遍历顺序的话,这样彼此之间就不会因为后边元素的改变而影响前边元素的改变了,相当于上一层的元素推出本层的元素

这里是与二维dp数组最大的不同,需要自己理解清楚

5.举例推导dp数组

三次for循环的数据如下

第一次
0	1500	1500	1500	1500
第二次
0	1500	1500	1500	3000
第三次
0	1500	1500	2000	3500

 代码实现

    public static int maxValue(int[] weight, int[] value, int bagSize) {
        int[] dp = new int[bagSize + 1];//0-i物品任取到容量为j的背包的最大价值

        for (int i = 0; i < weight.length; ++i) {//物品的数量
            for (int j = bagSize; j >= weight[i]; --j) {//背包剩余的重量
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
            System.out.println(Arrays.toString(dp));

        }
        return dp[bagSize];

    }

二:完全背包问题

1.题目描述

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

例如如下问题:

有一个背包,它的容量为4磅,现有以下物体

物品	重量	价格
物品0	1	1500
物品1	4	3000
物品2	3	2000

完全背包问题与01背包问题基本相似,唯一的区别就是多重背包问题的物品数量是无限的

2.问题分析

01背包的滚动数组的遍历顺序是从右到左的,可以保证每个物品只被遍历一次,而完全背包问题每个物品可以被添加多次,因此需要进行从左到右进行遍历,可以确保每个物品有被多次添加的可能

举例推导dp数组

第一次
0	1500	3000	4500	6000
第二次
0	1500	3000	4500	6000
第三次
0	1500	3000	4500	6000

3.代码实现

    public static int perfectPackage(int[] weight, int[] value, int bagWeight) {
        int[] dp = new int[bagWeight + 1];
        for (int i = 0; i < weight.length; ++i) {
            for (int j = weight[i]; j <= bagWeight; ++j) {
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        return dp[bagWeight];

    }