代码随想录算法训练营第十七天 | 110.平衡二叉树，257. 二叉树的所有路径，404.左叶子之和

news2024/9/20 16:56:38

一、昨日回顾与补充

今天看了Day16讲解的视频，对于求二叉树最大深度、最小深度以及求完全二叉树的节点个数有了新的理解，总结如下：

1.深度和高度的区别（之前就看看定义忽略了）

  • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。

  • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

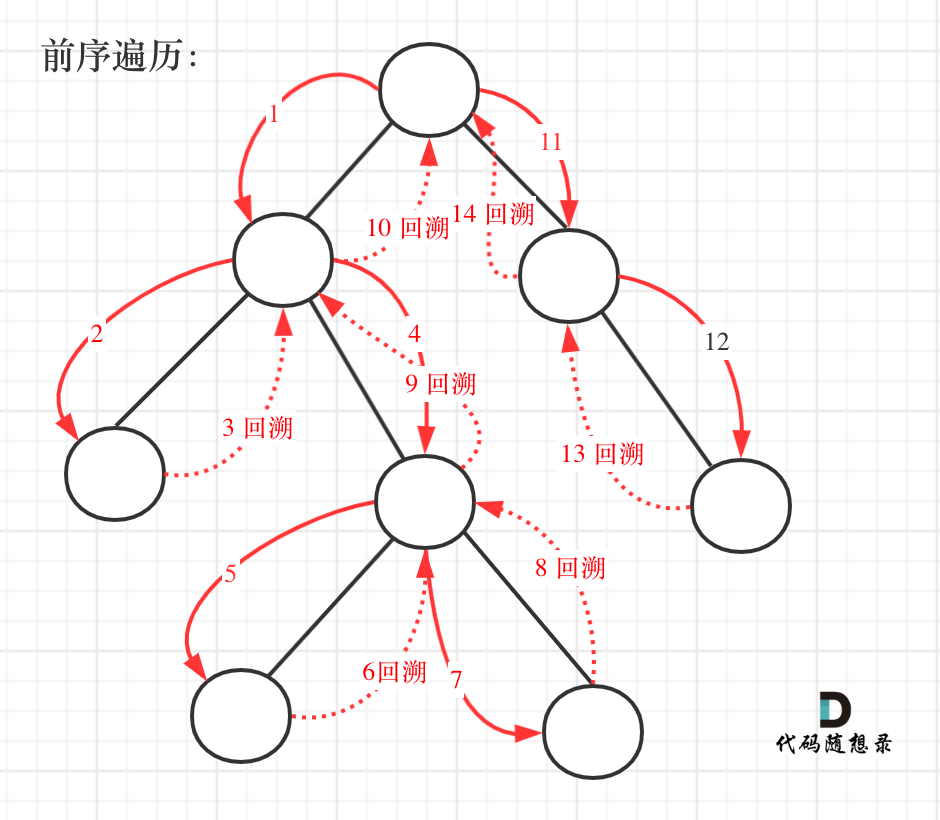
在递归遍历的过程中，按照正常逻辑来说应该是前序遍历（中左右）自上而下求深度，但是这样写的代码比较麻烦，因此大多采用后序（左右中）自下而上的写法将求深度间接转化为求高度的过程。具体如下：

  • 求二叉树的最大深度即求根节点到最远叶子节点的高度。

根节点的高度就是二叉树的最大深度，所以本题中可以通过后序求的根节点高度来求的二叉树最大深度。

  • 求二叉树的最小深度即求根节点到最近左右子树都为空的叶子节点的高度。

使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。

2. LeetCode104 二叉树的最大深度 LeetCode111 二叉树的最小深度
// 最大深度——简化版
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
};

// 具体后序遍历实现逻辑
class Solution {
public:
    // 通过后序遍历求根节点到叶子结点的最大高度 = 二叉树的最大深度
    int getHeight(TreeNode* node) {
        if (node == NULL) return 0;
        int leftHeight = getHeight(node->left);    // 左
        int rightHeight = getHeight(node->right);  // 右
        int res = 1 + max(leftHeight, rightHeight);// 中
        return res;
    }
    int maxDepth(TreeNode* root) {
        return getHeight(root);
    }
};
// 最小深度——简化版
class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right != NULL) {
            return 1 + minDepth(root->right);
        }
        if (root->left != NULL && root->right == NULL) {
            return 1 + minDepth(root->left);
        }
        return 1 + min(minDepth(root->left), minDepth(root->right));
    }
};

// 具体后序遍历实现逻辑
class Solution {
public:
    int getHeight(TreeNode* node) {
        if (node == NULL) return 0;
       
        int leftHeight = getHeight(node->left);    // 左
        int rightHeight = getHeight(node->right);  // 右
        // 中
        if (node->left == NULL && node->right != NULL) {
            return 1 + rightHeight;
        }
        if (node->left != NULL && node->right == NULL) {
            return 1 + leftHeight;
        }
        return 1 + min(leftHeight, rightHeight);
    }
    int minDepth(TreeNode* root) {
        return getHeight(root);
    }
};
3. 完全二叉树的解法

方法一，当做普通二叉树（迭代法和递归法）——迭代法采用队列的方式实现，递归法采用后序遍历的方式，简化版真的很简单。

方法二，充分利用完全二叉树的特点来做。在递归的思路中，对某节点将定义两个指针left和right，分别指向左右孩子，利用while循环遍历左子树的节点深度和右子树的深度。如果得到的遍历结果是相等的，那么证明以当前节点为根节点的子树是一颗满二叉树（它是完全二叉树的子集），因此可以利用满二叉树的公式求节点个数（即2^深度-1），具体代码实现可以采用位运算，这样在树比较大时能节省很多时间。

// 方法一：当做普通二叉树来求节点个数的简化版代码
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == NULL) return 0;
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};

// 具体逻辑实现（后序遍历）
class Solution {
public:
    int getNodesSum(TreeNode* cur) {
        if (cur == NULL) return 0;
        int leftNum = getNodesSum(cur->left);    // 左
        int rightNum = getNodesSum(cur->right);  // 右
        int treeNum = leftNum + rightNum + 1;    // 中
        return treeNum;
    }
    int countNodes(TreeNode* root) {
        return getNodesSum(root);
    }
};

// 当做普通二叉树的迭代法实现代码——即层序遍历的模板
class Solution {
public:
    int countNodes(TreeNode* root) {
        queue<TreeNode*> que;
        int result = 0;
        if (root != NULL) que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                result++;
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return result;
    }
};
// 方法二：利用完全二叉树的特征，递归版的简化版代码
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == NULL) return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftNums = 0, rightNums = 0;
        while (left) {
            left = left->left;
            leftNums ++;
        }
        while (right) {
            right = right->right;
            rightNums ++;
        }
        if (leftNums == rightNums) {
            return (2 << leftNums) - 1;
        }
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

// 具体逻辑实现
class Solution {
public:
    int getNums(TreeNode* node) {
        if (node == NULL) return 0;
        TreeNode* left = node->left;
        TreeNode* right = node->right;
        int leftNums = 0;
        int rightNums = 0;

        // 一直向左遍历左子树
        while (left) {
            left = left->left;
            leftNums++;
        }
        // 一直向右遍历右子树
        while (right) {
            right = right->right;
        }

        if (leftNums == rightNums) {
            // 左移 位运算
            return (2 << leftNums) - 1;
        }

        leftNums = getNums(node->left);
        rightNums = getNums(node->right);
        return 1 + leftNums + rightNums;
    }
    int countNodes(TreeNode* root) {
        return getNums(root);
    }
};

二、参考资料

平衡二叉树 （优先掌握递归）

题目链接/文章讲解/视频讲解：https://programmercarl.com/0110.%E5%B9%B3%E8%A1%A1%E4%BA%8C%E5%8F%89%E6%A0%91.html

二叉树的所有路径 （优先掌握递归）

题目链接/文章讲解/视频讲解：https://programmercarl.com/0257.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%89%80%E6%9C%89%E8%B7%AF%E5%BE%84.html

左叶子之和 （优先掌握递归）

题目链接/文章讲解/视频讲解：https://programmercarl.com/0404.%E5%B7%A6%E5%8F%B6%E5%AD%90%E4%B9%8B%E5%92%8C.html

三、LeetCode110.平衡二叉树

https://leetcode.cn/problems/balanced-binary-tree/description/

示例1：

示例2：

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树 每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：（如上图）
输入：root = [3,9,20,null,null,15,7] 输出：true
示例 2：（如上图）
输入：root = [1,2,2,3,3,null,null,4,4] 输出：false
示例 3：
输入：root = [] 输出：true
提示：
树中的节点数在范围 [0, 5000] 内
-10^4 <= Node.val <= 10^4 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 后序遍历（左右中）自下而上求高度，不适合采用前序，如果先判断中间节点，会出现由于其子树的高度未知无法进一步得到当前的子树是否是平衡二叉树
    int getHeight(TreeNode* node) {
        if (node == NULL) return 0;
        int leftHeight = getHeight(node->left);   // 左
        int rightHeight = getHeight(node->right); // 右
        if (leftHeight == -1) return -1;          
        if (rightHeight == -1) return -1;
        int res = -1;                             // 中
        if (abs(leftHeight - rightHeight) > 1) {
            res = -1;
        } else {
            res = 1 + max(leftHeight, rightHeight); // 父节点 + 其子树的高度
        }
        return res;
    }
    bool isBalanced(TreeNode* root) {
        int res = getHeight(root);
        if (res == -1) return false;
        return true;
    }
};
// 不断简化一
class Solution {
public:
    // int isbal = true;
    // 后序遍历（左右中）自下而上求高度，不适合采用前序，如果先判断中间节点，会出现由于其子树的高度未知无法进一步得到当前的子树是否是平衡二叉树
    int getHeight(TreeNode* node) {
        if (node == NULL) return 0;
        int leftHeight = getHeight(node->left);   // 左
        int rightHeight = getHeight(node->right); // 右
        // 剪枝 如果某节点的子树已经不是平衡二叉树，那么整棵树就不是平衡二叉树，不用再继续求高度差
        if (leftHeight == -1 || rightHeight == -1) return -1;   // 中
        if (abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return 1 + max(leftHeight, rightHeight); // 父节点 + 其子树的高度
        }
    }
    bool isBalanced(TreeNode* root) {
        if (getHeight(root) == -1) return false;
        return true;
    }
};

// 不断简化二
class Solution {
public:
    int getHeight(TreeNode* node) {
        if (node == NULL) return 0;
        int leftHeight = getHeight(node->left);   // 左
        int rightHeight = getHeight(node->right); // 右
        if (leftHeight == -1 || rightHeight == -1) return -1;   // 中
        if (abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return 1 + max(leftHeight, rightHeight); // 父节点 + 其子树的高度
        }
    }
    bool isBalanced(TreeNode* root) {
        if (getHeight(root) == -1) return false;
        return true;
    }
};

// 不断简化三
class Solution {
public:
    // -1 表示已经不是平衡二叉树了，否则返回值是以该节点为根节点树的高度
    int getHeight(TreeNode* node) {
        if (node == NULL) return 0;
        int leftHeight = getHeight(node->left);   // 左
        if (leftHeight == -1) return -1;
        int rightHeight = getHeight(node->right); // 右
        if (rightHeight == -1) return -1;
        return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1 ? false : true;
    }
};

迭代法（不是很熟练）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {

// 迭代法：请注意区别，在求最大深度的时候，因为求根节点的高度即为树的最大深度，因此可以通过后序遍历来求高度，进而等价于求最大深度。
// 在求最大深度的题目中，可以使用层序遍历来求深度，但是就不能直接用层序遍历来求高度了，这就体现出求高度和求深度的不同。（前序遍历，中左右的顺序，可以通过队列来模拟广搜，也是层序遍历的模板）
// 本题的迭代方式可以先定义一个函数，专门用来求高度。这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）

private:
    // cur节点的最大深度，就是cur的高度
    int getDepth(TreeNode* cur) {
        stack<TreeNode*> st;
        if (cur != NULL) st.push(cur);
        int depth = 0;   // 记录深度
        int result = 0;
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);  // 中
                st.push(NULL);
                depth++;
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);  // 左
            } else {
                st.pop();
                node = st.top();
                st.pop();
                depth--;
            }
            result = result > depth ? result : depth;
        }
        return result;
    }
    
public:
    bool isBalanced(TreeNode* root) {
        stack<TreeNode*> st;
        if (root == NULL) return true;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();   // 中
            st.pop();
            // 判断左右孩子高度是否符合
            if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {
                return false;
            }
            if (node->right) st.push(node->right);  // 右（空节点不入栈）
            if (node->left) st.push(node->left);    // 左（空节点不入栈）
        }
        return true;
    }
};

四、LeetCode257. 二叉树的所有路径

https://leetcode.cn/problems/binary-tree-paths/

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1：
输入：root = [1,2,3,null,5] 输出：["1->2->5","1->3"]
示例 2：
输入：root = [1] 输出：["1"]
提示：
树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    // version 1
    void traversal (TreeNode* node, vector<int>& path, vector<string>& res) {
        // 递归终止条件 到达叶子节点
        if (node->left == NULL && node->right == NULL) {
            path.push_back(node->val);   // 将最后一个节点加入路径中
            string sPath;
            for (int i = 0; i < path.size() - 1; i++) {
                sPath += to_string(path[i]);
                sPath += "->";
            }
            sPath += to_string(path[path.size() - 1]);
            res.push_back(sPath);
            return;
        }
        // 中，当前节点
        path.push_back(node->val);
        // 左
        if (node->left) {
            traversal(node->left, path, res);
            path.pop_back();   // 回溯
        }
        // 右
        if (node->right) {
            traversal(node->right, path, res);
            path.pop_back();   // 回溯
        }
    }
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;
        vector<int> path;
        if (root == NULL) return res;
        traversal(root, path, res);
        return res;
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    // version 2 版本一的精简版，省略了体现回溯的逻辑
private:
    void traversal(TreeNode* node, string path, vector<string>& res) {
        if (node->left == NULL && node->right == NULL) {
            path += to_string(node->val);
            res.push_back(path);
            return ;
        }
        // 中
        path += to_string(node->val);
        if (node->left) traversal(node->left, path + "->", res);  // 左
        if (node->right) traversal(node->right, path + "->", res); // 右
    }
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        string path;
        vector<string> res;
        if (root == NULL) return res;
        traversal(root, path, res);
        return res;

    }
};

迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    // version3 迭代法 除了模拟递归需要一个栈，同时还需要一个栈来存放对应的遍历路径
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        stack<TreeNode*> treeSt;  // 保存树的遍历节点
        stack<string> pathSt;     // 保存遍历路径的节点
        vector<string> res;       // 保存最终路径集合
        if (root == NULL) return res;
        treeSt.push(root);
        pathSt.push(to_string(root->val));
        while (!treeSt.empty()) {
            TreeNode* node = treeSt.top(); treeSt.pop();    // 取出节点 中
            string path = pathSt.top(); pathSt.pop();    // 取出该节点对应的路径
            // 遇到叶子节点
            if (node->left == NULL && node->right == NULL) {
                res.push_back(path);
            }
            // 右
            if (node->right) {
                treeSt.push(node->right);
                pathSt.push(path + "->" + to_string(node->right->val));
            }
            // 左
            if (node->left) {
                treeSt.push(node->left);
                pathSt.push(path + "->" + to_string(node->left->val));
            }
        }
        return res;
    }
};

五、LeetCode404.左叶子之和

https://leetcode.cn/problems/sum-of-left-leaves/

示例1：

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：（如上图）
输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24
示例 2:
输入: root = [1] 输出: 0
提示:
节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
// 判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。
    int sumOfLeftLeaves(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right == NULL) return 0; // 叶子节点（剪枝，减少递归）
        int leftNum = sumOfLeftLeaves(root->left);   // 左
        // 左子树就是一个左叶子的情况
        if (root->left && root->left->left == NULL && root->left->right == NULL ) {
            leftNum = root->left->val;
        }
        int rightNum = sumOfLeftLeaves(root->right);  // 右
        int sum = leftNum + rightNum;   // 中
        return sum;
    }
};


class Solution {
public:
// 递归精简版
    int sumOfLeftLeaves(TreeNode* root) {
        if (root == NULL) return 0;
        if (!root->left && !root->right) return 0;
        int leftNum = 0;
        if (root->left && !root->left->left && !root->left->right) {
            leftNum = root->left->val;
        }
        return leftNum + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);

    }
};

迭代法：

class Solution {
// 迭代法——使用前中后序都是可以的，只要把左叶子节点统计出来，就可以了。以前序遍历为例
public:
    int sumOfLeftLeaves(TreeNode* root) {
        stack<TreeNode*> st;
        if (root == NULL) return 0;
        st.push(root);
        int res = 0;
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            if (node->left && !node->left->left && !node->left->right) {
                res += node->left->val;
            }
            if (node->left) st.push(node->left);
            if (node->right) st.push(node->right);
        }
        return res;
    }
};

总结：

  1. 看完视频对于二叉树求最大/最小深度、高度题目有了新的理解，这应该是今天的重要收获！

  1. 尽管简化版代码真的很简单，但是背代码不是最终的目标，刷题的意义在于理解真正的实现逻辑和思路，能够写出易懂的复杂代码，等到后面熟悉之后，自然而然能化繁为简，简化代码的行数。

  1. 杜绝浮躁，踏踏实实刷题，这样的状态坚持住嗷，也希望通过博客记录的方式不断督促自己呢

  1. 以前非常不敢刷树的题目，感觉思路理解，一写就废。但是这几天的集中训练下来，收获多多~

  1. 进度是越来越跟不上啦，这周末看来又要加班嗷

刷题加油鸭~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/196984.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

jvm垃圾收集器有哪些

jvm垃圾收集器有哪些

Serial收集器 Serial收集器是最基本&#xff0c;发展最悠久的收集器&#xff0c;在JDK1.3.1之前是虚拟机新生代垃圾回收的唯一选择。这个收集器是一个单线程的。它的单线程的意义并不仅仅说明它只会使用一个CPU或者一条收集线程去完成收集工作&#xff0c;最重要的是&#xff…
阅读更多...
量化选股股票和量化交易的两者有什么区别？

量化选股股票和量化交易的两者有什么区别？

最近a股在频繁波动后终于开始走强。近几个月来&#xff0c;一些净值明显下降的量化产品业绩终于实现了阶段性回升。与此同时&#xff0c;根据金融终端&#xff0c;量化私募管理的规模已经超过1万亿元。面对目前市场上大量超额收益和大幅波动带来的不合理定价带来的收益&#xf…
阅读更多...
磨金石教育摄影技能干货分享｜春节街拍欣赏：大街上的年味

磨金石教育摄影技能干货分享｜春节街拍欣赏：大街上的年味

当然还有很多人依然沉浸在过年的喜庆氛围中&#xff0c;我们一般把除夕到十五这个期间段都归入春节期间。在这个时间段内街道上都是喜庆的氛围热热闹闹&#xff0c;年味十足。过了除夕之后&#xff0c;春节娱乐的主题除了走亲访友&#xff0c;就是出行了。春节小长假&#xff0…
阅读更多...
jmeter脚本处理加密验签

jmeter脚本处理加密验签

一 、账号密码加密 1.1 背景&#xff1a; 一个登录接口&#xff0c;账号是明文传输&#xff0c;但是密码要先经过加密&#xff0c;再做传输。 比如&#xff1a; 一个用户&#xff0c;账号为123465 密码为 abcde 实际上登录接口&#xff0c;请求&#xff0c;传参为 账号 1…
阅读更多...
使用傅里叶级数展开法从谐波的和中产生方波（Matlab代码实现）

使用傅里叶级数展开法从谐波的和中产生方波（Matlab代码实现）

目录 &#x1f4a5;1 概述 &#x1f4da;2 运行结果 &#x1f389;3 参考文献 &#x1f468;‍&#x1f4bb;4 Matlab代码 &#x1f4a5;1 概述 谐波是指对周期性非正弦交流量进行傅里叶级数分解所得到的大于基波频率整数倍的各次分量&#xff0c;通常称为高次谐波&#xf…
阅读更多...
C++11 可变参数模板

C++11 可变参数模板

作者&#xff1a;小萌新 专栏&#xff1a;C进阶 作者简介&#xff1a;大二学生 希望能和大家一起进步&#xff01; 本篇博客简介&#xff1a;介绍C11的可变参数模板 可变参数模板可变参数模板的概念可变参数模板的定义方式参数包两种解开方式递归展开参数包逗号表达式展开参数包…
阅读更多...
Springboot在线考试管理系统

Springboot在线考试管理系统

一、项目简介 本项目是一套基于Springboot在线考试管理系统&#xff0c;主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Java学习者。 包含&#xff1a;项目源码、数据库脚本等&#xff0c;该项目附带全部源码可作为毕设使用。 项目都经过严格调试&#xff0c;…
阅读更多...
java基于springboot+vue的校园跑腿系统

java基于springboot+vue的校园跑腿系统

随着我国教育制度的改革的发展&#xff0c;各大高校的学生数量也在不断的增加。当前大学生的生活和消费习惯等导致他们更喜欢通过网络来获取自己想要的商品和服务&#xff0c;这也是导致当前校园跑腿盛行的主要原因。为了能够让更多的学生享受到校园跑腿的服务&#xff0c;我们…
阅读更多...
中睿天下荣获中国网络安全产业联盟（CCIA）2022年度先进会员单位奖

中睿天下荣获中国网络安全产业联盟（CCIA）2022年度先进会员单位奖

近日&#xff0c;中国网络安全产业联盟&#xff08;CCIA&#xff09;发布“关于2022年度表彰先进的决定”&#xff0c;对在联盟工作中做出积极贡献的会员单位进行表彰&#xff0c;中睿天下荣获中国网络安全产业联盟“2022年度先进会员单位“奖。中国网络安全产业联盟成立于2015…
阅读更多...
Linux基本使用

Linux基本使用

文章目录1. Linux 基本命令文件内容查看命令wget下载tar.gz文件tar压缩解压缩yum2. 安装node/npm下载解压配置环境变量设置npm代理3. 权限1. Linux 基本命令 ls&#xff1a;用来查看当前目录文件 # 查看隐藏文件 -a ls -a # 查看详细信息 -l 简写为 ll ls -l ll # 查看指定目…
阅读更多...
Docker - 8. Docker镜像底层原理

Docker - 8. Docker镜像底层原理

目录 1. 镜像是什么 2. UnionFS 联合文件系统 3. Docker镜像加载原理 4. Docker 容器和镜像的底层关系 5. Docker 镜像 commit 操作案例 1. 镜像是什么 Docker 镜像是一个特殊的文件系统&#xff0c;除了提供容器运行时所需的程序、库、资源、配置等文件外&#xff0c;还…
阅读更多...
漏洞深度分析|Apache iotdb-web-workbench 认证绕过漏洞（CVE-2023-24830）分析

漏洞深度分析|Apache iotdb-web-workbench 认证绕过漏洞（CVE-2023-24830）分析

项目介绍 IoTDB-Workbench是IoTDB的可视化管理工具&#xff0c;可对IoTDB的数据进行增删改查、权限控制等。 项目地址 https://github.com/apache/iotdb-web-workbench 漏洞概述 Apache iotdb-web-workbench 由于硬编码了jwt token加密密钥&#xff0c;导致攻击者可以伪造t…
阅读更多...
数仓之缓慢变化维(拉链表)

数仓之缓慢变化维(拉链表)

文章目录缓慢变化维拉链表 -- 理论缓慢变化维解决方案&#xff1a;拉链表场景&#xff1a;拉链表缺点&#xff1a;拉链表查询优化&#xff1a;拉链表 -- 示例sql查询方式补充流水表全量表增量表缓慢变化维 什么是缓慢变化维? 缓慢变化维&#xff0c;简称SCD&#xff08;Slowl…
阅读更多...
科技云报道：上云尚未成功，“下云潮”已悄然来临？

科技云报道：上云尚未成功，“下云潮”已悄然来临？

科技云报道原创。 云计算一直被视为是企业数字化转型的底座&#xff0c;很多企业都在通过加速数字化转型应对市场环境的动荡变化&#xff0c;一手抓降本增效&#xff0c;另一手也还在继续谋求突破式创新。 然而&#xff0c;经历这两年的疫情&#xff0c;活下去成为每一个企业的…
阅读更多...
【js逆向 | 网络爬虫】简单 js 逆向实践，获取邮箱地址

【js逆向 | 网络爬虫】简单 js 逆向实践，获取邮箱地址

网站&#xff1a; https://australia51.com/citywide/ 在各个城市分类下&#xff0c;可以看到商家链接 而部分商家介绍中&#xff0c;含有邮箱 我们通过 f12 检查元素&#xff0c;发现邮箱字段在 html 里面。 但是抓包发现&#xff0c;该字段是 <a href"/cdn-cg…
阅读更多...
Anaconda环境Python中xlrd库的配置方法

Anaconda环境Python中xlrd库的配置方法

本文介绍在Anaconda环境下&#xff0c;安装Python读取.xls格式表格文件的库xlrd的方法。 首先需要说明的是&#xff0c;由于xlrd库在读取.xlsx格式文件时具有安全漏洞&#xff0c;因此在其2.0.0及以后的版本中&#xff0c;只能读取.xls格式的表格文件&#xff1b;如果需要读取其…
阅读更多...
C语言中字符串库函数

C语言中字符串库函数

目录1.求字符串长度strlen模拟实现strlen2.长度不受限制的字符串函数strcpy模拟实现strcpystrcat模拟实现strcatstrcmp模拟实现strcmp3.长度受限制的字符串函数介绍strncpy模拟实现strncpystrncat模拟实现strncatstrncmp模拟实现strncmp4.字符串查找strstr模拟实现strstrstrtok…
阅读更多...
POE交换机全方位解读（下）

POE交换机全方位解读（下）

POE供电在安防系统中的应用 安防行业应用PoE组网主要有简化布线、节能灵活、安全方便等优势。众所周知&#xff0c;一般的网络摄像机除了需要通过网线来传输视频信号外&#xff0c;还必须全天候为其提供足够的电力。而在现实施工中&#xff0c;经常会出现因为无法提供稳定的电源…
阅读更多...
[SSL]微信实机测试 request:fail -2:netLERR_FAILED

[SSL]微信实机测试 request:fail -2:netLERR_FAILED

request:fail -2:netLERR_FAILED 微信小程序开发过程中&#xff0c;实机测试调用服务器链接报错。 SSL证书已安装&#xff0c;通过下面工具检查&#xff0c;中间证书安装有问题。 下面是检查证书链和补全证书链的工具网站&#xff0c;亲测有效。 w​​​​​​​​​​​​​…
阅读更多...
[数仓]埋点数据接入

[数仓]埋点数据接入

第40个视频的1&#xff1a;03&#xff1a;31一、采集flume日志服务器&#xff1a;将日志采集到本地&#xff0c;共有两个日志服务器&#xff0c;因此要安装两台flume&#xff0c;每个flume采集其所在服务器上的日志source:taildir source可以实时的读取文件中的数据&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023