目录

主要内容   

  模型研究   

  结果一览   

下载链接 

---

主要内容   

仿真程序参考文献《改进粒子群算法的永磁同步电机多参数辨识》，采用粒子群算法与simulink模型结合的方式，对永磁同步电机进行多参数辨识。程序以定子绕组电阻、d轴电感、q轴电感和永磁体磁链四个参数作为输入参数，以定子dg轴电压作为输出，通过辨识模型电压与测量电压的偏差作为目标函数，从而实现参数的精准辨识。

  模型研究   

1. 适应度函数

适应度函数以辨识模型与实际测量值之间的误差平方和最小为目标，适应度函数值越小，其辨识模型电压与测量电压越接近，待辨识参数和实际值也越接近，具体表达式如下：

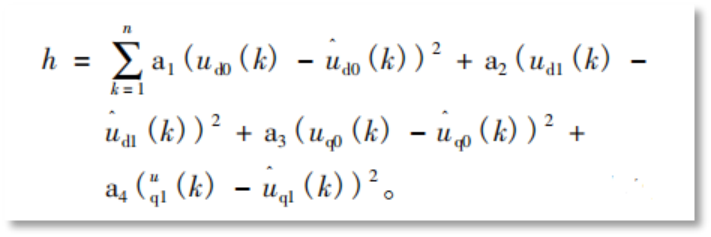
对应的程序代码为：

fitness_gbest(j) = -((ud0-ud_0)^2 + (uq0-uq_0)^2 + (ud1-ud_1)^2 + (uq1-uq_1)^2 ); % 每个个体的历史最佳适应度

2. 算法流程

算法流程主要是通过粒子群算法调用simulink仿真模型，通过输入计算输出值和适应度值，通过循环优化出最佳参数，具体流程可参考下图：

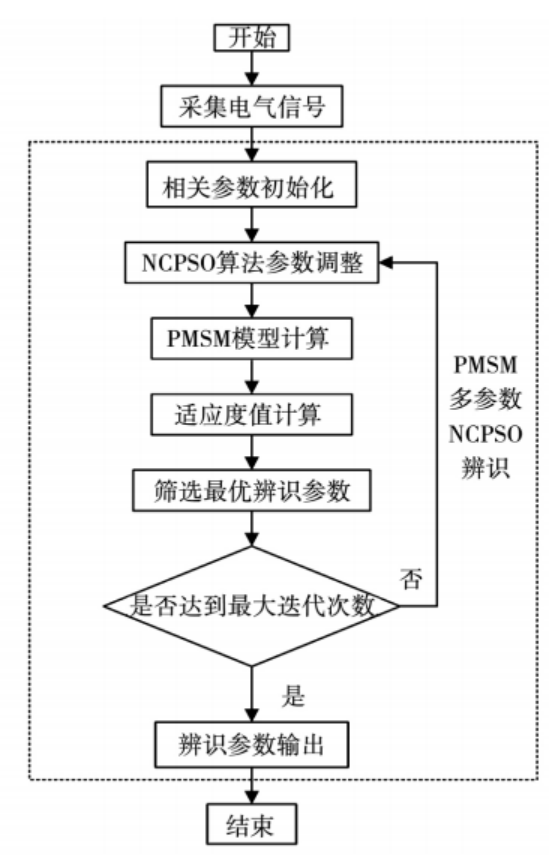
3. simulink仿真模型主体

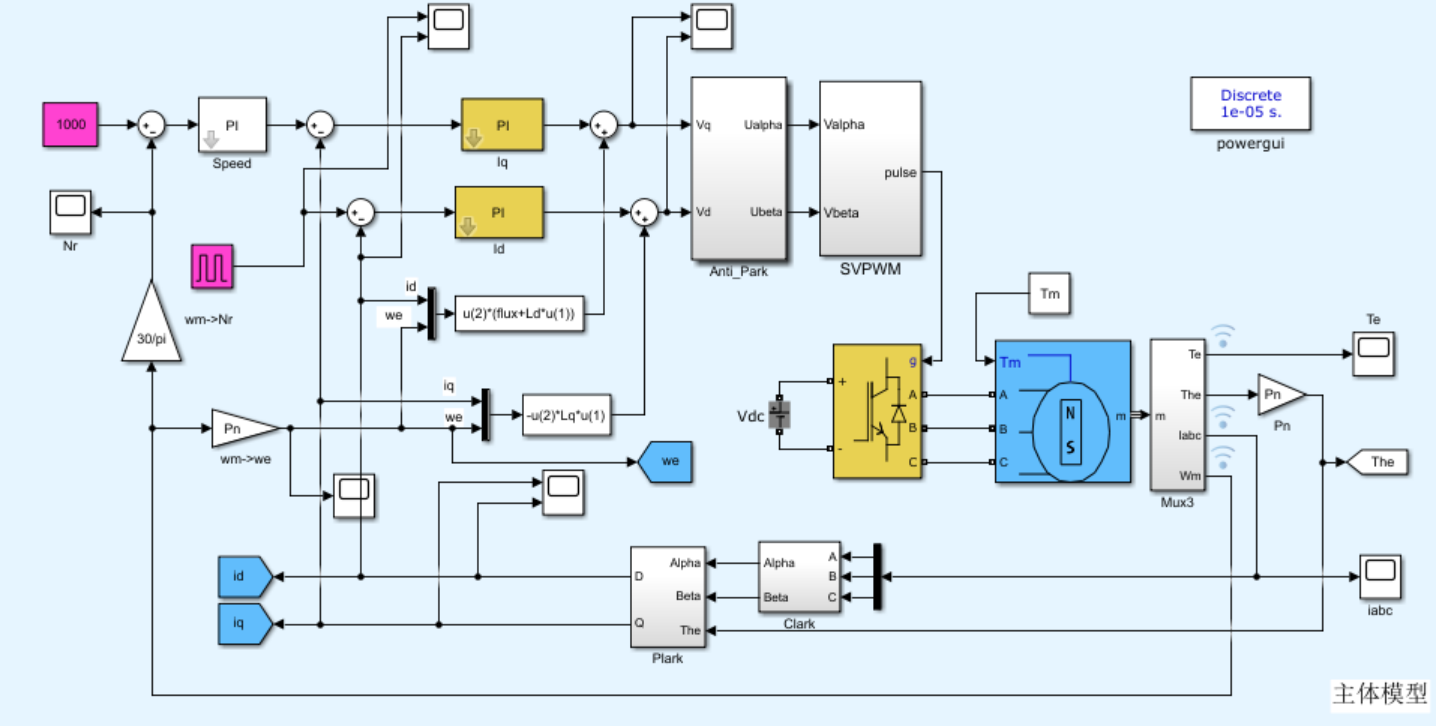
对应数据采集模块的​模型如下：

模型对应的dq轴电压计算模块如下​：

SVPWM模块​如下：

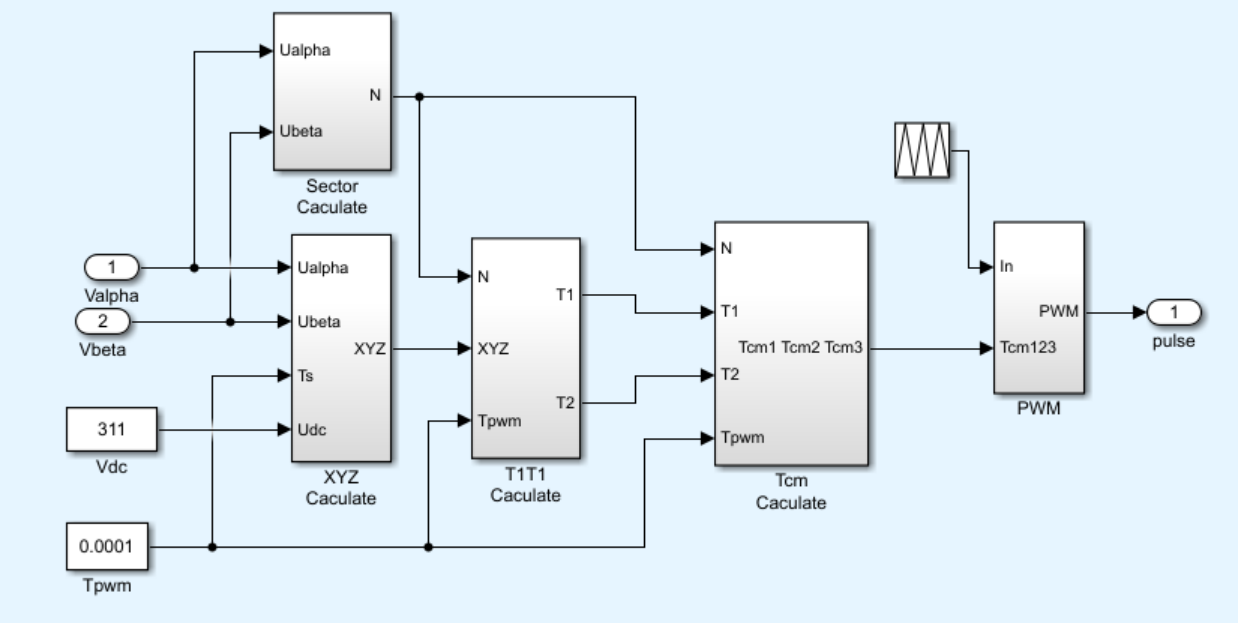
4. 部分程序代码

​
iter = 1;                        %迭代次数
record = zeros(ger, 1);          % 记录器
while iter <= ger
    for j=1:sizepop
        %    更新速度并对速度进行边界处理 
        pop_v(:,j)= c_1 * pop_v(:,j) + c_2*rand*(gbest(:,j)-pop_x(:,j))+c_3*rand*(zbest-pop_x(:,j));% 速度更新
        for i=1:dim
            if  pop_v(i,j) > vlimit_max(i)
                pop_v(i,j) = vlimit_max(i);
            end
            if  pop_v(i,j) < vlimit_min(i)
                pop_v(i,j) = vlimit_min(i);
            end
        end
        
        %    更新位置并对位置进行边界处理
        pop_x(:,j) = pop_x(:,j) + pop_v(:,j);% 位置更新
        for i=1:dim
            if  pop_x(i,j) > xlimit_max(i)
                pop_x(i,j) = xlimit_max(i);
            end
            if  pop_x(i,j) < xlimit_min(i)
                pop_x(i,j) = xlimit_min(i);
            end
        end
        
        %    进行自适应变异
        if rand > 0.85
            i=ceil(dim*rand);
            pop_x(i,j)=xlimit_min(i) + (xlimit_max(i) - xlimit_min(i)) * rand;
        end
  
        %    进行约束条件判断并计算新种群各个个体位置的适应度
        ud_0 = pop_x(1,j)*id0 - we0*pop_x(3,j)*iq0;
        uq_0 = pop_x(1,j)*iq0 + we0*(pop_x(2,j)*id0 + pop_x(4,j));
        ud_1 = pop_x(1,j)*id1 - we1*pop_x(3,j)*iq1;
        uq_1 = pop_x(1,j)*iq1 + we1*(pop_x(2,j)*id1 + pop_x(4,j));
        fitness_pop(j) = -((ud0-ud_0)^2 + (uq0-uq_0)^2 + (ud1-ud_1)^2 + (uq1-uq_1)^2 ); 

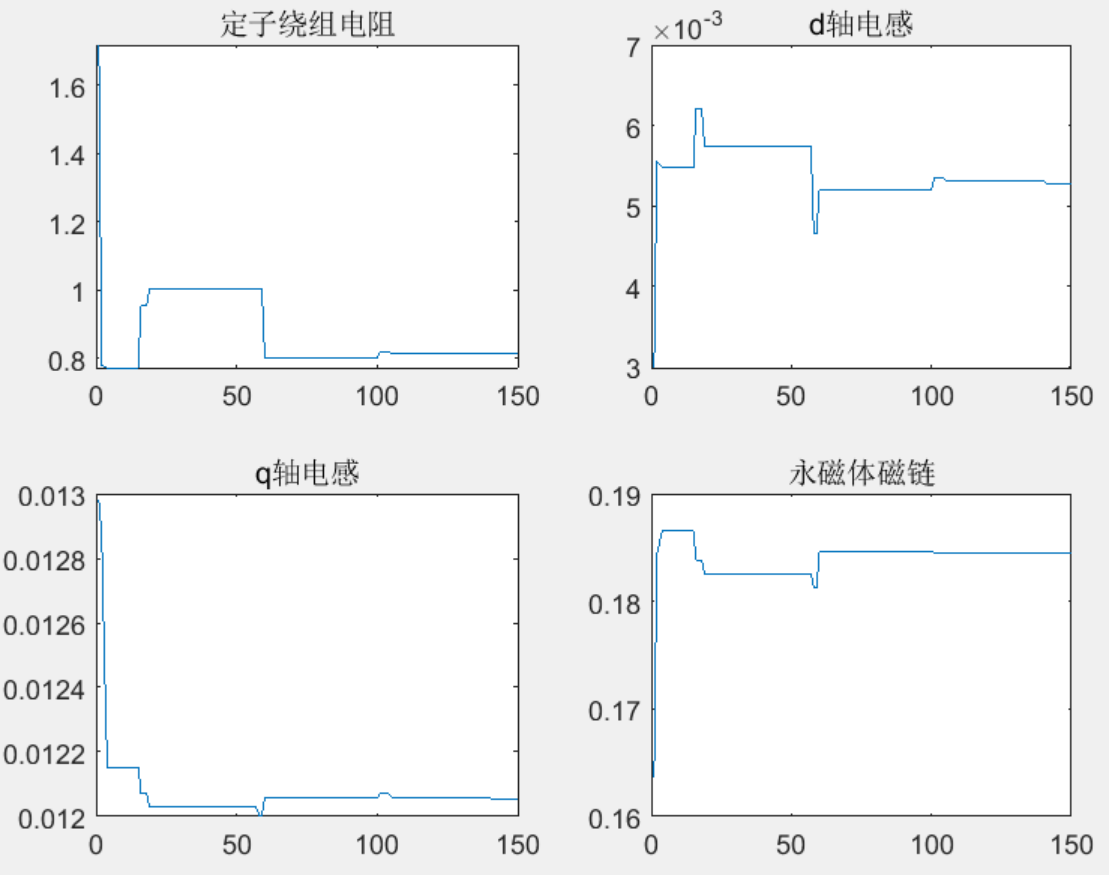
  结果一览   

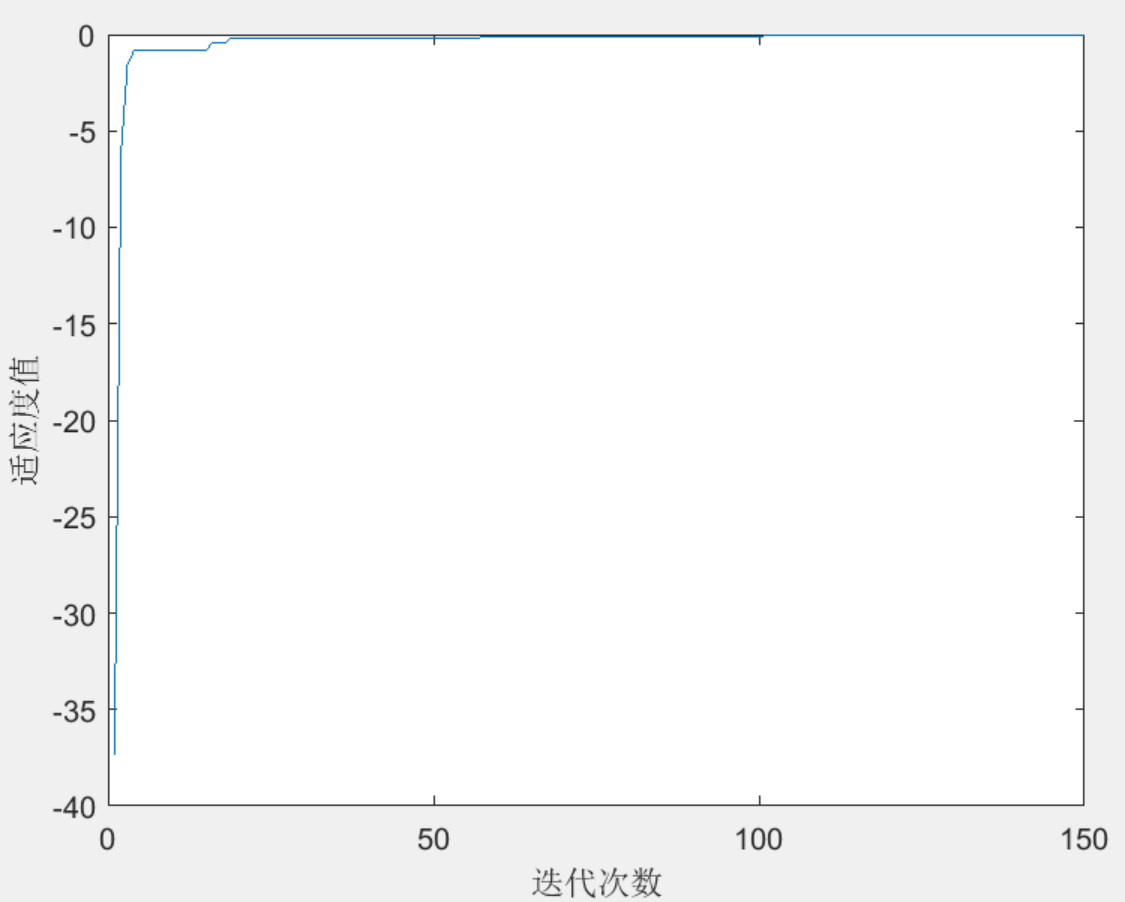
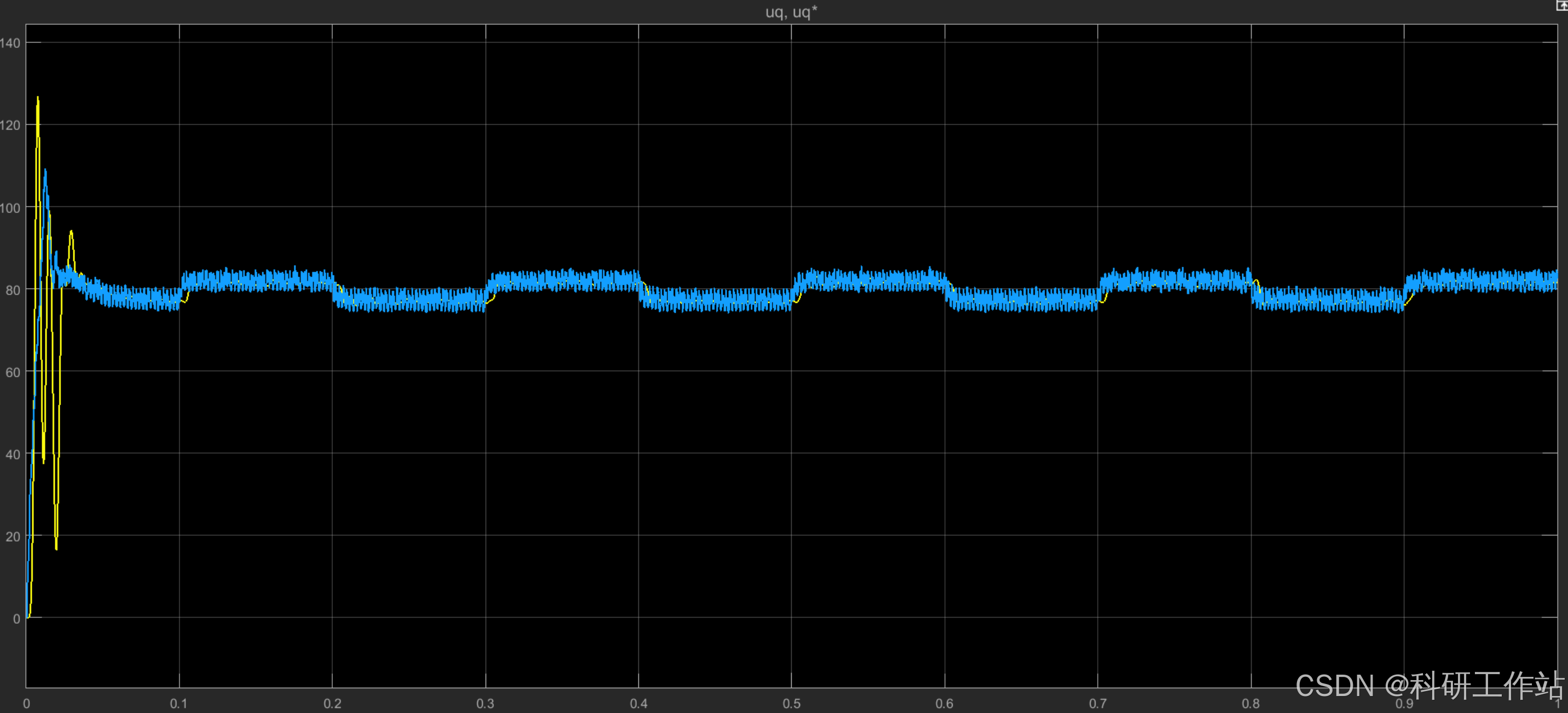
适应度值逐渐逼近0，说明待辨识参数和实际值越来越近，优化​效果非常好！

Ud

Uq​

 

下载链接