快速排序

前言
快速排序算法是最流行的排序算法,且有充足的理由,因为在大多数情况下,快速排序都是最快的。所以学习快速排序算法十分有必要。当然,既然它这么好,也就不太容易理解。
正文
Hoare版快排
快速排序是Hoare在1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
既然是二叉树结构,在这个重复过程中就少不了是递归:

递归到什么程度?递归到只有一个数据或者没有数据,就开始“归”。
在头文件中我们对快速排序的声明如下:
void QuickSort(int* arr, int left, int right);
说明了我们需要传的参数是待排序的数组,以及左和右两个下标控制要排序的区间。
快速排序算法的具体实现
首先,我们要对left和right控制的区间找基准值。因为找到了基准值后,我们就能控制下一次递归的区间。
怎么找基准值?我们上面说基准值要满足左侧数据都小于基准值,右侧数据都大于基准值,所以我们从这一点入手。
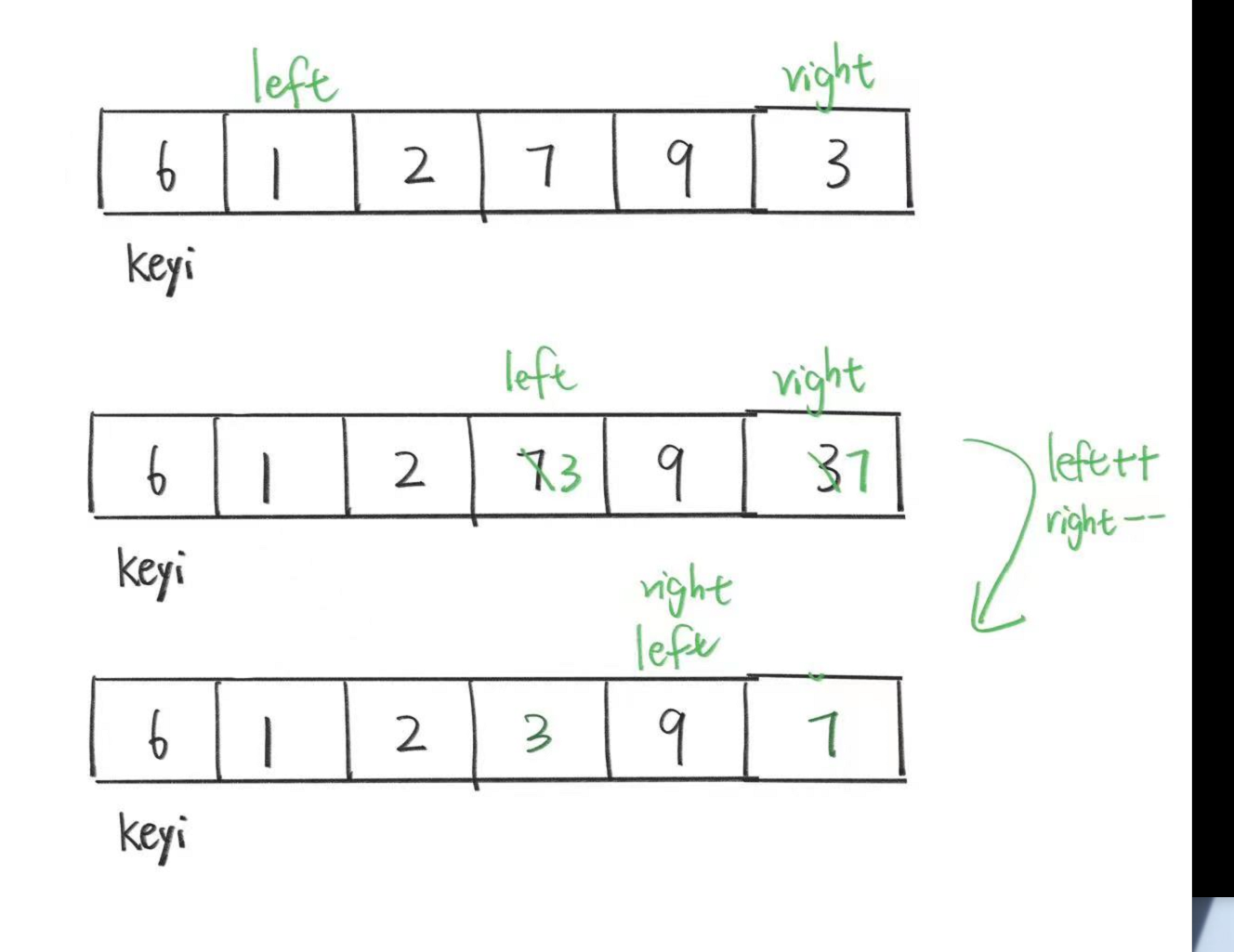
我们现在有一个数组,我们让基准值先为第一个数据,让left为第二个数据,right为最后一个数据。然后,让left从左到右找比基准值大的数据,让right从右往左找比基准值小的数据。
找到后,我们让left和right的值交换;交换完再重复刚才的过程。

然后我们发现left走到right的后面去了, 这时我们让keyi和right交换,最后keyi就来到了正确的位置。检查一下,基准值左侧都是比基准值要小的数据,基准值右侧都是比基准值要大的数据。
现在我们在代码中实现找基准值,我们写一个QuickSort的子方法,就叫做_QuickSort,参数还是一样的。
(注意,在写快排代码的过程中,等于的情况会比较难处理,需要单独讨论,我们可以先跳过,到后面再来仔细讨论)
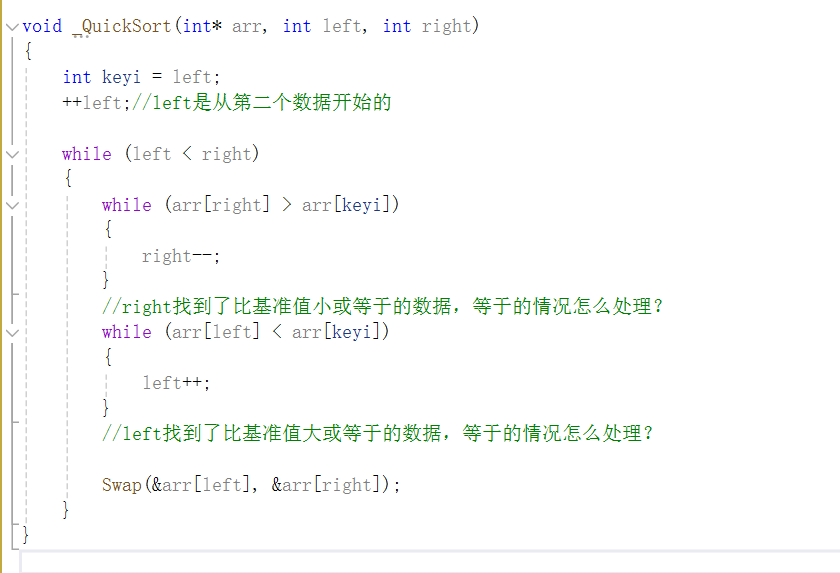
我们可以先写出这样的代码,left比right小进入循环,right从右往左找比基准值小的,left从左往右找比基准值大的,找到了就交换,这样逻辑顺下来写的代码似乎没有问题,实则有一个错误。
其实上面代码的运行逻辑是这样的:

在第一次循环后我们的left<right是满足的,所以再次进入循环,找到了新的left和right,但是此时的left已经比right大了,我们想要的是在此时将right与keyi交换,但是现在我们会执行left与right交换,然后终止循环。
所以我们不能直接交换,要在交换之前进行判断。
(注意函数的返回值是int,我们要把找到的基准值下标返回)
int _QuickSort(int* arr, int left, int right)
{
int keyi = left;
++left;//left是从第二个数据开始的
while (left < right)
{
while (arr[right] > arr[keyi])
{
right--;
}
//right找到了比基准值小或等于的数据,等于的情况怎么处理?
while (arr[left] < arr[keyi])
{
left++;
}
//left找到了比基准值大或等于的数据,等于的情况怎么处理?
if (left < right)//等于的情况怎么处理?
{
Swap(&arr[left], &arr[right]);
}
}
//right与keyi交换
Swap(&arr[keyi], &arr[right]);
return right;
}
但是这是我们还没有仔细分析要不要取等的版本。
为了探讨等于情况,我们就需要更多的案例。
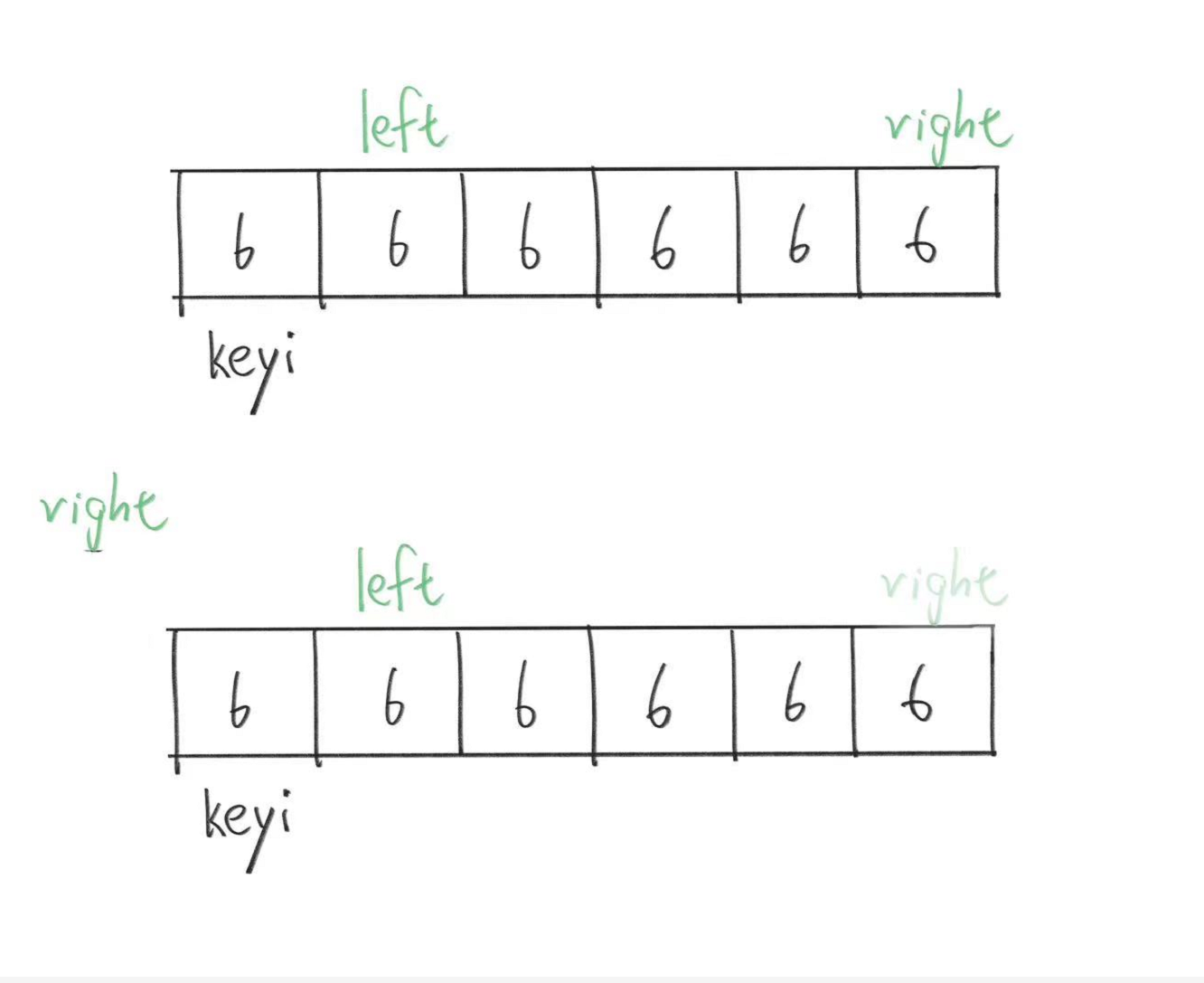
假如我们现在就必须要让right找到比keyi小的才停下来,也就是改为这样:
while (arr[right] >= arr[keyi])//这里改为了大于等于
{
right--;
}
等于也还要往前走。
我们发现我们没有限制,所以right会一直走到越界,于是我们需要加上限制,让right顶多走到left前一个:
while (left<=right && arr[right] >= arr[keyi])//注意限制
{
right--;
}

所以我们的left也不能一直往后走,要加上限制。
while (left < right)//我们先写为可以等于
{
while (left<=right && arr[right] >= arr[keyi])//注意限制
{
right--;
}
while (left <= right && arr[left] <= arr[keyi])
{
left++;
}
if (left <= right)//我们先写为可以等于
{
Swap(&arr[left], &arr[right]);
}
}
(注意在上述代码中我们让外层循环可以取等,让内层的if也可以取等,总之就是都让等,看看情况)
加上这个限制后,在我们举的这个例子中,right已经走到left前面去了,所以内层的第二个while循环我们是进不去了,退出循环,来到right与keyi交换的语句。
根据上面画的图,此时我们的keyi和right都在第一个6的位置。而我们找基准值的意义是要划分左子序列和右子序列。
一般情况,左子序列的区间为[left,keyi-1],右子序列为[keyi+1,right],但是此时我们基准值在第一个数位置,所以我们就没有左子序列了,剩下右边全是右子序列。
我们要再次递归划分子序列,而因为数据全是6,下一次划分的情况又是一样的,基准值又是第一个数。所以我们排完n个数据排n-1个数据,然后n-2个数据,所以我们要递归n次,而且每次都要排n-1 、n-2 、n-3个数据,所以时间复杂度就很差。而我们前面讲快排应该每次都以“二分”来排序所以才那么快。
那么,怎么解决这个问题或者说代码应该怎么优化呢?
while (left <= right)//这里先写为可以等于
{
while (left<=right && arr[right] > arr[keyi])//改为>,也就是等于时无法进入循环往前走
{
right--;
}
while (left <= right && arr[left] < arr[keyi])//改为<
{
left++;
}
if (left <= right)//这里先写为可以等于
{
Swap(&arr[left++], &arr[right--]);//改为了要++和--
}
}
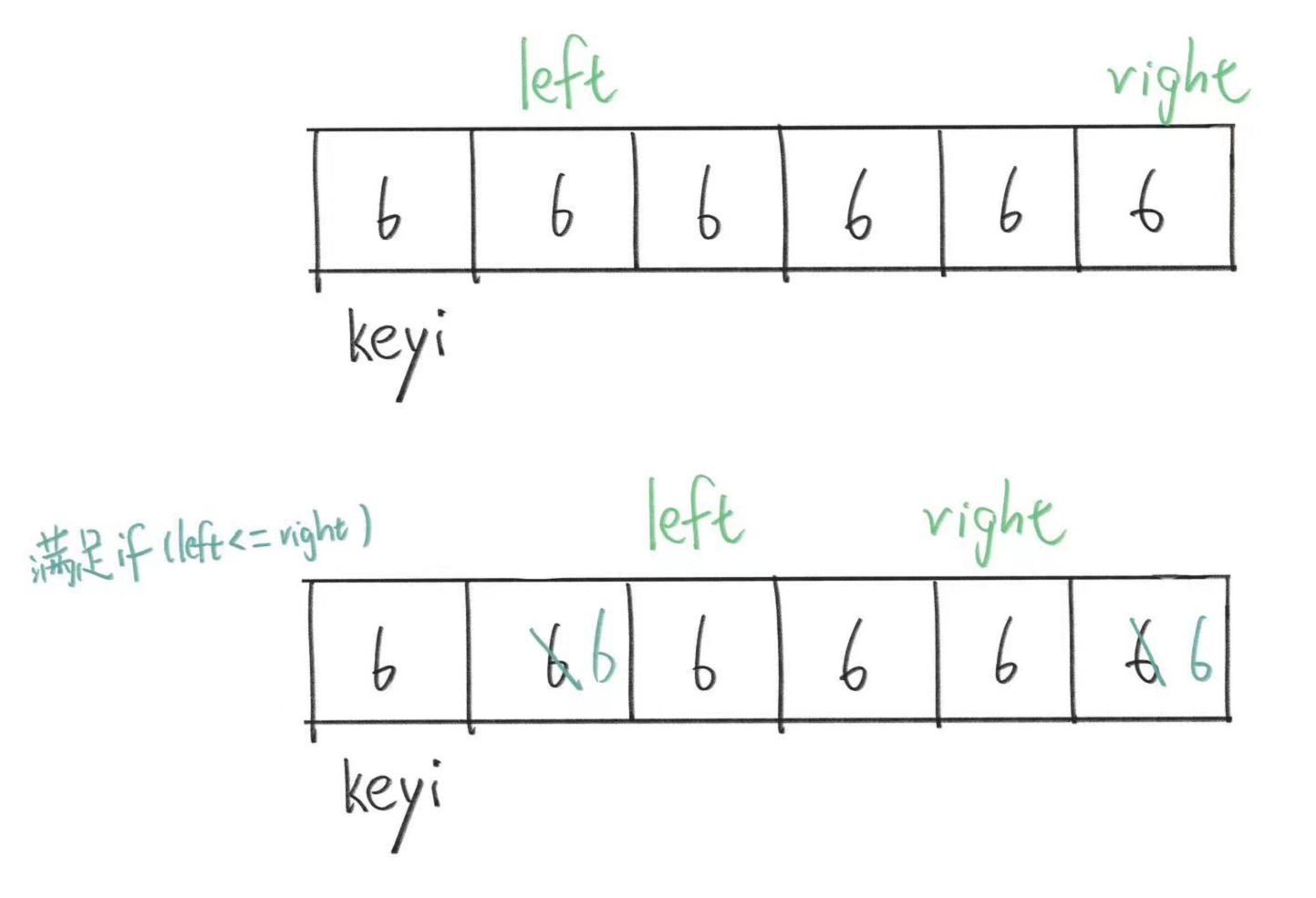
所以这是我们现在代码的执行情况,然后left此时<=right所以我们再次进入循环,接着我们重复这个过程。
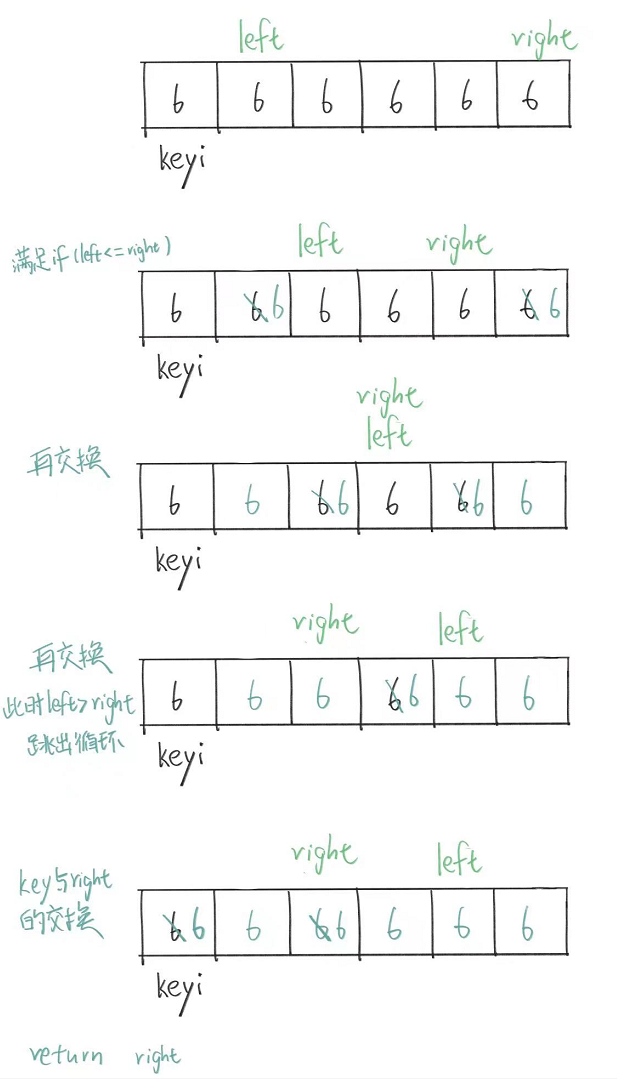
如图。
可以看到我们这么做的原因就是为了尽可能让基准值来到中间的位置,从而划分小的子序列。
现在我们再看一个场景:相遇值大于keyi值
(这个场景解释了为什么外循环是while (left <= right)而不是while (left < right),也就是说为什么left与right相遇时还要再进入循环。
可以看到,如果我们写的是while (left < right),那么无法再进入循环,也就会执行
//right与keyi交换
Swap(&arr[keyi], &arr[right]);
return right;
那么我们就让9到了第一个位置,而这不是我们想要的。所以我们要有等号,也就是相遇时也要进入循环让left再向左走一次,让right再向右走一次,然后再退出循环让right与keyi交换,所以内层left与right比较的代码也要能取等。
所以,两个内循环的第二个条件不能取等是为了防止基准值找到第一个数然后最终代码效率低下;left与right比较要取等是因为要防止把更大的数换到第一个位置。
现在我们的子程序,也就是找基准值的程序写完了。
我们还可以发现,基准值待的位置就是它该待的地方,所以下一次找基准值它的位置不用发生改变。
所以也可以这么说,找基准值的目的就是把基准值放到它该待的位置。
然后根据递归的思路,我们就可以写出快排的代码:
//快速排序
void QuickSort(int* arr, int left, int right)
{
if (left >= right)//这种情况没有子序列,不要递归
return;
//找基准值
int keyi = _QuickSort(arr, left, right);
QuickSort(arr, left, keyi - 1);
QuickSort(arr, keyi+1, right);
}
然后我们测试一下。
int main()
{
int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
int n = sizeof(a) / sizeof(int);
printf("排序前: ");
PrintArr(a, n);
QuickSort(a, 0, n-1);
printf("排序后: ");
PrintArr(a, n);
return 0;
}

测试代码:排序性能对比
在前面几种排序算法(前几篇博客)的探讨中我们都用到了10万个随机数的排序时间来检测排序速度,现在我们也再次使用这个方法(具体写法参考前面的文章)来检测一下快排的速度:
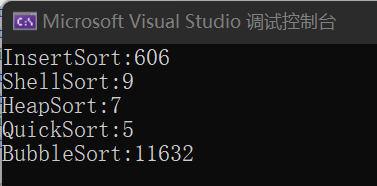
可以看到快排确实非常快。
现在我们改为100万个随机数据的排序,不看冒泡排序和直接插入了,来比较比较希尔排序、堆排序和快排的表现:

可以看到快排显著的优势。
快排的时间复杂度
我们知道快排是二叉树结构的交换排序方法,我们要递归logn次,空间复杂度为O(logn), 时间复杂度为O(nlogn)。可以看到空间复杂度和时间复杂度都很低。
其实快排还有其他版本,放到下篇文章再说=_=