目录
0.写在前面
1.什么是堆?
2. 堆排序
2.1 建堆
2.1.1 AdjustUp(向上调整算法)
2.1.2 AdjustDown(向下调整算法)
2.2 两种建堆算法的时间复杂度
2.2.1 AdjustUp建堆的时间复杂度
2.2.2 AdjustDown建堆的时间复杂度
2.3 排序
3.堆排序的时间复杂度
完整源码
0.写在前面
你是否对堆排序早有耳闻?身为经典排序算法中的佼佼者,我们着实有必要学习一下堆排序的实现。接下来我们就一起认识一下堆排序是如何依靠它优秀的结构及算法在众多的排序算法中脱颖而出的。
1.什么是堆?
堆是一种完全二叉树。只不过堆是二叉树顺序结构的实现,说白了就是将一个数组看作二叉树。也就是说,堆的逻辑结构是一棵二叉树,存储结构是数组。
堆又分为大堆和小堆:
大堆:树中所有父亲都大于等于孩子;
小堆:树中所有父亲都小于等于孩子。
注意,不满足这两点的二叉树不能称为堆(这点很重要)。

2. 堆排序
//堆排序
void HeapSort(int* a, int n)//a为数组首地址,n为数组大小
{
//堆排序的实现...
}
//测试函数
void HeapSortTest()
{
int arr[] = { 12,34,45,78,56,74,3,7,9,5 };
//进行堆排序
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
//打印排序之后的数组
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
}
实现堆排序分为两个步骤(这里默认对数组进行排序):
■ 建堆
■ 排序
2.1 建堆
在上一章节中,我介绍了两种建堆算法:向上调整算法、向下调整算法。这里我们再次认识一下这两种算法以及二者的差别。
2.1.1 AdjustUp(向上调整算法)
假设此刻有一个大堆,我们此刻需要将 60 进行向上调整。具体步骤是这样的:
 第一步,比较 60 与它父亲节点的大小。因为要保证插入数据之后堆仍然是大堆,所以如果 60 大于父亲,则交换位置。
第一步,比较 60 与它父亲节点的大小。因为要保证插入数据之后堆仍然是大堆,所以如果 60 大于父亲,则交换位置。

第二步,继续比较 60 与父亲的值,若大于父亲则交换位置。

至此,60 已经到它正确的位置上了。
以上就是向上调整的过程,来看看代码实现。
void AdjustUp(HPDataType* a, int child)//child为需要调整的数据的位置
{
int parent = (child - 1) / 2;
while (child > 0)
{
//建大堆用'>',小堆用'<'
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
认识了向上调整算法的思想以及实现,来看看如何用向上调整算法对数组建堆。
实现思路:从数组的第一个元素开始,按顺序对每一个元素都进行向上调整。既保证了每一个元素都到了合适的位置,还保了证在对某个元素进行向上调整的时候,该元素之前的数据是一个堆。
代码实现:
void HeapSort(int* a, int n)
{
//向上调整建堆
for (int i = 0; i < n; i++)
{
AdjustUp(a, i);
}
//排序...
}
2.1.2 AdjustDown(向下调整算法)
假设此刻要对 5 进行向下调整使其到达合适的位置。
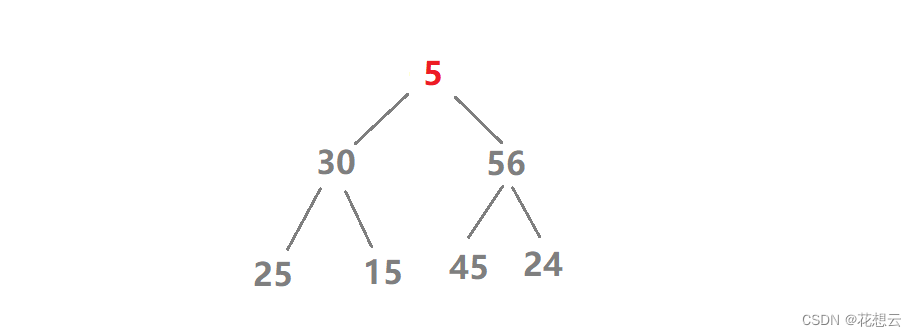
第一步,比较 5 和它的两个孩子中较大(是小堆就选小的)的那个,如果如果 5 小于该数字,就进行交换。

第二步,继续比较 5 和它的两个孩子中较大(是小堆就选小的)的那个,如果如果 5 小于该数字,就进行交换。
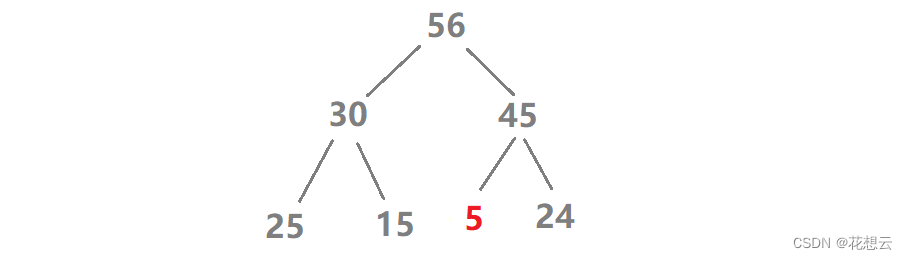
第三步,继续上述的比较,但是此刻 5 已经没有孩子了,就停止。而且发现 5 已经到达了正确的位置。
以上就是向下调整的过程,来看看代码的实现。
void AdjustDown(HPDataType* a, int n, int parent)
{
assert(a);
//先默认较大的为左孩子
int child = parent * 2+1;
while (child<n)
{
//如果右孩子比左孩子大,就++
if (a[child] < a[child + 1] && child + 1 < n)
{
child++;
}
//建大堆用'>',小堆用'<'
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
那么如何用向下调整算法进行建堆呢?此时建堆的方式与向上调整不同。向上调整是对数组从前往后调整,而向下调整却与之相反。
原因是,向上调整的时候看的是该位置之前的数据是否为堆;而向下调整则要保证该位置的左右子树是堆,所以必须得对数组从后往前进行调整。
实现思路:从数组最后一个数的父亲开始(因为堆的最后一排没有子树,无需调整),倒着对数组的每一个数进行向下调整。
代码实现:
void HeapSort(int* a, int n)
{
//向下调整建堆
for (int i = n - 1; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//排序...
}2.2 两种建堆算法的时间复杂度
既然两种建堆算法都可以完成建堆的任务,那么就需要比较一下二者的时间复杂度,择优录取。
2.2.1 AdjustUp建堆的时间复杂度
时间复杂度就是该算法在最坏情况下所需要的步数,那么以这样一棵满二叉树为例。
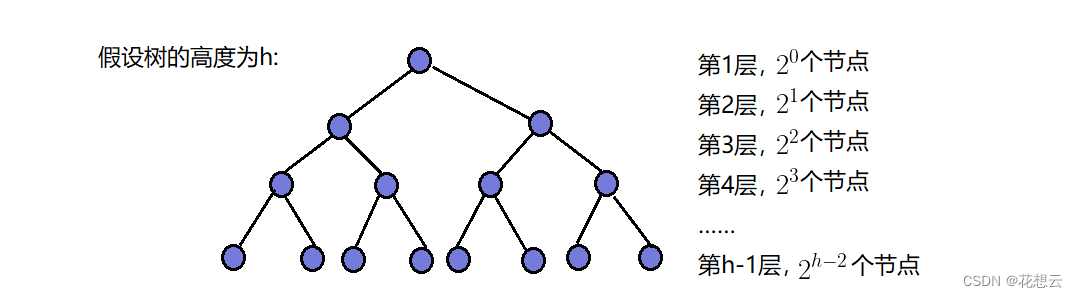
最坏情况下,每个节点都需要换到堆顶的位置。那么有这样的规律:
第1层节点:需要向上移动 0 层;
第2层节点:需要向上移动 1层;
......
第h-1层节点:需要向上移动 h-2 层;
第h层节点:需要向上移动 h-1 层;
所有节点的步数和为:T(h)=2^0*0+2^1^1+2^2*2+......+2^(h-2)*(h-2)+2^(h-1)*(h-1)=2^h*(2-h)-2。
另外代入之前见到的一个公式:结点数 n=h^2-1,即 h=log(n+1)。代入得:
T(n)=(n+1)*[2-log(n+1)]-2;
所以AdjustUp算法的时间复杂度用大O记法表示为 O(N*log N)。
2.2.2 AdjustDown建堆的时间复杂度
最坏情况下,依旧是一棵满二叉树。
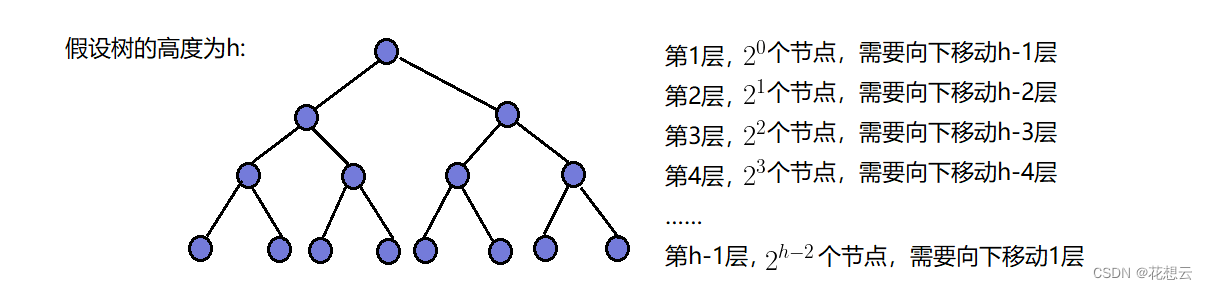
前文解释过,向下调整时最后一层的节点是不需要调整的,因为它们没有子树。所以前h-1层节点在最坏情况下所花费的步数和为:
T(h)=2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+......+2^(h-2)*1=2^h-h-1。
代入公式,h=log(n+1) 得:
T(n)=n-log(n+1);
所以,AdjustDown的时间复杂度为O(N)。
总结:对比二者的时间复杂度,我们还是选择向下调整建堆更优。其实不需要用仔细计算就大概可以比较出二者的优劣。我们知道,二叉树有一个特点就是越往下节点越多。AdjustUp建堆时,节点少的层移动的多,节点多的层移动的少;而AdjustDown建堆时,节点多的层移动的少。节点少的层移动的多。
2.3 排序
堆建好之后就来到了排序。这里我们采用HeapPop的思想进行排序,其流程如下图:
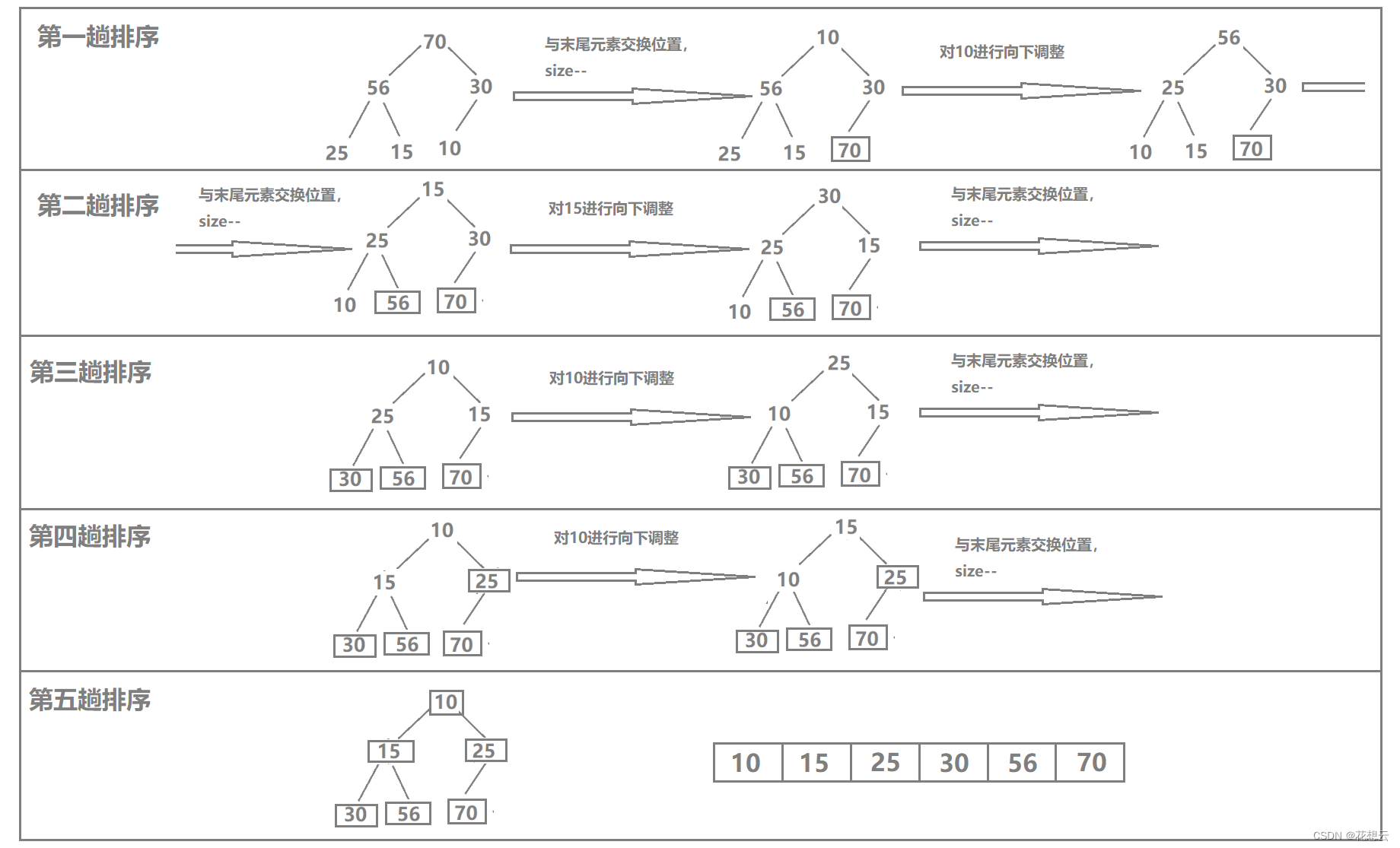
通过上图我们发现,当需要将数组排成升序时,就建大堆;当需要将数组排成降序时,就建小堆。
代码实现:
void HeapSort(int* a, int n)
{
//向上建堆
//for (int i = 0; i < n; i++)
//{
//AdjustUp(a, i);
//}
//向下建堆
for (int i = n - 1; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//升序建大堆,降序建小堆
//排序
int end = n-1;
while (end)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}此时排序的时间复杂度是可以估算的,堆的最后一层节点数是所有结点数的一半,同时,最后一层的节点所花费的步数最多。因为最坏情况下,最后一层的节点每一个都需要与堆顶交换,然后再向下调整到最后一层。所以,只看最后一次就可以估算出其时间复杂度为O(N*log N)。
3.堆排序的时间复杂度
堆排序的实现分为两个步骤:建堆与排序。
建堆我们选择最优的算法——AdjustDown,其时间复杂度为O(N);
排序的时间复杂度为O(N*log N);
因此,堆排序的时间复杂度为二者归并,即O(N*log N)。
相较于之前的冒泡排序、选择排序等O(N^2)量级的排序算法,堆排序已经比它们高出一个层次了,与举世闻名的快速排序进入同一等级。让我们期待一下飞速的快速排序是怎么做到比堆排序都更胜一筹的......
完整源码
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
//建大堆用'>',小堆用'<'
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void AdjustDown(HPDataType* a, int n, int parent)
{
assert(a);
//先默认较大的为左孩子
int child = parent * 2 + 1;
while (child < n)
{
//如果右孩子比左孩子大,就++
if (a[child] < a[child + 1] && child + 1 < n)
{
child++;
}
//建大堆用'>',小堆用'<'
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//向上建堆
//for (int i = 0; i < n; i++)
//{
//AdjustUp(a, i);
//}
//向下建堆
for (int i = n - 1; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//排序
int end = n-1;
while (end)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
void HeapSortTest()
{
int arr[] = { 12,34,45,78,56,74,3,7,9,5 };
//进行堆排序
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
//打印排序之后的数组
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
}
int main()
{
HeapSortTest();
return 0;
}