边界框回归(BBR)的损失函数对于目标检测至关重要。它的良好定义将为模型带来显著的性能改进。大多数现有的工作假设训练数据中的样本是高质量的,并侧重于增强BBR损失的拟合能力。
一、L2-norm
最初的基于回归的BBR损失定义为L2-norm,L2-norm损失主要有两个缺点:
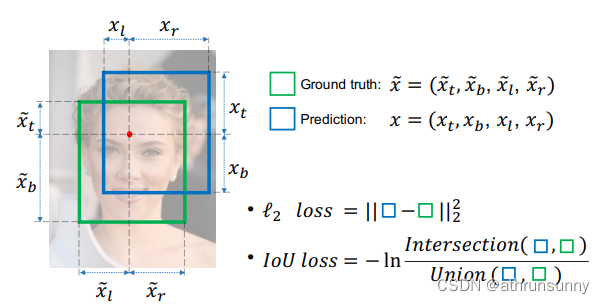
1、边界框的坐标(以xt、xb、xl、xr的形式)被优化为四个独立变量。这个假设违背了对象的边界高度相关的事实。简单的分开计算每个变量的回归loss无法反映这种相关性,它会导致预测框的一个或两个边界非常接近GT,但整个边界框是不满足条件的。
2、这种形式的损失函数并不能屏蔽边界框大小的干扰,使得模型对小目标的定位性能较差。
二、IoU loss
论文:《UnitBox: An Advanced Object Detection Network》
在目标检测任务中,使用IoU来测量anchor box与目标box之间的重叠程度。它以比例的形式有效地屏蔽了边界框大小的干扰,使该模型在使用1-IoU作为BBR损失时,能够很好地平衡对大物体和小物体的学习。
IoU loss的函数定义为:
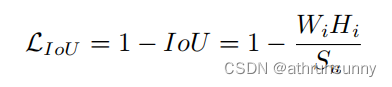
当边界框没有重叠时Liou对Wi求导会等于0,即:
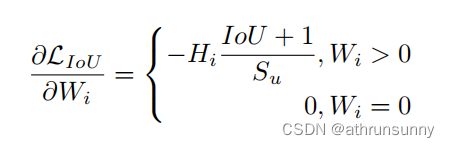
此时Liou的反向投影梯度消失,在训练期间无法更新重叠区域Wi的宽度。
IoU损失会有两个主要的缺点:
1、当预测框与真实框都没有交集时,计算出来的IoU都为0,损失都为1,但是缺失距离信息,预测框与GT相对位置较近时,损失函数应该较小。
2、当预测框和真实框的交并比相同,但是预测框所在位置不同,因为计算出来的损失一样,所以这样并不能判断哪种预测框更加准确。
现有的工作GIOU、DIOU、Focal EIOU、CIOU以及SIOU中考虑了许多与边界框相关的几何因子,并构造了惩罚项Ri来解决这个问题。现有的BBR损失遵循以下范例:
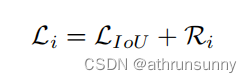
三、GIoU loss
论文:《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》
为了解决IoU loss的第一个问题,即当预测框与真实框都没有交集的时候,计算出来的IoU都为0,损失都为1,引入了一个最小闭包区的概念,即能将预测框和真实框包裹住的最小矩形框
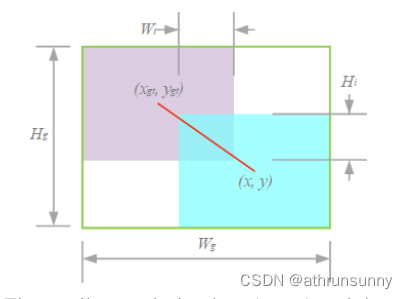
其中紫色框为GT,蓝色框为预测框,绿色的边框则为最小包围框。
GIoU的伪代码:

与IoU相似,GIoU也是一种距离度量,IoU取值[0,1],GIoU取值范围[-1,1]。在两者重合的时候取最大值1,在两者无交集且无限远的时候取最小值-1,因此GIoU是一个非常好的距离度量指标。与IoU只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度。
但是GIoU同时也存在一些问题:
1、当预测框包裹GT时,计算的iou相同,但是质量却不同,对于预测框的中心点靠近GT中心点的情况,loss应该相对小一些
GIoU loss的定义:

四、DIoU/CIoU loss
论文:《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》
DIoU为了解决GIoU中存在的问题,作者认为好的检测回归loss应该考虑三个几何度量,预测框和GT框的重叠度、中心点距离、长宽比的一致性。于是在IoU loss和GIoU loss基础上引入预测框和GT框中心点距离作DIoU loss,在DIoU loss基础上引入了预测框的长宽比和GT框的长宽比之间的差异作CIoU loss。此外,将DIoU加入nms替代IoU,提升了nms的鲁棒性。
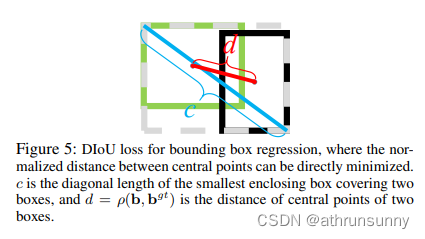
DIoU定义:
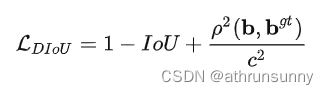
DIoU也存在一个缺点,当真实框和预测框的中心点重合时,但是长宽比不同,交并比一样,CIoU在此基础上增加一个惩罚项。
CIoU定义:
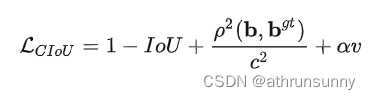
其中:

v用于计算预测框和目标框的高宽比的一致性,这里是用tan角来衡量
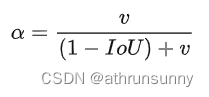
α是一个平衡参数(这个系数不参与梯度计算),这里根据IoU值来赋予优先级,当预测框和目标框IoU越大时,系数越大 。
五、EIoU Loss/Focal EIoU Loss
论文:Focal and Efficient IOU Loss for Accurate Bounding Box Regression》
主要思想:
一是认为CIoU loss对于长宽比加入loss的设计不太合理,于是将CIoU loss中反应长宽比一致性的部分替换成了分别对于长和宽的一致性loss,形成了EIoU loss。
二是认为不太好的回归样本对回归loss产生了比较大的影响,回归质量相对较好的样本则难以进一步优化,所以论文提出Focal EIoU loss进行回归质量较好和质量较差的样本之间的平衡。
EIoU loss定义:
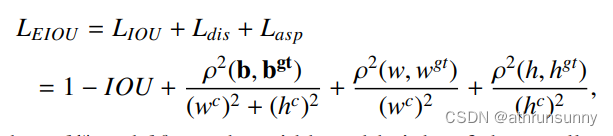
其中hc和wc为最小包围框的高和宽。
要平衡回归质量较好的样本的偏小loss和回归质量较差的样本的偏大loss,很自然的,选择和GT的IoU形成类似focal loss中的(1-p)的γ次方的权重来调节是一个很好的想法。
Focal EIoU loss定义:
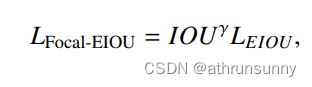
最终形式:
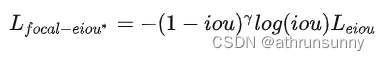
指标对比:

六、SIoU loss
论文:《SIoU Loss: More Powerful Learning for Bounding Box Regression》
已有方法匹配真实框和预测框之间的IoU、中心点距离、宽高比等,它们均未考虑真实框和预测框之间不匹配的方向。这种不足导致收敛速度较慢且效率较低,因为预测框可能在训练过程中“徘徊”,最终生成更差的模型。
本文提出了一种新的损失函数SCYLLA-IoU(SIoU),考虑到期望回归之间向量的角度,重新定义角度惩罚度量,它可以使预测框快速漂移到最近的轴,随后则只需要回归一个坐标(X或Y),这有效地减少了自由度的总数。
Zhora证明了中心对准anchor box具有更快的收敛速度,并根据角度成本、距离成本和形状成本构造了SIoU。

Angle cost描述了中心点连接(图1)与x-y轴之间的最小角度,当中心点在x轴或y轴上对齐时,Λ = 0。当中心点连接到x轴45°时,Λ = 1。这一惩罚可以引导anchor box移动到目标框的最近的轴上,减少了BBR的总自由度数。
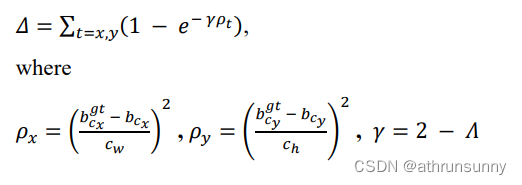
Distance cost描述了中心点之间的距离,其惩罚代价与角度代价呈正相关,当𝛼→0时,Distance cost的贡献大大降低。相反,𝛼越接近pi/4,Distance cost贡献越大。
具体来说:以X轴为例,即两框近乎平行时,a趋近于0,这样计算出来两框之间的角度距离接近于0,此时γ也接近于2,那么两框之间的距离对于整体loss的贡献变少了。而当a趋近与45°时,计算出来两框之间的角度为1,此时γ接近1,则两框之间的距离应该被重视,需要占更大的loss。
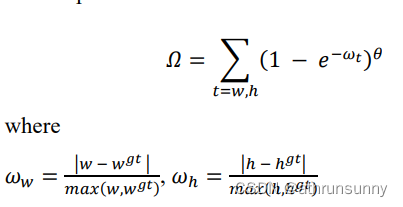
Shape cost这里作者考虑的两框之间的长宽比,是通过计算两框之间宽之差和二者之间最大宽之比(长同理)来定义的,大体思路和CIOU类似,只不过CIOU可以的考虑是两框整体形状的收敛,而SIoU是以长、宽两个边收敛来达到整体形状收敛的效果。
θ是个可调变量,来表示网络需要对形状这个,给予多少注意力,即占多少权重。实验中设置为4。
SIoU loss定义:
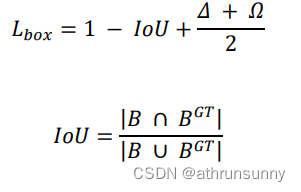
七、WIoU loss
论文:《Wise-IoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism》
Focal EIoU v1被提出来解决质量较好和质量较差的样本间的BBR平衡问题,但由于其静态聚焦机制(FM),非单调FM的潜力没有被充分利用,基于这一思想,作者提出了一种基于IoU的损失,该损失具有动态非单调FM,名为Wise IoU(WIoU)。
主要贡献总结如下:
-
提出了BBR的基于注意力的损失WIoU v1,它在仿真实验中实现了比最先进的SIoU更低的回归误差。
-
设计了具有单调FM的WIoU v2和具有动态非单调FM的WIoU v3。利用动态非单调FM的明智的梯度增益分配策略,WIoU v3获得了优越的性能。
-
对低质量的样本的影响进行了一系列详细的研究,证明了动态非单调调频的有效性和效率。
由于训练数据不可避免地包含低质量示例,几何因素(如距离和纵横比)将加重对低质量示例的惩罚,从而降低模型的泛化性能。当anchor box与目标盒很好地重合时,一个好的损失函数应该会削弱几何因素的惩罚,而较少的训练干预将使模型获得更好的泛化能力。
WIoU loss定义:

其中Wg,Hg表示最小包围框的宽和高。为了防止Rwiou产生阻碍收敛的梯度,Wg和Hg从计算图中分离出来(上标*表示此操作)。因为它有效地消除了阻碍收敛的因素,所以没有引入新的度量,例如纵横比。
1、Rwiou∈[1,e),这将显著放大普通质量anchor box的LIoU。
2、Liou∈[0,1],这将显著降低高质量anchor box的Rwiou,并在anchor box与目标框重合时,重点关注中心点之间的距离。
消融实验的结果:

代码
除WIoU外的其他IoU loss的实现可以参看我的另一篇文章:yolov5增加iou loss,无痛涨点trick