昇思25天学习打卡营第16天|Diffusion扩散模型，DCGAN生成漫画头像

Diffusion扩散模型

关于扩散模型（Diffusion Models）有很多种理解，本文的介绍是基于denoising diffusion probabilistic model （DDPM），DDPM已经在（无）条件图像/音频/视频生成领域取得了较多显著的成果，现有的比较受欢迎的的例子包括由OpenAI主导的GLIDE和DALL-E 2、由海德堡大学主导的潜在扩散和由Google Brain主导的图像生成。

实际上生成模型的扩散概念已经在（Sohl-Dickstein et al., 2015）中介绍过。然而，直到（Song et al., 2019）（斯坦福大学）和（Ho et al., 2020）（在Google Brain）才各自独立地改进了这种方法。

本文是在Phil Wang基于PyTorch框架的复现的基础上（而它本身又是基于TensorFlow实现），迁移到MindSpore AI框架上实现的。

import math
from functools import partial
%matplotlib inline
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
import numpy as np
from multiprocessing import cpu_count
from download import download

import mindspore as ms
import mindspore.nn as nn
import mindspore.ops as ops
from mindspore import Tensor, Parameter
from mindspore import dtype as mstype
from mindspore.dataset.vision import Resize, Inter, CenterCrop, ToTensor, RandomHorizontalFlip, ToPIL
from mindspore.common.initializer import initializer
from mindspore.amp import DynamicLossScaler

ms.set_seed(0)

模型简介

什么是Diffusion Model？

如果将Diffusion与其他生成模型（如Normalizing Flows、GAN或VAE）进行比较，它并没有那么复杂，它们都将噪声从一些简单分布转换为数据样本，Diffusion也是从纯噪声开始通过一个神经网络学习逐步去噪，最终得到一个实际图像。 Diffusion对于图像的处理包括以下两个过程：

我们选择的固定（或预定义）正向扩散过程 𝑞q ：它逐渐将高斯噪声添加到图像中，直到最终得到纯噪声
一个学习的反向去噪的扩散过程 𝑝𝜃pθ ：通过训练神经网络从纯噪声开始逐渐对图像去噪，直到最终得到一个实际的图像

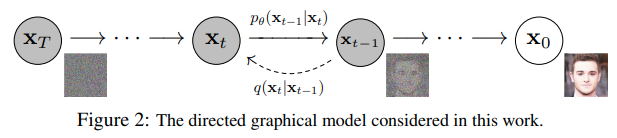
由 𝑡t 索引的正向和反向过程都发生在某些有限时间步长 𝑇（DDPM作者使用 𝑇=1000T=1000）内。从𝑡=0开始，在数据分布中采样真实图像 𝐱0（本文使用一张来自ImageNet的猫图像形象的展示了diffusion正向添加噪声的过程），正向过程在每个时间步长 𝑡 都从高斯分布中采样一些噪声，再添加到上一个时刻的图像中。假定给定一个足够大的 𝑇和一个在每个时间步长添加噪声的良好时间表，您最终会在 𝑡=𝑇 通过渐进的过程得到所谓的各向同性的高斯分布。

构建Diffusion模型

下面，我们逐步构建Diffusion模型。

首先，我们定义了一些帮助函数和类，这些函数和类将在实现神经网络时使用。

def rearrange(head, inputs):
    b, hc, x, y = inputs.shape
    c = hc // head
    return inputs.reshape((b, head, c, x * y))

def rsqrt(x):
    res = ops.sqrt(x)
    return ops.inv(res)

def randn_like(x, dtype=None):
    if dtype is None:
        dtype = x.dtype
    res = ops.standard_normal(x.shape).astype(dtype)
    return res

def randn(shape, dtype=None):
    if dtype is None:
        dtype = ms.float32
    res = ops.standard_normal(shape).astype(dtype)
    return res

def randint(low, high, size, dtype=ms.int32):
    res = ops.uniform(size, Tensor(low, dtype), Tensor(high, dtype), dtype=dtype)
    return res

def exists(x):
    return x is not None

def default(val, d):
    if exists(val):
        return val
    return d() if callable(d) else d

def _check_dtype(d1, d2):
    if ms.float32 in (d1, d2):
        return ms.float32
    if d1 == d2:
        return d1
    raise ValueError('dtype is not supported.')

class Residual(nn.Cell):
    def __init__(self, fn):
        super().__init__()
        self.fn = fn

    def construct(self, x, *args, **kwargs):
        return self.fn(x, *args, **kwargs) + x

def Upsample(dim):
    return nn.Conv2dTranspose(dim, dim, 4, 2, pad_mode="pad", padding=1)

def Downsample(dim):
    return nn.Conv2d(dim, dim, 4, 2, pad_mode="pad", padding=1)

位置向量

由于神经网络的参数在时间（噪声水平）上共享，作者使用正弦位置嵌入来编码𝑡t，灵感来自Transformer（Vaswani et al., 2017）。对于批处理中的每一张图像，神经网络"知道"它在哪个特定时间步长（噪声水平）上运行。

SinusoidalPositionEmbeddings模块采用(batch_size, 1)形状的张量作为输入（即批处理中几个有噪声图像的噪声水平），并将其转换为(batch_size, dim)形状的张量，其中dim是位置嵌入的尺寸。然后，我们将其添加到每个剩余块中。

class SinusoidalPositionEmbeddings(nn.Cell):
    def __init__(self, dim):
        super().__init__()
        self.dim = dim
        half_dim = self.dim // 2
        emb = math.log(10000) / (half_dim - 1)
        emb = np.exp(np.arange(half_dim) * - emb)
        self.emb = Tensor(emb, ms.float32)

    def construct(self, x):
        emb = x[:, None] * self.emb[None, :]
        emb = ops.concat((ops.sin(emb), ops.cos(emb)), axis=-1)
        return emb

ResNet/ConvNeXT块

接下来，我们定义U-Net模型的核心构建块。DDPM作者使用了一个Wide ResNet块（Zagoruyko et al., 2016），但Phil Wang决定添加ConvNeXT（Liu et al., 2022）替换ResNet，因为后者在图像领域取得了巨大成功。

在最终的U-Net架构中，可以选择其中一个或另一个，本文选择ConvNeXT块构建U-Net模型。

class Block(nn.Cell):
    def __init__(self, dim, dim_out, groups=1):
        super().__init__()
        self.proj = nn.Conv2d(dim, dim_out, 3, pad_mode="pad", padding=1)
        self.proj = c(dim, dim_out, 3, padding=1, pad_mode='pad')
        self.norm = nn.GroupNorm(groups, dim_out)
        self.act = nn.SiLU()

    def construct(self, x, scale_shift=None):
        x = self.proj(x)
        x = self.norm(x)

        if exists(scale_shift):
            scale, shift = scale_shift
            x = x * (scale + 1) + shift

        x = self.act(x)
        return x

class ConvNextBlock(nn.Cell):
    def __init__(self, dim, dim_out, *, time_emb_dim=None, mult=2, norm=True):
        super().__init__()
        self.mlp = (
            nn.SequentialCell(nn.GELU(), nn.Dense(time_emb_dim, dim))
            if exists(time_emb_dim)
            else None
        )

        self.ds_conv = nn.Conv2d(dim, dim, 7, padding=3, group=dim, pad_mode="pad")
        self.net = nn.SequentialCell(
            nn.GroupNorm(1, dim) if norm else nn.Identity(),
            nn.Conv2d(dim, dim_out * mult, 3, padding=1, pad_mode="pad"),
            nn.GELU(),
            nn.GroupNorm(1, dim_out * mult),
            nn.Conv2d(dim_out * mult, dim_out, 3, padding=1, pad_mode="pad"),
        )

        self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()

    def construct(self, x, time_emb=None):
        h = self.ds_conv(x)
        if exists(self.mlp) and exists(time_emb):
            assert exists(time_emb), "time embedding must be passed in"
            condition = self.mlp(time_emb)
            condition = condition.expand_dims(-1).expand_dims(-1)
            h = h + condition

        h = self.net(h)
        return h + self.res_conv(x)

Attention模块

接下来，我们定义Attention模块，DDPM作者将其添加到卷积块之间。Attention是著名的Transformer架构(Vaswani et al., 2017)，在人工智能的各个领域都取得了巨大的成功，从NLP到蛋白质折叠。Phil Wang使用了两种注意力变体：一种是常规的multi-head self-attention（如Transformer中使用的），另一种是LinearAttention(Shen et al., 2018)，其时间和内存要求在序列长度上线性缩放，而不是在常规注意力中缩放。要想对Attention机制进行深入的了解，请参照Jay Allamar的精彩的博文。

class Attention(nn.Cell):
    def __init__(self, dim, heads=4, dim_head=32):
        super().__init__()
        self.scale = dim_head ** -0.5
        self.heads = heads
        hidden_dim = dim_head * heads

        self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, pad_mode='valid', has_bias=False)
        self.to_out = nn.Conv2d(hidden_dim, dim, 1, pad_mode='valid', has_bias=True)
        self.map = ops.Map()
        self.partial = ops.Partial()

    def construct(self, x):
        b, _, h, w = x.shape
        qkv = self.to_qkv(x).chunk(3, 1)
        q, k, v = self.map(self.partial(rearrange, self.heads), qkv)

        q = q * self.scale

        # 'b h d i, b h d j -> b h i j'
        sim = ops.bmm(q.swapaxes(2, 3), k)
        attn = ops.softmax(sim, axis=-1)
        # 'b h i j, b h d j -> b h i d'
        out = ops.bmm(attn, v.swapaxes(2, 3))
        out = out.swapaxes(-1, -2).reshape((b, -1, h, w))

        return self.to_out(out)


class LayerNorm(nn.Cell):
    def __init__(self, dim):
        super().__init__()
        self.g = Parameter(initializer('ones', (1, dim, 1, 1)), name='g')

    def construct(self, x):
        eps = 1e-5
        var = x.var(1, keepdims=True)
        mean = x.mean(1, keep_dims=True)
        return (x - mean) * rsqrt((var + eps)) * self.g


class LinearAttention(nn.Cell):
    def __init__(self, dim, heads=4, dim_head=32):
        super().__init__()
        self.scale = dim_head ** -0.5
        self.heads = heads
        hidden_dim = dim_head * heads
        self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, pad_mode='valid', has_bias=False)

        self.to_out = nn.SequentialCell(
            nn.Conv2d(hidden_dim, dim, 1, pad_mode='valid', has_bias=True),
            LayerNorm(dim)
        )

        self.map = ops.Map()
        self.partial = ops.Partial()

    def construct(self, x):
        b, _, h, w = x.shape
        qkv = self.to_qkv(x).chunk(3, 1)
        q, k, v = self.map(self.partial(rearrange, self.heads), qkv)

        q = ops.softmax(q, -2)
        k = ops.softmax(k, -1)

        q = q * self.scale
        v = v / (h * w)

        # 'b h d n, b h e n -> b h d e'
        context = ops.bmm(k, v.swapaxes(2, 3))
        # 'b h d e, b h d n -> b h e n'
        out = ops.bmm(context.swapaxes(2, 3), q)

        out = out.reshape((b, -1, h, w))
        return self.to_out(out)

组归一化

DDPM作者将U-Net的卷积/注意层与群归一化（Wu et al., 2018）。下面，我们定义一个PreNorm类，将用于在注意层之前应用groupnorm。

class PreNorm(nn.Cell):
    def __init__(self, dim, fn):
        super().__init__()
        self.fn = fn
        self.norm = nn.GroupNorm(1, dim)

    def construct(self, x):
        x = self.norm(x)
        return self.fn(x)

条件U-Net

我们已经定义了所有的构建块（位置嵌入、ResNet/ConvNeXT块、Attention和组归一化），现在需要定义整个神经网络了。请记住，网络 𝜖𝜃(𝐱𝑡,𝑡)ϵθ(xt,t) 的工作是接收一批噪声图像+噪声水平，并输出添加到输入中的噪声。

更具体的：网络获取了一批(batch_size, num_channels, height, width)形状的噪声图像和一批(batch_size, 1)形状的噪音水平作为输入，并返回(batch_size, num_channels, height, width)形状的张量。

网络构建过程如下：

首先，将卷积层应用于噪声图像批上，并计算噪声水平的位置
接下来，应用一系列下采样级。每个下采样阶段由2个ResNet/ConvNeXT块 + groupnorm + attention + 残差连接 + 一个下采样操作组成
在网络的中间，再次应用ResNet或ConvNeXT块，并与attention交织
接下来，应用一系列上采样级。每个上采样级由2个ResNet/ConvNeXT块+ groupnorm + attention + 残差连接 + 一个上采样操作组成
最后，应用ResNet/ConvNeXT块，然后应用卷积层

最终，神经网络将层堆叠起来，就像它们是乐高积木一样（但重要的是了解它们是如何工作的）

class Unet(nn.Cell):
    def __init__(
            self,
            dim,
            init_dim=None,
            out_dim=None,
            dim_mults=(1, 2, 4, 8),
            channels=3,
            with_time_emb=True,
            convnext_mult=2,
    ):
        super().__init__()

        self.channels = channels

        init_dim = default(init_dim, dim // 3 * 2)
        self.init_conv = nn.Conv2d(channels, init_dim, 7, padding=3, pad_mode="pad", has_bias=True)

        dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
        in_out = list(zip(dims[:-1], dims[1:]))

        block_klass = partial(ConvNextBlock, mult=convnext_mult)

        if with_time_emb:
            time_dim = dim * 4
            self.time_mlp = nn.SequentialCell(
                SinusoidalPositionEmbeddings(dim),
                nn.Dense(dim, time_dim),
                nn.GELU(),
                nn.Dense(time_dim, time_dim),
            )
        else:
            time_dim = None
            self.time_mlp = None

        self.downs = nn.CellList([])
        self.ups = nn.CellList([])
        num_resolutions = len(in_out)

        for ind, (dim_in, dim_out) in enumerate(in_out):
            is_last = ind >= (num_resolutions - 1)

            self.downs.append(
                nn.CellList(
                    [
                        block_klass(dim_in, dim_out, time_emb_dim=time_dim),
                        block_klass(dim_out, dim_out, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_out, LinearAttention(dim_out))),
                        Downsample(dim_out) if not is_last else nn.Identity(),
                    ]
                )
            )

        mid_dim = dims[-1]
        self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
        self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
        self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)

        for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])):
            is_last = ind >= (num_resolutions - 1)

            self.ups.append(
                nn.CellList(
                    [
                        block_klass(dim_out * 2, dim_in, time_emb_dim=time_dim),
                        block_klass(dim_in, dim_in, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_in, LinearAttention(dim_in))),
                        Upsample(dim_in) if not is_last else nn.Identity(),
                    ]
                )
            )

        out_dim = default(out_dim, channels)
        self.final_conv = nn.SequentialCell(
            block_klass(dim, dim), nn.Conv2d(dim, out_dim, 1)
        )

    def construct(self, x, time):
        x = self.init_conv(x)

        t = self.time_mlp(time) if exists(self.time_mlp) else None

        h = []

        for block1, block2, attn, downsample in self.downs:
            x = block1(x, t)
            x = block2(x, t)
            x = attn(x)
            h.append(x)

            x = downsample(x)

        x = self.mid_block1(x, t)
        x = self.mid_attn(x)
        x = self.mid_block2(x, t)

        len_h = len(h) - 1
        for block1, block2, attn, upsample in self.ups:
            x = ops.concat((x, h[len_h]), 1)
            len_h -= 1
            x = block1(x, t)
            x = block2(x, t)
            x = attn(x)

            x = upsample(x)
        return self.final_conv(x)

正向扩散

我们已经知道正向扩散过程在多个时间步长𝑇T中，从实际分布逐渐向图像添加噪声，根据差异计划进行正向扩散。最初的DDPM作者采用了线性时间表：

我们将正向过程方差设置为常数，从𝛽1=10−4β1=10−4线性增加到𝛽𝑇=0.02βT=0.02。
但是，它在（Nichol et al., 2021）中表明，当使用余弦调度时，可以获得更好的结果。

下面，我们定义了𝑇T时间步的时间表。

def linear_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return np.linspace(beta_start, beta_end, timesteps).astype(np.float32)

首先，让我们使用T=200 时间步长的线性计划，并定义我们需要的 βt 中的各种变量，例如方差 α¯t 的累积乘积。下面的每个变量都只是一维张量，存储从 t 到 T 的值。重要的是，我们还定义了extract函数，它将允许我们提取一批适当的 t 索引。

# 扩散200步
timesteps = 200

# 定义 beta schedule
betas = linear_beta_schedule(timesteps=timesteps)

# 定义 alphas
alphas = 1. - betas
alphas_cumprod = np.cumprod(alphas, axis=0)
alphas_cumprod_prev = np.pad(alphas_cumprod[:-1], (1, 0), constant_values=1)

sqrt_recip_alphas = Tensor(np.sqrt(1. / alphas))
sqrt_alphas_cumprod = Tensor(np.sqrt(alphas_cumprod))
sqrt_one_minus_alphas_cumprod = Tensor(np.sqrt(1. - alphas_cumprod))

# 计算 q(x_{t-1} | x_t, x_0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)

p2_loss_weight = (1 + alphas_cumprod / (1 - alphas_cumprod)) ** -0.
p2_loss_weight = Tensor(p2_loss_weight)

def extract(a, t, x_shape):
    b = t.shape[0]
    out = Tensor(a).gather(t, -1)
    return out.reshape(b, *((1,) * (len(x_shape) - 1)))

# 下载猫猫图像
url = 'https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/datasets/image_cat.zip'
path = download(url, './', kind="zip", replace=True)

from PIL import Image

image = Image.open('./image_cat/jpg/000000039769.jpg')
base_width = 160
image = image.resize((base_width, int(float(image.size[1]) * float(base_width / float(image.size[0])))))
image.show()

噪声被添加到mindspore张量中，而不是Pillow图像。我们将首先定义图像转换，允许我们从PIL图像转换到mindspore张量（我们可以在其上添加噪声），反之亦然。

这些转换相当简单：我们首先通过除以255来标准化图像（使它们在 [0,1]范围内），然后确保它们在 [−1,1]范围内。DPPM论文中有介绍到：

假设图像数据由 {0,1,...,255} 中的整数组成，线性缩放为 [−1,1]，这确保了神经网络反向过程在从标准正常先验 𝑝(𝐱𝑇)开始的一致缩放输入上运行。

from mindspore.dataset import ImageFolderDataset

image_size = 128
transforms = [
    Resize(image_size, Inter.BILINEAR),
    CenterCrop(image_size),
    ToTensor(),
    lambda t: (t * 2) - 1
]


path = './image_cat'
dataset = ImageFolderDataset(dataset_dir=path, num_parallel_workers=cpu_count(),
                             extensions=['.jpg', '.jpeg', '.png', '.tiff'],
                             num_shards=1, shard_id=0, shuffle=False, decode=True)
dataset = dataset.project('image')
transforms.insert(1, RandomHorizontalFlip())
dataset_1 = dataset.map(transforms, 'image')
dataset_2 = dataset_1.batch(1, drop_remainder=True)
x_start = next(dataset_2.create_tuple_iterator())[0]
print(x_start.shape)

我们还定义了反向变换，它接收一个包含 [−1,1][−1,1] 中的张量，并将它们转回 PIL 图像：

import numpy as np

reverse_transform = [
    lambda t: (t + 1) / 2,
    lambda t: ops.permute(t, (1, 2, 0)), # CHW to HWC
    lambda t: t * 255.,
    lambda t: t.asnumpy().astype(np.uint8),
    ToPIL()
]

def compose(transform, x):
    for d in transform:
        x = d(x)
    return x

让我们验证一下：

reverse_image = compose(reverse_transform, x_start[0])
reverse_image.show()

我们现在可以定义前向扩散过程，如本文所示：

def q_sample(x_start, t, noise=None):
    if noise is None:
        noise = randn_like(x_start)
    return (extract(sqrt_alphas_cumprod, t, x_start.shape) * x_start +
            extract(sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise)

让我们在特定的时间步长上测试它：

def get_noisy_image(x_start, t):
    # 添加噪音
    x_noisy = q_sample(x_start, t=t)

    # 转换为 PIL 图像
    noisy_image = compose(reverse_transform, x_noisy[0])

    return noisy_image

# 设置 time step
t = Tensor([40])
noisy_image = get_noisy_image(x_start, t)
print(noisy_image)
noisy_image.show()

让我们为不同的时间步骤可视化此情况：

import matplotlib.pyplot as plt

def plot(imgs, with_orig=False, row_title=None, **imshow_kwargs):
    if not isinstance(imgs[0], list):
        imgs = [imgs]

    num_rows = len(imgs)
    num_cols = len(imgs[0]) + with_orig
    _, axs = plt.subplots(figsize=(200, 200), nrows=num_rows, ncols=num_cols, squeeze=False)
    for row_idx, row in enumerate(imgs):
        row = [image] + row if with_orig else row
        for col_idx, img in enumerate(row):
            ax = axs[row_idx, col_idx]
            ax.imshow(np.asarray(img), **imshow_kwargs)
            ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])

    if with_orig:
        axs[0, 0].set(title='Original image')
        axs[0, 0].title.set_size(8)
    if row_title is not None:
        for row_idx in range(num_rows):
            axs[row_idx, 0].set(ylabel=row_title[row_idx])

    plt.tight_layout()

plot([get_noisy_image(x_start, Tensor([t])) for t in [0, 50, 100, 150, 199]])

这意味着我们现在可以定义给定模型的损失函数，如下所示：

def p_losses(unet_model, x_start, t, noise=None):
    if noise is None:
        noise = randn_like(x_start)
    x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
    predicted_noise = unet_model(x_noisy, t)

    loss = nn.SmoothL1Loss()(noise, predicted_noise)# todo
    loss = loss.reshape(loss.shape[0], -1)
    loss = loss * extract(p2_loss_weight, t, loss.shape)
    return loss.mean()

denoise_model将是我们上面定义的U-Net。我们将在真实噪声和预测噪声之间使用Huber损失。

数据准备与处理

在这里我们定义一个正则数据集。数据集可以来自简单的真实数据集的图像组成，如Fashion-MNIST、CIFAR-10或ImageNet，其中线性缩放为 [−1,1]。

每个图像的大小都会调整为相同的大小。有趣的是，图像也是随机水平翻转的。根据论文内容：我们在CIFAR10的训练中使用了随机水平翻转；我们尝试了有翻转和没有翻转的训练，并发现翻转可以稍微提高样本质量。

本实验我们选用Fashion_MNIST数据集，我们使用download下载并解压Fashion_MNIST数据集到指定路径。此数据集由已经具有相同分辨率的图像组成，即28x28。

# 下载MNIST数据集
url = 'https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/datasets/dataset.zip'
path = download(url, './', kind="zip", replace=True)

from mindspore.dataset import FashionMnistDataset

image_size = 28
channels = 1
batch_size = 16

fashion_mnist_dataset_dir = "./dataset"
dataset = FashionMnistDataset(dataset_dir=fashion_mnist_dataset_dir, usage="train", num_parallel_workers=cpu_count(), shuffle=True, num_shards=1, shard_id=0)

接下来，我们定义一个transform操作，将在整个数据集上动态应用该操作。该操作应用一些基本的图像预处理：随机水平翻转、重新调整，最后使它们的值在 [−1,1]范围内。

transforms = [
    RandomHorizontalFlip(),
    ToTensor(),
    lambda t: (t * 2) - 1
]


dataset = dataset.project('image')
dataset = dataset.shuffle(64)
dataset = dataset.map(transforms, 'image')
dataset = dataset.batch(16, drop_remainder=True)

x = next(dataset.create_dict_iterator())
print(x.keys())

采样

由于我们将在训练期间从模型中采样（以便跟踪进度），我们定义了下面的代码。采样在本文中总结为算法2：

从扩散模型生成新图像是通过反转扩散过程来实现的：我们从𝑇T开始，我们从高斯分布中采样纯噪声，然后使用我们的神经网络逐渐去噪（使用它所学习的条件概率），直到我们最终在时间步𝑡=0结束。如上图所示，我们可以通过使用我们的噪声预测器插入平均值的重新参数化，导出一个降噪程度较低的图像 𝐱𝑡−1xt−1。请注意，方差是提前知道的。

理想情况下，我们最终会得到一个看起来像是来自真实数据分布的图像。

下面的代码实现了这一点。

def p_sample(model, x, t, t_index):
    betas_t = extract(betas, t, x.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x.shape
    )
    sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
    model_mean = sqrt_recip_alphas_t * (x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t)

    if t_index == 0:
        return model_mean
    posterior_variance_t = extract(posterior_variance, t, x.shape)
    noise = randn_like(x)
    return model_mean + ops.sqrt(posterior_variance_t) * noise

def p_sample_loop(model, shape):
    b = shape[0]
    # 从纯噪声开始
    img = randn(shape, dtype=None)
    imgs = []

    for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
        img = p_sample(model, img, ms.numpy.full((b,), i, dtype=mstype.int32), i)
        imgs.append(img.asnumpy())
    return imgs

def sample(model, image_size, batch_size=16, channels=3):
    return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))

请注意，上面的代码是原始实现的简化版本。

训练过程

下面，我们开始训练吧！

# 定义动态学习率
lr = nn.cosine_decay_lr(min_lr=1e-7, max_lr=1e-4, total_step=10*3750, step_per_epoch=3750, decay_epoch=10)

# 定义 Unet模型
unet_model = Unet(
    dim=image_size,
    channels=channels,
    dim_mults=(1, 2, 4,)
)

name_list = []
for (name, par) in list(unet_model.parameters_and_names()):
    name_list.append(name)
i = 0
for item in list(unet_model.trainable_params()):
    item.name = name_list[i]
    i += 1

# 定义优化器
optimizer = nn.Adam(unet_model.trainable_params(), learning_rate=lr)
loss_scaler = DynamicLossScaler(65536, 2, 1000)

# 定义前向过程
def forward_fn(data, t, noise=None):
    loss = p_losses(unet_model, data, t, noise)
    return loss

# 计算梯度
grad_fn = ms.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=False)

# 梯度更新
def train_step(data, t, noise):
    loss, grads = grad_fn(data, t, noise)
    optimizer(grads)
    return loss

import time

# 由于时间原因，epochs设置为1，可根据需求进行调整
epochs = 1

for epoch in range(epochs):
    begin_time = time.time()
    for step, batch in enumerate(dataset.create_tuple_iterator()):
        unet_model.set_train()
        batch_size = batch[0].shape[0]
        t = randint(0, timesteps, (batch_size,), dtype=ms.int32)
        noise = randn_like(batch[0])
        loss = train_step(batch[0], t, noise)

        if step % 500 == 0:
            print(" epoch: ", epoch, " step: ", step, " Loss: ", loss)
    end_time = time.time()
    times = end_time - begin_time
    print("training time:", times, "s")
    # 展示随机采样效果
    unet_model.set_train(False)
    samples = sample(unet_model, image_size=image_size, batch_size=64, channels=channels)
    plt.imshow(samples[-1][5].reshape(image_size, image_size, channels), cmap="gray")
print("Training Success!")

推理过程（从模型中采样）

要从模型中采样，我们可以只使用上面定义的采样函数：

# 采样64个图片
unet_model.set_train(False)
samples = sample(unet_model, image_size=image_size, batch_size=64, channels=channels)

# 展示一个随机效果
random_index = 5
plt.imshow(samples[-1][random_index].reshape(image_size, image_size, channels), cmap="gray")

可以看到这个模型能产生一件衣服！

请注意，我们训练的数据集分辨率相当低（28x28）。

我们还可以创建去噪过程的gif：

import matplotlib.animation as animation

random_index = 53

fig = plt.figure()
ims = []
for i in range(timesteps):
    im = plt.imshow(samples[i][random_index].reshape(image_size, image_size, channels), cmap="gray", animated=True)
    ims.append([im])

animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=100)
animate.save('diffusion.gif')
plt.show()

总结

请注意，DDPM论文表明扩散模型是（非）条件图像有希望生成的方向。自那以后，diffusion得到了（极大的）改进，最明显的是文本条件图像生成。下面，我们列出了一些重要的（但远非详尽无遗的）后续工作：

改进的去噪扩散概率模型(Nichol et al., 2021)：发现学习条件分布的方差（除平均值外）有助于提高性能
用于高保真图像生成的级联扩散模型([Ho et al., 2021)：引入级联扩散，它包括多个扩散模型的流水线，这些模型生成分辨率提高的图像，用于高保真图像合成
扩散模型在图像合成上击败了GANs(Dhariwal et al., 2021)：表明扩散模型通过改进U-Net体系结构以及引入分类器指导，可以获得优于当前最先进的生成模型的图像样本质量
无分类器扩散指南([Ho et al., 2021)：表明通过使用单个神经网络联合训练条件和无条件扩散模型，不需要分类器来指导扩散模型
具有CLIP Latents (DALL-E 2) 的分层文本条件图像生成 (Ramesh et al., 2022)：在将文本标题转换为CLIP图像嵌入之前使用，然后扩散模型将其解码为图像
具有深度语言理解的真实文本到图像扩散模型（ImageGen）(Saharia et al., 2022)：表明将大型预训练语言模型（例如T5）与级联扩散结合起来，对于文本到图像的合成很有效

请注意，此列表仅包括在撰写本文，即2022年6月7日之前的重要作品。

目前，扩散模型的主要（也许唯一）缺点是它们需要多次正向传递来生成图像（对于像GAN这样的生成模型来说，情况并非如此）。然而，有正在进行中的研究表明只需要10个去噪步骤就能实现高保真生成。

最后打卡今天的学习时间

心得

通过今天的学习我对Diffusion扩散模型有了更深入的了解。扩散模型在机器学习领域中扮演着重要角色，尤其在图像生成和风格迁移中展现出其独特的魅力。通过学习，我认识到了扩散过程的基本原理，以及如何利用这一过程来生成高质量的图像。这种模型的创新之处在于它能够模拟数据的生成过程，从而在保持多样性的同时，生成更加逼真的结果。我期待将这些知识应用到实际项目中，以解决更复杂的问题

DCGAN生成漫画头像

GAN基础原理

这部分原理介绍参考GAN图像生成。

DCGAN原理

DCGAN（深度卷积对抗生成网络，Deep Convolutional Generative Adversarial Networks）是GAN的直接扩展。不同之处在于，DCGAN会分别在判别器和生成器中使用卷积和转置卷积层。

它最早由Radford等人在论文Unsupervised Representation Learning With Deep Convolutional Generative Adversarial Networks中进行描述。判别器由分层的卷积层、BatchNorm层和LeakyReLU激活层组成。输入是3x64x64的图像，输出是该图像为真图像的概率。生成器则是由转置卷积层、BatchNorm层和ReLU激活层组成。输入是标准正态分布中提取出的隐向量𝑧z，输出是3x64x64的RGB图像。

本教程将使用动漫头像数据集来训练一个生成式对抗网络，接着使用该网络生成动漫头像图片。

数据准备与处理

首先我们将数据集下载到指定目录下并解压。示例代码如下：

%%capture captured_output
# 实验环境已经预装了mindspore==2.2.14，如需更换mindspore版本，可更改下面mindspore的版本号
!pip uninstall mindspore -y
!pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspore==2.2.14

from download import download

url = "https://download.mindspore.cn/dataset/Faces/faces.zip"

path = download(url, "./faces", kind="zip", replace=True)

数据处理

首先为执行过程定义一些输入：

batch_size = 128          # 批量大小
image_size = 64           # 训练图像空间大小
nc = 3                    # 图像彩色通道数
nz = 100                  # 隐向量的长度
ngf = 64                  # 特征图在生成器中的大小
ndf = 64                  # 特征图在判别器中的大小
num_epochs = 3           # 训练周期数
lr = 0.0002               # 学习率
beta1 = 0.5               # Adam优化器的beta1超参数

定义create_dataset_imagenet函数对数据进行处理和增强操作。

import numpy as np
import mindspore.dataset as ds
import mindspore.dataset.vision as vision

def create_dataset_imagenet(dataset_path):
    """数据加载"""
    dataset = ds.ImageFolderDataset(dataset_path,
                                    num_parallel_workers=4,
                                    shuffle=True,
                                    decode=True)

    # 数据增强操作
    transforms = [
        vision.Resize(image_size),
        vision.CenterCrop(image_size),
        vision.HWC2CHW(),
        lambda x: ((x / 255).astype("float32"))
    ]

    # 数据映射操作
    dataset = dataset.project('image')
    dataset = dataset.map(transforms, 'image')

    # 批量操作
    dataset = dataset.batch(batch_size)
    return dataset

dataset = create_dataset_imagenet('./faces')

通过create_dict_iterator函数将数据转换成字典迭代器，然后使用matplotlib模块可视化部分训练数据。

import matplotlib.pyplot as plt

def plot_data(data):
    # 可视化部分训练数据
    plt.figure(figsize=(10, 3), dpi=140)
    for i, image in enumerate(data[0][:30], 1):
        plt.subplot(3, 10, i)
        plt.axis("off")
        plt.imshow(image.transpose(1, 2, 0))
    plt.show()

sample_data = next(dataset.create_tuple_iterator(output_numpy=True))
plot_data(sample_data)

构造网络

当处理完数据后，就可以来进行网络的搭建了。按照DCGAN论文中的描述，所有模型权重均应从mean为0，sigma为0.02的正态分布中随机初始化。

生成器

生成器G的功能是将隐向量z映射到数据空间。由于数据是图像，这一过程也会创建与真实图像大小相同的 RGB 图像。在实践场景中，该功能是通过一系列Conv2dTranspose转置卷积层来完成的，每个层都与BatchNorm2d层和ReLu激活层配对，输出数据会经过tanh函数，使其返回[-1,1]的数据范围内。

DCGAN论文生成图像如下所示：

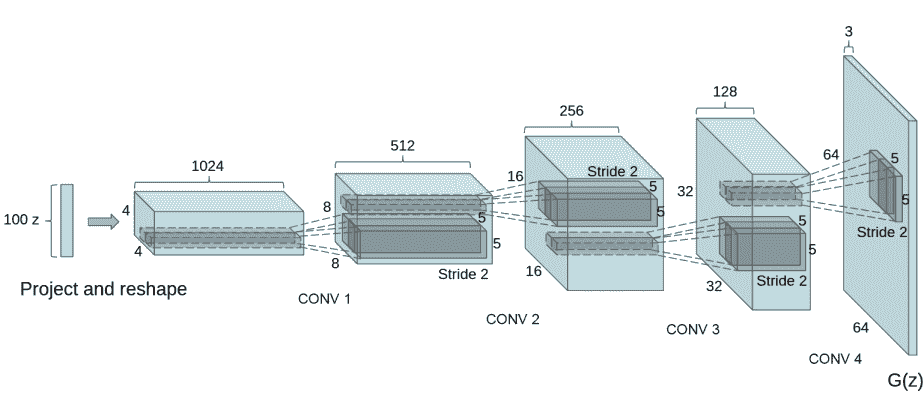
dcgangenerator

图片来源：Unsupervised Representation Learning With Deep Convolutional Generative Adversarial Networks.

我们通过输入部分中设置的nz、ngf和nc来影响代码中的生成器结构。nz是隐向量z的长度，ngf与通过生成器传播的特征图的大小有关，nc是输出图像中的通道数。

以下是生成器的代码实现：

import mindspore as ms
from mindspore import nn, ops
from mindspore.common.initializer import Normal

weight_init = Normal(mean=0, sigma=0.02)
gamma_init = Normal(mean=1, sigma=0.02)

class Generator(nn.Cell):
    """DCGAN网络生成器"""

    def __init__(self):
        super(Generator, self).__init__()
        self.generator = nn.SequentialCell(
            nn.Conv2dTranspose(nz, ngf * 8, 4, 1, 'valid', weight_init=weight_init),
            nn.BatchNorm2d(ngf * 8, gamma_init=gamma_init),
            nn.ReLU(),
            nn.Conv2dTranspose(ngf * 8, ngf * 4, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.BatchNorm2d(ngf * 4, gamma_init=gamma_init),
            nn.ReLU(),
            nn.Conv2dTranspose(ngf * 4, ngf * 2, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.BatchNorm2d(ngf * 2, gamma_init=gamma_init),
            nn.ReLU(),
            nn.Conv2dTranspose(ngf * 2, ngf, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.BatchNorm2d(ngf, gamma_init=gamma_init),
            nn.ReLU(),
            nn.Conv2dTranspose(ngf, nc, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.Tanh()
            )

    def construct(self, x):
        return self.generator(x)

generator = Generator()

判别器¶

如前所述，判别器D是一个二分类网络模型，输出判定该图像为真实图的概率。通过一系列的Conv2d、BatchNorm2d和LeakyReLU层对其进行处理，最后通过Sigmoid激活函数得到最终概率。

DCGAN论文提到，使用卷积而不是通过池化来进行下采样是一个好方法，因为它可以让网络学习自己的池化特征。

判别器的代码实现如下：

class Discriminator(nn.Cell):
    """DCGAN网络判别器"""

    def __init__(self):
        super(Discriminator, self).__init__()
        self.discriminator = nn.SequentialCell(
            nn.Conv2d(nc, ndf, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.LeakyReLU(0.2),
            nn.Conv2d(ndf, ndf * 2, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.BatchNorm2d(ngf * 2, gamma_init=gamma_init),
            nn.LeakyReLU(0.2),
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.BatchNorm2d(ngf * 4, gamma_init=gamma_init),
            nn.LeakyReLU(0.2),
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 'pad', 1, weight_init=weight_init),
            nn.BatchNorm2d(ngf * 8, gamma_init=gamma_init),
            nn.LeakyReLU(0.2),
            nn.Conv2d(ndf * 8, 1, 4, 1, 'valid', weight_init=weight_init),
            )
        self.adv_layer = nn.Sigmoid()

    def construct(self, x):
        out = self.discriminator(x)
        out = out.reshape(out.shape[0], -1)
        return self.adv_layer(out)

discriminator = Discriminator()

模型训练

损失函数

当定义了D和G后，接下来将使用MindSpore中定义的二进制交叉熵损失函数BCELoss。

# 定义损失函数
adversarial_loss = nn.BCELoss(reduction='mean')

优化器

这里设置了两个单独的优化器，一个用于D，另一个用于G。这两个都是lr = 0.0002和beta1 = 0.5的Adam优化器。

# 为生成器和判别器设置优化器
optimizer_D = nn.Adam(discriminator.trainable_params(), learning_rate=lr, beta1=beta1)
optimizer_G = nn.Adam(generator.trainable_params(), learning_rate=lr, beta1=beta1)
optimizer_G.update_parameters_name('optim_g.')
optimizer_D.update_parameters_name('optim_d.')

训练模型

训练分为两个主要部分：训练判别器和训练生成器。

训练判别器

训练判别器的目的是最大程度地提高判别图像真伪的概率。按照Goodfellow的方法，是希望通过提高其随机梯度来更新判别器，所以我们要最大化𝑙𝑜𝑔𝐷(𝑥)+𝑙𝑜𝑔(1−𝐷(𝐺(𝑧))logD(x)+log(1−D(G(z))的值。
训练生成器

如DCGAN论文所述，我们希望通过最小化𝑙𝑜𝑔(1−𝐷(𝐺(𝑧)))log(1−D(G(z)))来训练生成器，以产生更好的虚假图像。

在这两个部分中，分别获取训练过程中的损失，并在每个周期结束时进行统计，将fixed_noise批量推送到生成器中，以直观地跟踪G的训练进度。

下面实现模型训练正向逻辑：

def generator_forward(real_imgs, valid):
    # 将噪声采样为发生器的输入
    z = ops.standard_normal((real_imgs.shape[0], nz, 1, 1))

    # 生成一批图像
    gen_imgs = generator(z)

    # 损失衡量发生器绕过判别器的能力
    g_loss = adversarial_loss(discriminator(gen_imgs), valid)

    return g_loss, gen_imgs

def discriminator_forward(real_imgs, gen_imgs, valid, fake):
    # 衡量鉴别器从生成的样本中对真实样本进行分类的能力
    real_loss = adversarial_loss(discriminator(real_imgs), valid)
    fake_loss = adversarial_loss(discriminator(gen_imgs), fake)
    d_loss = (real_loss + fake_loss) / 2
    return d_loss

grad_generator_fn = ms.value_and_grad(generator_forward, None,
                                      optimizer_G.parameters,
                                      has_aux=True)
grad_discriminator_fn = ms.value_and_grad(discriminator_forward, None,
                                          optimizer_D.parameters)

@ms.jit
def train_step(imgs):
    valid = ops.ones((imgs.shape[0], 1), mindspore.float32)
    fake = ops.zeros((imgs.shape[0], 1), mindspore.float32)

    (g_loss, gen_imgs), g_grads = grad_generator_fn(imgs, valid)
    optimizer_G(g_grads)
    d_loss, d_grads = grad_discriminator_fn(imgs, gen_imgs, valid, fake)
    optimizer_D(d_grads)

    return g_loss, d_loss, gen_imgs

循环训练网络，每经过50次迭代，就收集生成器和判别器的损失，以便于后面绘制训练过程中损失函数的图像。

import mindspore

G_losses = []
D_losses = []
image_list = []

total = dataset.get_dataset_size()
for epoch in range(num_epochs):
    generator.set_train()
    discriminator.set_train()
    # 为每轮训练读入数据
    for i, (imgs, ) in enumerate(dataset.create_tuple_iterator()):
        g_loss, d_loss, gen_imgs = train_step(imgs)
        if i % 100 == 0 or i == total - 1:
            # 输出训练记录
            print('[%2d/%d][%3d/%d]   Loss_D:%7.4f  Loss_G:%7.4f' % (
                epoch + 1, num_epochs, i + 1, total, d_loss.asnumpy(), g_loss.asnumpy()))
        D_losses.append(d_loss.asnumpy())
        G_losses.append(g_loss.asnumpy())

    # 每个epoch结束后，使用生成器生成一组图片
    generator.set_train(False)
    fixed_noise = ops.standard_normal((batch_size, nz, 1, 1))
    img = generator(fixed_noise)
    image_list.append(img.transpose(0, 2, 3, 1).asnumpy())

    # 保存网络模型参数为ckpt文件
    mindspore.save_checkpoint(generator, "./generator.ckpt")
    mindspore.save_checkpoint(discriminator, "./discriminator.ckpt")

结果展示

运行下面代码，描绘D和G损失与训练迭代的关系图：

plt.figure(figsize=(10, 5))
plt.title("Generator and Discriminator Loss During Training")
plt.plot(G_losses, label="G", color='blue')
plt.plot(D_losses, label="D", color='orange')
plt.xlabel("iterations")
plt.ylabel("Loss")
plt.legend()
plt.show()

可视化训练过程中通过隐向量fixed_noise生成的图像。

import matplotlib.pyplot as plt
import matplotlib.animation as animation

def showGif(image_list):
    show_list = []
    fig = plt.figure(figsize=(8, 3), dpi=120)
    for epoch in range(len(image_list)):
        images = []
        for i in range(3):
            row = np.concatenate((image_list[epoch][i * 8:(i + 1) * 8]), axis=1)
            images.append(row)
        img = np.clip(np.concatenate((images[:]), axis=0), 0, 1)
        plt.axis("off")
        show_list.append([plt.imshow(img)])

    ani = animation.ArtistAnimation(fig, show_list, interval=1000, repeat_delay=1000, blit=True)
    ani.save('./dcgan.gif', writer='pillow', fps=1)

showGif(image_list)

从上面的图像可以看出，随着训练次数的增多，图像质量也越来越好。如果增大训练周期数，当num_epochs达到50以上时，生成的动漫头像图片与数据集中的较为相似，下面我们通过加载生成器网络模型参数文件来生成图像，代码如下：

# 从文件中获取模型参数并加载到网络中
mindspore.load_checkpoint("./generator.ckpt", generator)

fixed_noise = ops.standard_normal((batch_size, nz, 1, 1))
img64 = generator(fixed_noise).transpose(0, 2, 3, 1).asnumpy()

fig = plt.figure(figsize=(8, 3), dpi=120)
images = []
for i in range(3):
    images.append(np.concatenate((img64[i * 8:(i + 1) * 8]), axis=1))
img = np.clip(np.concatenate((images[:]), axis=0), 0, 1)
plt.axis("off")
plt.imshow(img)
plt.show()

最后打卡今天的学习时间

心得

我深入探索了DCGAN生成漫画头像的技术。DCGAN作为GAN的一种变体，通过巧妙地引入卷积和转置卷积层，极大地提升了图像生成的质量和效率。学习DCGAN原理，我了解到判别器和生成器的构建方式，以及它们如何通过对抗过程学习生成逼真的图像。特别是BatchNorm层和ReLU激活层的运用，为生成图像的多样性和稳定性提供了保障