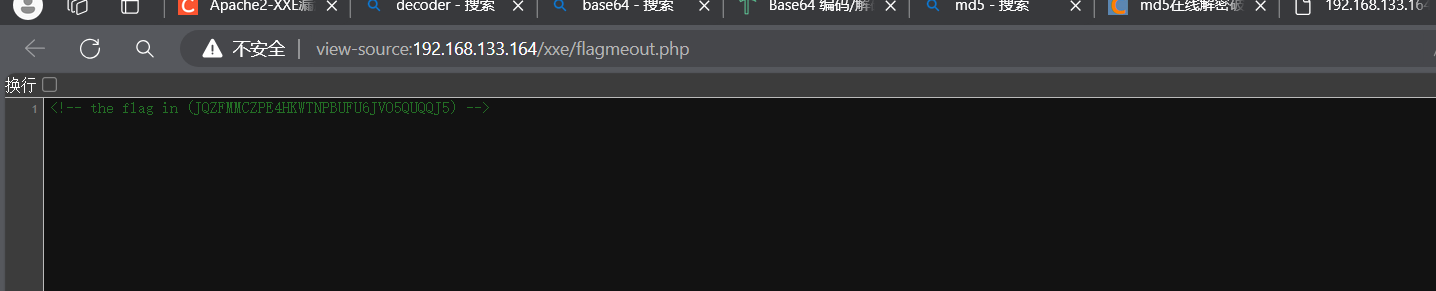
一些用来熟悉位操作符的应用
一、按位异或:^
异或运算:相同为0,相异为1
应用:在不引入临时变量(第三变量)的情况下,实现两个整数的交换。
关于两个整数交换,我们有一些方法,比如说,创建一个第三变量,就可以很轻易的实现两个整数的交换,如下代码:
#include <stdio.h>
int main()
{
int a = 10;
int b = 20;
printf("交换前:a=%d b=%d\n", a, b);
int c = a;
a = b;
b = c;
printf("交换后:a=%d b=%d\n", a, b);
return 0;
}但是,该程序引用了第三个变量,如果不引入第三个变量,我们又有什么办法来实现两个整数的交换呢?
这里我们就可以使用按位异或操作符^来达到想要的目的。
代码展示:
#include <stdio.h>
int main()
{
int a = 10;
int b = 20;
printf("交换前:a=%d b=%d\n", a, b);
a = a ^ b;
b = a ^ b;
a = a ^ b;
printf("交换后:a=%d b=%d\n", a, b);
return 0;
}相信你看到这个程序可能会有一点懵并充满疑惑,这是怎么实现的?
在解析这串代码之前,我们需要了解一些知识来为读懂代码做准备。
异或运算:相同为0,相异为1
int a =3;
int b = 5;
a的二进制表示:011
b的二进制表示:101
1. a^a = 0
a = 011
a = 011
a^a = 000
我们可以知道,整数和它自己本身异或得到的结果是0
2. a^0 = a
a = 011
0 = 000
a^0 = 011
我们可以得到,整数和0异或得到的结果是整数本身
当我们知道这些信息后,我们就可以解析这串代码了
a = a ^ b;
b = a ^ b;
a = a ^ b;开始时,将a ^ b的值赋给a,因此,b = a ^ b表达式中的a的值就变为a ^ b,通过异或运算,我们可以得到b=a,这时候,b的值就变为a了,但是a的值没有变化,还是 a ^ b,因此,在a = a ^ b表达式中, a ^ b中a的值还是a ^ b,b的值变为了a,通过异或运算,我们可以得到 a=b。
下面是图解:

图片或许表达的不是很清楚,如果有不明白的,可以私我,欢迎!
二、按位与:&
与运算:有0为0,全1为1
应用:求一个整数存储在内存中的二进制中1的个数
法一:通过判断整数的最后一位
int n = 15;
int count = 0;//二进制中1的个数将15与1进行 与运算 15&1
00000000000000000000000000001111 //15的二进制表示
00000000000000000000000000000001 // 1的二进制表示
00000000000000000000000000000001 //与运算结果
通过与运算结果是1,我们可以判断出15的最低位是1
因此,如果想得到n的二进制最低位,我们就可以给n按位与上一个1,通过判断结果是0还是1来确定n的二进制最低位是什么。
当我们得到最后一位后,如果结果是1的话,我们就count++,该最低位统计过后,我们需要统计倒数第二位,该怎么办呢?
我们可以通过右移操作符 >> 向右移动一位,这样就可以丢掉已经统计过的最低位,这样倒数第二位就来到了最低位,然后再按位与1,判断结果,如果结果是1,就count++,如果结果是0,则count的值不变,重复操作32次后,我们就可以判断完每一位是否为1,从而得到整数存储在内存中的二进制中1的个数。
for (int i = 0; i < 32; i++)//一个整型是4个字节,一个字节8个bit,这里的32就是32个bit位
{
if (((n >> i) & 1) == 1)
count++;
}这段代码使用一个循环来检查整数 n 的二进制表示中值为 1 的位的数量。 具体来说,循环从 0 迭代到 31 。对于每次迭代 i ,首先将 n 向右移动 i 位,然后与 1 进行按位与操作。如果结果为 1 ,说明 n 右移 i 位后的最低位是 1 ,此时就将计数器 count 的值增加 1 。当循环结束时,count 中存储的就是 n 的二进制表示中 1 的个数。
完整代码:
#include <stdio.h>
int main()
{
int n = 0;
scanf("%d",&n);
int count = 0;//二进制中1的个数
for (int i = 0; i < 32; i++)//一个整型是4个字节,一个字节8个bit,这里的32就是32个bit位
{
if (((n >> i) & 1) == 1)
count++;
}
printf("%d\n", count);
return 0;
}从上面代码,我们可以发现一些问题,就是不管所求数的二进制中有几个1,都需要循环32次
我们可以修改一下
法二:
int n = 13
表达式n = n & (n-1)
13的二进制序列:1101
n = n-1
第一组n和n-1
1101 --n
1100 --n-1
1100 --新的n
将新的n与原来相比,可以看到少了一个1,且是最后一位
第二组n和n-1
1100 --新的n
1011 --n-1
1000 --新的n
与第二个n相比,可以看到最右边的1又没了
第三组n和n-1
1000 --新的n
0111 --n-1
0000 --新的n
与上一个n对比,1又消去了。
从上面的例子,我们应该也能看出表达式n = n & (n-1)的作用:让n的二进制序列中最右边的1消失
n = n & (n-1)表达式每执行一次,就会去掉一个1,知道n中的1全部被去掉为止,因此,我们可以通过表达式进行的次数,来计算n二进制序列中有几个1
代码展示:
#include <stdio.h>
int main()
{
int n = 0;
scanf("%d",&n);
int count = 0;//二进制中1的个数
while(n){
n = n & (n-1);
count++;}
printf("%d\n", count);
return 0;
}该程序的好处是不会产生额外的循环,n的二进制序列中有几个1,就循环几次,没有就不循环。
三、按位或:| 按位取反:~
或运算:有1为1,全0为0
应用:将13的二进制序列的第5位修改位1,然后再改回0
13的二进制序列:00000000000000000000000000001101
将第5位置改为1:00000000000000000000000000011101
再将第5位改回0 :00000000000000000000000000001101
00000000000000000000000000001101
00000000000000000000000000010000
或结果:
00000000000000000000000000011101
那么00000000000000000000000000010000该怎么得到呢?
我们可以将1的二进制序列通过左移操作符向左移动4位 (1<<4)
这样就可以得到想要的结果了
代码展示:
#include <stdio.h>
int main()
{
int n = 13;
n |= (1 << (5-1));//将第5位0改为1
printf("%d\n", n);
return 0;
}那么我们该怎么改回去呢?
这里我们就要用到&和~了

因此,代码展示:
#include <stdio.h>
int main()
{
int n = 13;
n |= (1 << (5-1));//将第5位0改为1
printf("%d\n", n); //29
n &= (~(1 << (5 - 1)));//将第5位改回来
printf("%d\n", n);//13
return 0;
}
本篇文章到这里就结束了,期待你们的下次到来!!!