供应链|OR论文解读：具有内生随机交货期的双源库存最优策略

编者按

本次解读的文章发表于 Operations Research，原文信息：Song, J. S., Xiao, L., Zhang, H., & Zipkin, P. (2017). Optimal policies for a dual-sourcing inventory problem with endogenous stochastic lead times. Operations Research, 65(2), 379-395.
关键词：双源；动态规划；库存策略；最优控制；随机提前期；串联队列

问题背景

从第二次工业革命开始，近代工业生产逐渐标准化实现规模效应大幅降低生产成本，轮船、火车等交通工具的也因为动力技术的提升、集装箱标准化让超大规模、远距离运输成为可能。此外，不同国家之间的工业发展程度的差异，也导致了特定产品在发展中国家和发达国家中的制造成本的价差。交通方式的改变和价差的存在，为全球化贸易创造了条件。随着1947年关税与贸易总协定的生效，近代全球化贸易体系逐渐形成，制造商可以搜寻其他国家的原材料供应商，其采购策略也逐渐发生变化。

20世纪诸多实证研究表明，众多企业已经采用双源采购（dual sourcing）的方法，来对冲单一供应商其生产或运输过程中断或长时间延误的风险，以提高企业制造过程的敏捷性，应对可能的市场需求波动的情况。同时，双源采购也可以通过采购拍卖和竞争性招标的方式，帮助企业消除采购过程中的信息不对称、从而降低采购成本。

双源采购（Dual Sourcing）：这种策略指的是企业从两个不同的供应商采购同一种物料或产品。这种做法的目的是为了降低供应风险，提高供应链的灵活性和稳定性。如果一个供应商出现问题，另一个供应商可以提供支持，确保供应的连续性。

多源采购（Multiple Sourcing）：这种策略指的是企业从两个以上（即多个）不同的供应商采购同一种物料或产品。相比双重采购，多源采购进一步分散了供应风险，因为依赖于更多的供应商，即使有一个或多个供应商出现问题，其他供应商也能提供支持。

双源采购涉及到对供应商地理位置、货物运输方式的选择。一般认为，从海外供应商采购（global sourcing）的采购成本低于当地采购（domestic sourcing），但当地采购可以提供更短的交货期（lead time），即采购方从开始下单订购到供应商完成生产准备交货中间所间隔的时间更短。类似地，海陆运输（shipping）的成本就比航空运输（air transportation）要低，时间更长。此外还有其他因素也可能影响采购者对供应商的选择，如产品质量、供应商生产能力、供应商履约率等，因此多源采购往往可以抽象为一个权衡采购成本和供应商服务质量的决策（过程）。

而在诸多关于多源采购的文献中，产品采购一般都按照订单交货期长短分为紧急补货（emergency replenishment）和常规补货（regular replenishment）两种方式。管理者在制定补货订单时需要决定如何准确地部署这两个源，即在什么时间向不同的两个供应商订货、以及订多少货。

关于双源采购最优策略的研究现在有两条主流：其一是在交货期确定（deterministic lead time）假设下的周期性检查策略（period-review），但截止原文章发表，研究发现，仅当两种补货方式的交货期相差不超过一个时期时最优政策的清晰结构。其二则是在交货期随机（stochastic lead time）假设下，使用系统参数来刻画最优策略，而如何准确的定义交货期时间的分布，则是该方向的主要挑战。

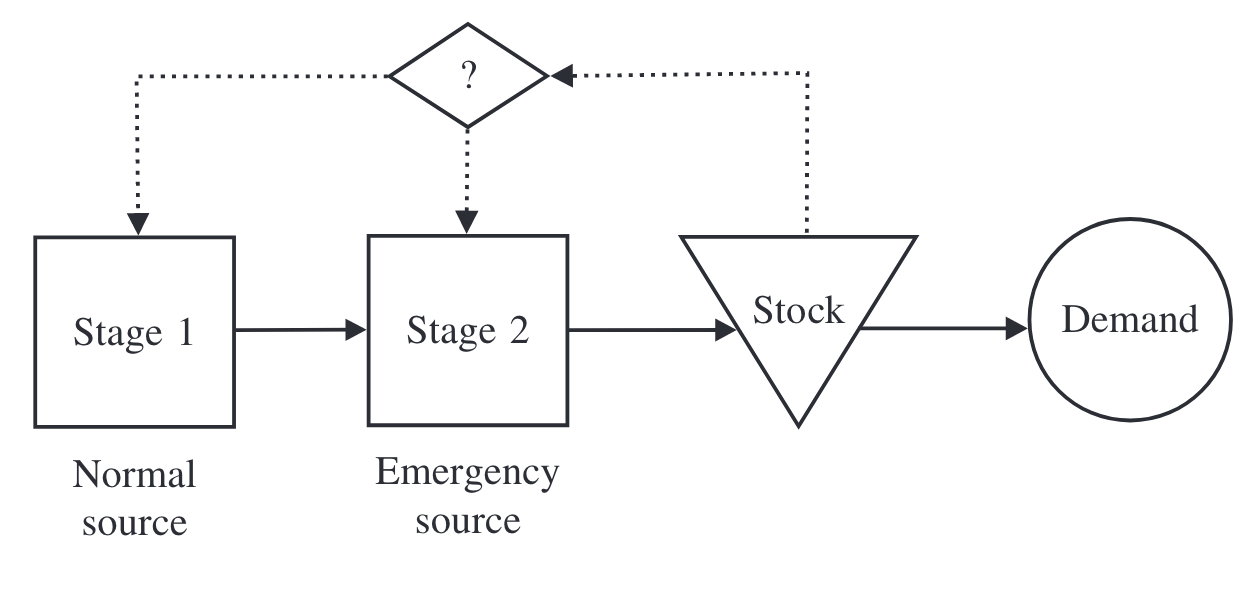
文章中的模型采用了两个服务器的串联系统（tandem queue system）来描述常规供应和紧急供应的交货期差异：

两个服务器的服务时间各自独立且服从不同的分布；常规订单会经过两个服务器，紧急订单则跳过第一个服务器、直接进入第二个服务器，所有订单在第二服务器处理后进入库存用于满足市场需求，因此常规订单的交货期是两个服务器时间之和。

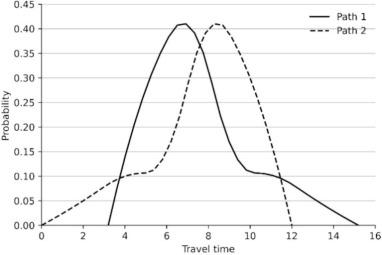
文章的模型模拟了产品从运输到生产整个流程，第一服务器可以视为下订单后货物的运输过程，第二服务器可以视为货物到达后的加工流程，跳过第一阶段则代表紧急订单运输所需时间为 0. 因此，常规订单和紧急订单可以分别理解为海外采购和本地采购。类似地，该模型也可以模拟货物运输方式的选择，常规订单往往采用成本较低的多种运输方式联合转运（如远洋货运配合目的地的卡车转运），紧急订单则用单一运输方式直接运输到采购方。交通相关实证研究表明，由于拥堵、更换运输工具等原因，某些货物的（常规）运输的总时间确实符合多峰分布(multimodal distrubtion). 虽然用一个串联系统来模拟整个生产和运输过程只是一个粗略的近似，但文章提供了可以处理的、并有定性分析结论合理的起点。

模型构建

承接上文，文章的模型巧妙地模拟了两种采购方式交货期之间的关联，同时本文采取了新颖的方法分析模型结构、得出的最优策略也解释了对管道库存（pipeline inventory）以及对应的成本在采购决策中的重要性。

管道库存 (pipeline inventory),亦为“在途库存”或“运输库存”，指正在运输途中的库存，即从供应商发货后到达目的地之前的货物。

用 O 表示原系统，构造如下图。其中，当时间为 $t$ , $N_1(t)$ 和 $N_2(t)$ 表示服务器1和服务器2正在处理或者等待处理的任务数量， $I N (t)$ 则表示净库存数量（即在手库存减去未满足库存 on-hand inventory - backorders），系统状态由 $IN(t),N_2(t), N_1(t))$ 表示。同时假设 $f (x, y, z)$ 为系统起始状态为 $(x, y, z)$ 时的最优成本，其中 $N_2(t),N_1(t))=(x,y,z)\in\mathbb{Z}\times\mathbb{Z}^2_{+}$ . 原文分析的基本思想是，将原三维系统简化为一个等价的、易于处理的二维系统。

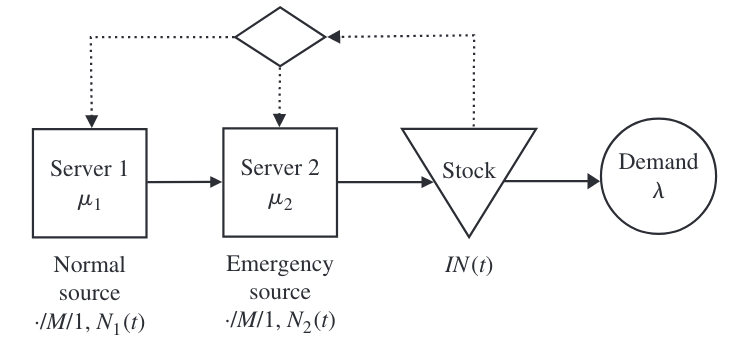
首先，文章的系统由以下几组参数刻画：

$c_i$ : 系统 M 中，当 $i = 1, 2$ 时，分别表示普通订货、紧急订货的单位采购成本。

$h_i$ : 系统 M 中，当 $i = 1, 2$ 时，分别表示单位时间内普通订货、紧急订货服务器中，等待或正在处理的订单持有成本。

$\mu_i$ : 当 $i = 1, 2$ 时，分别表示普通订货、紧急订货服务器的处理时间指数分布的速率。

$\alpha$ : 成本折旧率。

$h$ : 单位时间单位成品作为库存 (stock) 的持有成本。

$b$ : 单位时间单位成品的缺货成本。

文章改变第一个服务器对订货成本的收费方式，是生成一个新系统，称为系统 M. 在原系统 O 中，服务器1（即常规采购）的订货成本是下订单时产生的，而系统M常规采购的订货成本在订单完成时产生。令 $\tilde{c_1}$ 表示系统O中，普通订货的单位采购成本。动态规划的方法可以证明，当两个系统的最优成本满足 $\tilde{c}_1 = \frac{\mu_1 + \alpha}{\mu_1}c_1$ ，系统 M 的最优策略与系统 O 相同，即当服务器 1 不为空 ( $z > 0$ ) 时，不下普通订单，服务器2不为空时 ( $y > 0$ ), 不下紧急订单（详见原文引理2）。
其次，作者将三维系统 M 简化为二维系统，称为系统 A（见下图）。为了构造系统A，作者改变了系统M中在服务器1下订单的动作，并且在服务器1处没有队列。系统制服务器1的服务速率， $\mu_1$ 表示最大服务率。由此，系统A的状态由 $IN(t),N_2(t))$ 表示

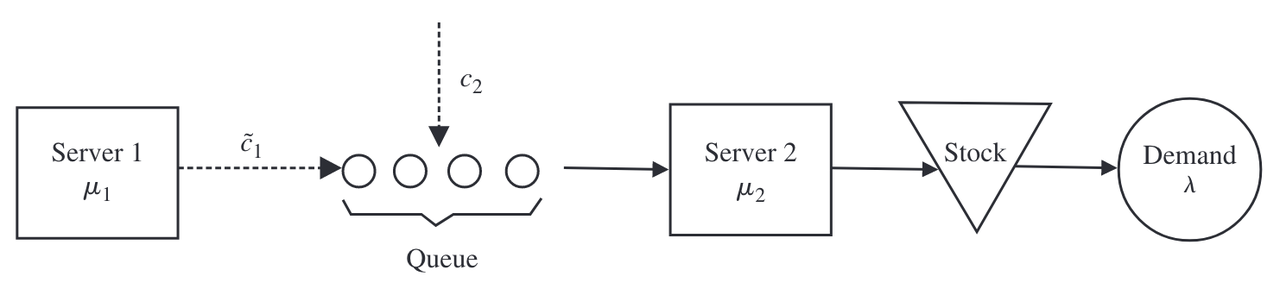
对于系统A，文章通过两步分析，刻画了其最优策略。

对于系统A，起始状态 $(x, y)$ 对应的最优成本 $\tilde{f}(x,y)$ 应当满足以下贝尔曼方程：

其中最后一项 $\tilde{\mathscr{T}}\tilde{f}(x,y)$ 可以进一步展开，并且发现仅根据 $\nabla_y \tilde{f}(x,y)+\tilde{c_1}$ 即可确定最优政策。因此，作者进一步定义： $\min\{x:\nabla_y \tilde{f}(x,y)+\tilde{c_1}\geq 0\}$ .

当系统状态为 $(x, 0)$ 时，可以计算得出$ S(1)<S(0) $, 最优策略有以下：

当$ x<S(1)$时，最优策略为打开服务器1，服务器2是否向库存供应皆可。
当$ S(1) \leq x < S(0)$时，最优策略为打开服务器1，服务器2不供应，或者关闭服务器1，服务器2供应。
当$ x \geq S(0) $时，最优策略为关闭服务器1，服务器2是否向库存供应皆可。
为了确定每个区间中的最优策略，作者进一步给出阈值 $R$ 的表达式，并得到以下三种情况及其最优策略。

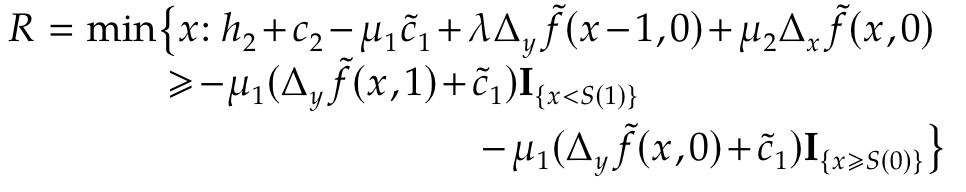
最后，作者提出并证明，当系统参数满足 $h_2 + c_2(1 -\lambda) - \mu_1 \tilde{c_1} \geq \mu_2 b / \alpha$ 时，系统 A 的最优策略也是系统 O 的最优策略（详见原文命题1、命题2）。

策略解读

本文模型的最优策略可以用固定阈值来刻画：向服务器2发送订单的固定阈值 $R$ 和向服务器1发送订单的阈值（由服务器2 (记 $S(\cdot)$ 处的状态函数给出）来刻画。当参数满足 $R\geq S(1)$ 时，使用由串联队列的策略构造出的启发式策略。

三个系统的最优策略都符合直觉：无论是常规采购还是紧急采购，只要管道库存不为0，都不应该下单补货，而应该等待在运输途中的货物运到；因为下单越晚的货物越晚到的概率更大（比前一单货物提前到的概率非常小）。

数值实验及比较

文章的第6章基于前文提出的等价系统以及前提条件，进行了两大类比较。对于不满足等价条件、且 $h_2 \geq h$ 的系统，作者提出了启发式算法，并将结果和两个现有策略（Dual Index P）进行比较。对于 $h_2 < h$ 的系统，文章也提出了启发式算法并进行了数值试验。

阈值曲线策略（Threshold Curve Policy, TC Policy）

首先，对 $h_2 \geq h$ 的原系统O，最优策略取决于净库存 $I N$ 和阈值 $R$ 等参数（详见原文第5章第2节定理3）。
鉴于这种观察，假设修改系统A的这一部分策略，以获得系统 O 的可行策略。当 $I N < S (1)$ 且 $N_2 =0$ 时，从服务器2订购，如果服务器1处于空闲状态，也在服务器1处订购；当 $I N$ 从小于接近 $S (1)$ 且 $N_2 =0$ 时，在服务器2下单，在服务器1不做任何操作。(实际在这种情况下，服务器1已经在处理一个订单。) 当 $S (1) < I N < R$ 且 $N_2 =0$ 时，在服务器2下单，在服务器1不做任何操作。我们称这种策略为阈值曲线 (TC) 策略。
下表的实验结果表明TC策略的最优性差距（optimality gap）在多种情况下都非常小。

双指标策略（Dual Index Policy, DI Policy）

策略中的双指标表示两种库存水平（inventory positions）
$IP_1(t) = IN(t)+ N_2(t)+ N_1(t),$
$IP_2(t) = IN(t)+ N_2(t).$
本文在双策略指标的基础上，将其转换为串联系统，并且求出该系统中两个服务器中订单个数之和（ $N_1 + N_2$ ）的概率分布。基于以上推导，作者提出了改进版的双指标策略（Smart Dual Index Policy, SDI Policy）:
当 $IP_2(t) < s_2$ ，服务器2（紧急供应）空闲时，使用向紧急供应下单。
当 $IP_1(t) < s_1$ ，服务器2（常规供应）空闲时，使用向常规供应下单。

参数满足条件 $s_1 \geq s_2$ .

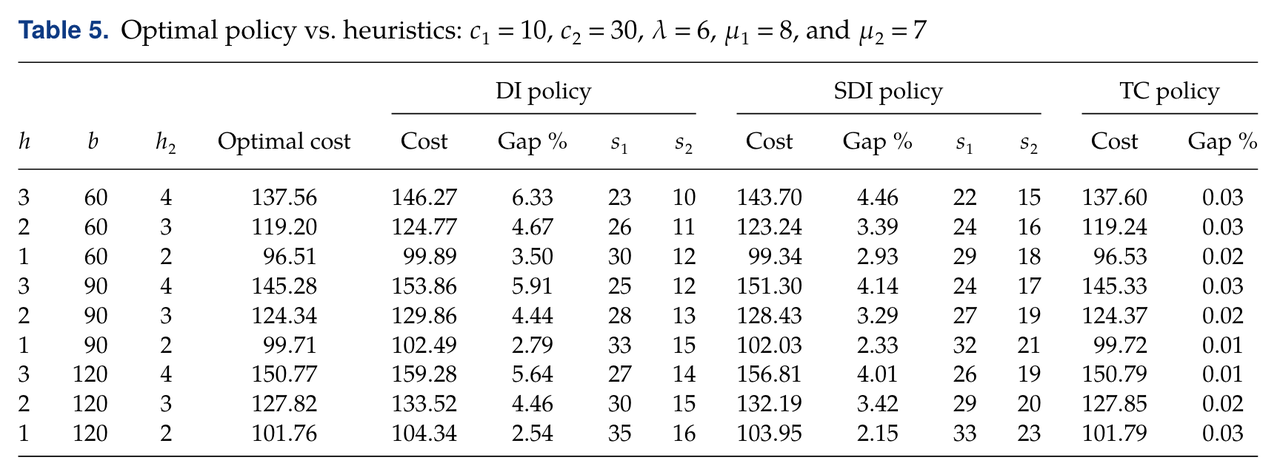
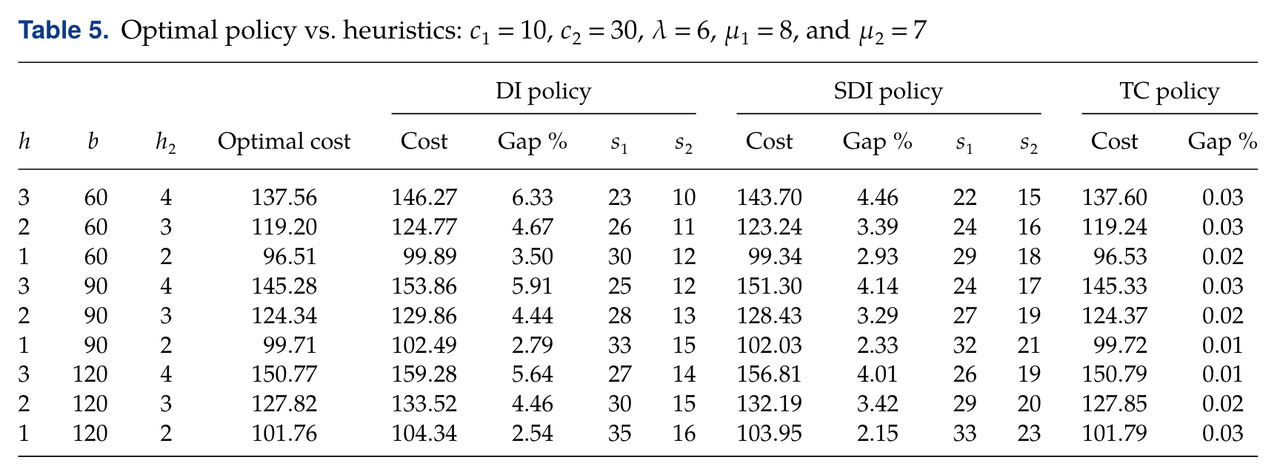
下表展示了数值试验结果。原文中展示了多种系统设定，结构都表明三种策略中：TC 策略远优于两种双指标策略，同时SDI策略略优于DI Policy。从直觉上理解，阈值曲线策略可以动态地调整触发紧急订单的阈值 $S(N_2)$ ，但是两种双指标策略的阈值都是固定的参数 $s_1$ ，由根据系统设定计算得出。

定制基数-激增策略（Tailored Base-Surge Policy, TBS Policy）

TBS策略由两部分操作构成，其一是通过常规采购周期性的预定固定数量的订单，其二是当系统中的库存数量低于阈值基本库存水平的（base-stock level，用 $s$ 表示）时，预定紧急订单将库存水平补充到基本库存水平。因此，该策略的关键在于确定两个参数：周期性的常规订货的数量、触发紧急订货的 $s$ 。
在文章的串联系统中，基本库存水平 $s$ 本质上可以理解为服务器1的固定速率 $\mu_1$ , 因此假设给定范围 $[0,\mu_1]$ ，可以通过马科夫链的分布得到 $\mu_1^\prime \in [0,\mu_1]$ 系统平均成本，由此确定最优速率 $\mu_1^*$ .
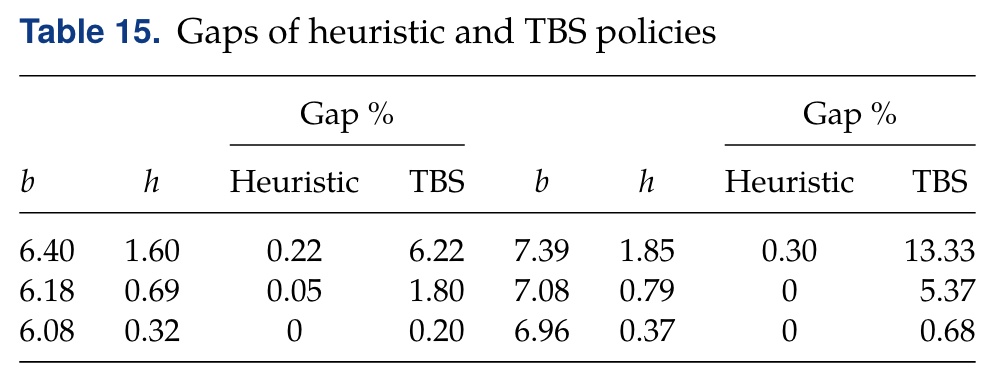
数值实验结果表明，当需求的到达速率增加时，TBS策略的表现逐渐提升，其原因在于需求低时，TBS策略中的服务器1（常规订货渠道）并未被完全使用，而TC策略则可以动态调整阈值，使得系统可以更充分的利用常规订货渠道（详见原文表格8如下）。

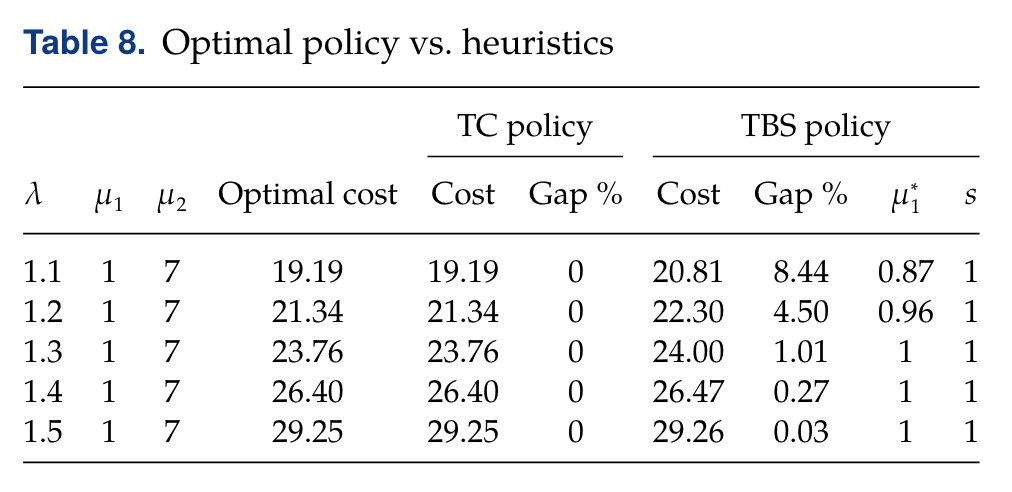
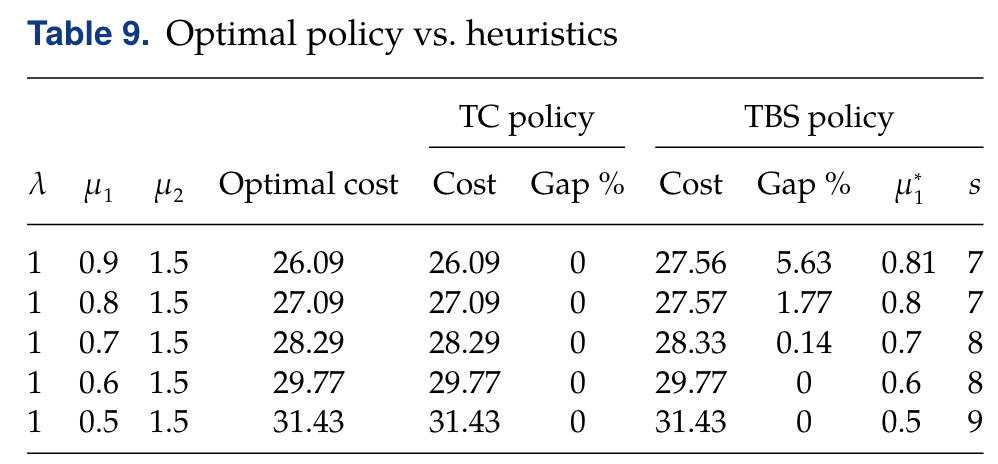
此外，TBS策略的最优性差距也随着常规采购和紧急采购前置时间的差值增大而减小。

策略中的双指标表示两种库存水平（inventory positions）
$IP_1(t) = IN(t)+ N_2(t)+ N_1(t),$
$IP_2(t) = IN(t)+ N_2(t).$
本文在双策略指标的基础上，将其转换为串联系统，并且求出该系统中两个服务器中订单个数之和（ $N_1 + N_2$ ）的概率分布。基于以上推导，作者提出了改进版的双指标策略（Smart Dual Index Policy, SDI Policy）:
当 $IP_2(t) < s_2$ ，服务器2（紧急供应）空闲时，使用向紧急供应下单。
当 $IP_1(t) < s_1$ ，服务器2（常规供应）空闲时，使用向常规供应下单。

参数满足条件 $s_1 \geq s_2$ .

下表展示了数值试验结果。原文中展示了多种系统设定，结构都表明三种策略中：TC 策略远优于两种双指标策略，同时SDI策略略优于DI Policy。从直觉上理解，阈值曲线策略可以动态地调整触发紧急订单的阈值 $S(N_2)$ ，但是两种双指标策略的阈值都是固定的参数 $s_1$ ，由根据系统设定计算得出。

TC策略的鲁棒性：当服务器的处理时间为确定值时，TC策略仍然有很好的表现。

TC策略整体优于TBS策略，但当 $\lambda$ 值较大或两个服务器前置时间差值较大时，两种策略的表现趋同（和处理时间指数分布的情况观察到的趋势一致）。详情见原文表格10、11。
类似的，实验结果表明TC策略整体优于DI。当 $\lambda$ 值较小时，TC策略和DI策略的最优性差距比较接近。SDI策略则和TC策略的表现几乎一致。其原因在于，当 $\lambda$ 值较小时，三种策略出发紧急订单的概率都比较小，因此采取的行动（action）都比较接近。详情见原文表格12、13。

$h_2 < h$ 条件下的启发式策略

该策略首先构造出与原系统等价、 $h_2 = h$ 的新系统，并找新系统的最优策略，再由此推断出原系统的策略。
和双指标策略相比，该启发式策略的表现优于DI策略，逊于SDI策略，且随着服务器的服务水平的提升，该启发式策略的表现也逐渐提升。作者分析，由于服务水平提升，系统库存的成品数量升高、策略会更少地使用紧急订货，从而减小最优性差距。

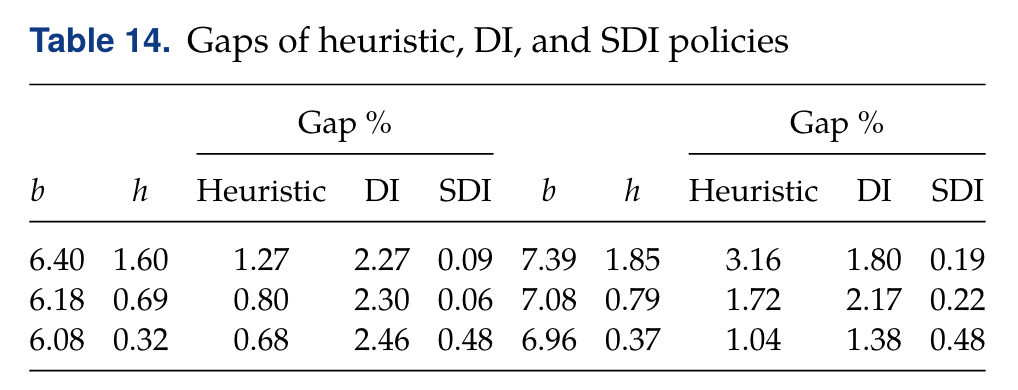
和TC策略类似，启发式策略比TBS策略表现更好，二者的最优性差距也都随服务水平提升而减小。

结论

文章将多源采购问题转化为两个串联单服务器排队模型，进一步将其简化，并通过简化系统的最优策略来表示出采购最优策略，从而可以精确地量化各种启发式算法的性能。

文章巧妙地证明了多源采购，在具有内生随机的前置时间的情况下，具有可以采用参数表示的阈值、并根据阈值分段的最优策略。
文章的分析基于指数加工时间（processing time），通过扩展动态规划的状态空间，类似的最优策略可以推广到服从Erlang分布的加工时间模型或其他马尔可夫供应网络。
文章所提出的阈值曲线策略策略和启发式策略都使用了供应系统的实时信息，包括给定时间时，哪些服务器是繁忙的、系统的净库存水平等，从而实现了对于触发紧急订货的阈值的动态调整。因此，文章提出的策略可以更有效地在实际中降低系统的采购成本。从实际的商业采购角度看，TC策略也证明了管道库存在多源采购的决策中的关键作用，启示企业在管理和采购决策时可以考虑更多的信息。