摘要

现实世界中的交通网络通常具有随机特性，旅行时间可靠性自然成为影响旅行者路线选择的关键因素。在这种情况下，仅凭平均路径旅行时间可能无法充分代表路径对旅行者的吸引力，本研究引入了 $k$ 阶均值偏差模型，用于优化大型、随机和时变网络中的路线选择

关键词： 交通网络随机性、旅行时间可靠性、均值偏差模型

1.引言

现实世界中的交通网络通常具有随机特性，旅行时间可靠性自然成为影响旅行者路线选择的关键因素。在这种情况下，仅凭平均路径旅行时间可能无法充分代表路径对旅行者的吸引力，因为它可能会导致冒险的选择。因此，考虑可靠性的路线选择模型的制定和求解成为关键的研究课题。

本研究引入了 $k$ 阶均值偏差模型，用于优化大型、随机和时变网络中的路线选择。该模型通过更好地处理旅行时间的极端结果来解决传统平均标准偏差方法的局限性。它具有一个名为“旅行时间预算（travel time budget）”的目标函数，它将平均路径旅行时间与安全边界(average path travel time with a safety margin)相结合。该边界由权衡系数和旅行时间的选定偏差度量总偏差或半偏差total or semi）定义。该模型分为三个变体：

1）用于对称旅行时间分布的平均总偏差 (mean-total deviation, MTD) 模型

2）用于非对称分布的平均上半偏差 (mean-upper-semi-deviation, MUSD) 模型，考虑上半偏差，适合规避风险的旅行者

3）用于非对称分布的平均下半偏差 (mean-lower-semi-deviatio, MLSD) 模型，考虑下半偏差，适合风险倾向的旅行者

均值风险模型

模型分析

均值风险模型是表达路径可靠性的经典模型。在均值风险分析框架中，出行者在选择最优路径时，既考虑出行时间的均值，也考虑出行时间的风险（即变化）。因此，路径的成本由两个部分组成：平均出行时间和相关风险。该框架的一个显著优势是它能够直接从实际数据中得出所需的数据，从而无需找到合适的分布或对随机出行时间做出假设。

均值风险分析框架的核心问题是如何衡量风险。通过路径行程时间的标准差（或方差）来量化风险通常被认为是最普遍和行为最直观的方法。这类以标准差（或方差）作为风险项的模型，通常称为均值-标准差（或均值-方差）模型。其目标是最小化平均路径行程时间与安全边界的总和，其中安全边界定义为权衡系数乘以路径行程时间的标准差（或方差）。权衡系数体现了出行者的风险偏好：风险规避程度越高，权衡系数也就越大。

虽然用标准差或方差来表示风险是很自然的，但它仍然存在一些缺点。方差本质上是随机变量与其均值的偏差平方的加权和，其中权重是概率密度。因此，它揭示的有关低概率密度的尾部分位数（即极值）偏差的信息较少。标准差是方差的平方根，它继承了这个缺陷。如果所考虑的概率分布具有长尾，那么规避风险的决策者可能会高度关注极值。在这种情况下，标准差和方差不足以表征风险，因此均值-标准差模型和均值-方差模型都不能很好地捕捉决策者的选择行为。

为了说明这一点，让我们看一个两条路线的例子。

一个小例子

例子：对于两条给定的路线，其行驶时间的分布律如下表所示。两条路线的均值、标准差和方差完全相等，分别为18，3.156，9.96。

旅行时间	路线 1	路线 2
10	0.02	0.025
12	0.03	0.045
14	0.11375	0.08
16	0.2	0.12
18	0.2725	0.46
20	0.2	0.12
22	0.11375	0.08
24	0.03	0.045
26	0.02	0.025

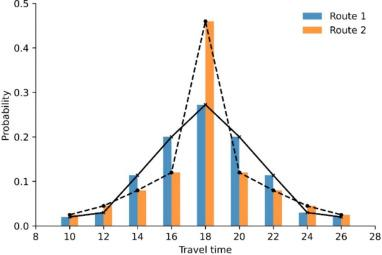
因此，在均值-标准差或均值-方差决策模型中，旅行者对两条路径没有偏好，权衡系数将失灵。但是分析分布的右尾时，发现一个明显规避风险的个体，比如一个需要至少 95% 的准时到达概率的旅行者，可能会倾向于路线 1。这种偏好归因于路线 1 的旅行时间超过 22 个单位的概率只有 5%，而路线 2 的概率为 7%。同样，一个极度倾向于冒险的旅行者可能会因为类似的考虑而选择路线 2，因为路线 2 的旅行时间分布具有更明显的尾部。

综合均值偏差建模框架

概述

考虑$k$阶总偏差，开发平均总偏差模型，以更准确地表示大型随机交通网络中旅行者的风险相关路线选择行为。$k$描述了旅行者对极端事件的态度，阶数越大，模型将更好地表现极值偏差平均值的能力。经典的均值标准差模型属于$k=2$的特例。

此外，为了揭示概率分布的偏斜性，从而更好地捕捉旅行者的路线选择行为，$k$阶总偏差可以分为$k$阶上偏差和$k$阶下偏差。由此得到两个派生模型：the mean-upper-semi-deviation (MUSD) 模型和 the mean-lower-semi-deviation (MLSD) 模型。这两个派生模型与MTD模型一起统称为新的综合均值偏差框架。

对称行程时间分布的平均偏差模型

总风险的定义

在均值风险分析领域，人们认为旅行者的目标是尽量缩短平均旅行时间，同时降低相关风险。因此，模型表明，在选择最佳路线时，旅行者会寻求最小化目标函数，该函数由${\mu }_X+\lambda {\delta }_X$。其中${\mu }_X$表示X的均值，${\delta }_X$表示X的安全边界，$\lambda$表示权衡系数。需要注意的是，在实际情况下，𝑋总是非负的，这使得$X\in [0,+\infty )$。${\delta }_X$通常用标准差来表示。但是，我们定义了更一般的形式：

$${\delta }_X^{(k)}=[E(|X-{\mu }_X){|}^k{]}^{1/k}=({\int }_0^{+\infty }(X-{\mu }_X{)}^{k}d{F}_X(x){)}^{1/k}$$
当$k=1$时，得到的一阶总偏差：
$${\delta }_X^{(1)}=({\int }_0^{+\infty }|X-{\mu }_X{|}^{k}d{F}_X(x))$$
当$k=2$时，得到的二阶总偏差：
$${\delta }_X^{(2)}=[E(|X-{\mu }_X){|}^2{]}^{1/2}=({\int }_0^{+\infty }(X-{\mu }_X{)}^{2}d{F}_X(x){)}^{1/2}$$
我们有上半偏差$\overline{{\delta }_X^{(k)}}$和下半偏差$\underline{{\delta }_X^{(k)}}$：
$$\begin{gathered} \underline{{\delta }_X^{(k)}}=({\int }_0^{\mu }(X-{\mu }_X{)}^{k}d{F}_X(x){)}^{1/k} \\ \overline{{\delta }_X^{(k)}}=({\int }_{\mu }^{\infty }(X-{\mu }_X{)}^{k}d{F}_X(x){)}^{1/k} \end{gathered}$$
考虑积分的可加性，进一步有：
$$\begin{gathered} (\underline{{\delta }_X^{(k)}}{)}^k=({\int }_0^{\mu }(X-{\mu }_X{)}^{k}d{F}_X(x){)}^{1/k} \\ (\overline{{\delta }_X^{(k)}}{)}^k=({\int }_{\mu }^{\infty }(X-{\mu }_X{)}^{k}d{F}_X(x){)}^{1/k} \\ ({\delta }_X^k{)}^k=(\overline{{\delta }_X^{(k)}}{)}^k+(\underline{{\delta }_X^{(k)}}{)}^k \end{gathered}$$

均值总风险模型

考虑$k$阶总偏差时，均值风险模型将转化为均值总风险模型。对应的目标函数的公式表述为：
$$mi{n}_p:{\mu }_p+\lambda {\delta }_p^{(k)}$$
这里的$p$表示任意OD对儿之间的路径，$\lambda ,k$表示模型参数，${\mu }_p,{\delta }_p^{(k)}$分别表示均值和$k$阶总偏差。

例子的进一步解释

回到刚开始的小例子，两条路线的标准差相等，为 3.156。一阶总偏差为：路线 1 为 2.39，路线 2 为 2.06，表示旅行时间与各自均值的平均绝对偏差。三阶总偏差为：路线 1 为 3.713，路线 2 为 3.853。虽然标准差无法辨别路线 1 和 2 之间的差异（因为它们的均值和方差相同），但一阶和三阶总差可以有效捕捉其旅行时间分布尾部行为的差异。

使用一阶总偏差来评估与旅行时间变化相关的风险意味着人们更倾向于选择路线 2，而不是路线 1。这种情况适用于风险规避程度相对较低的旅行者，例如只需要 65% 或更高准时到达概率的旅行者，对应路线1的时间要求为18个单位，路线2的时间要求为20个单位。如果旅行者追求95%的准时偏好，则三阶偏差正好契合了这种选择。

造成这种差异的主要原因在于一阶偏差、标准偏差和三阶偏差对极值的反映不同。虽然这三个指标都可以用来表示随机变量与其平均值的平均偏差，但它们对极值的描述存在明显差异。在一阶偏差的情况下，极值的影响相对有限，而标准偏差和三阶偏差都赋予极值的权重更大。随着偏差阶数的增加，极值的反映变得更加充分。这些指标共同描述了旅行者对同一随机旅行时间波动的不同风险感知水平。因此，为了准确捕捉旅行者的路线选择行为，在量化风险时，仔细选择偏差阶数是关键，因此需要将偏差阶数作为参数纳入路线选择模型。

$\lambda ,k$表示模型参数，前者表示每单位风险的成本（以时间来衡量），后者揭示了旅行者对极值的态度。

• $\lambda$ 为正表示出行时间预算大于$\mu$，$\lambda$ 为负表示出行时间预算小于$\mu$，因此，$\lambda$ 可以作为衡量旅行者冒险倾向程度的指标，也可以用来模拟旅行对旅行者的重要性。
• 参数$k$揭示了旅行者对极端价值的态度，$k$越大表示旅行者更关注极端值。

因此，$\lambda$ 为正且固定时，一个更大的$k$意味着通常会预留更多的时间预算，并变得更加规避风险。

如果旅行者分配的行驶时间由$\mu +\lambda {\delta }^{(k)}$决定，夹着行驶时间服从正态分布，则有：
$$P(X\le \mu +\lambda {\delta }^{(k)})=P(\frac{X-\mu }{\delta }\le \lambda \frac{{\delta }^{(k)}}{\delta })=\Phi (\lambda \frac{{\delta }^{(k)}}{\delta })$$

非对称行驶时间分布的均值半偏差模型

之前的讨论中，我们都假设X的分布是对称的，但是对于不对称的分布，${\delta }^{(k)}$不能代表偏斜(skewness)，这是旅行者在评估不同路径的旅行时间预算时通常关心的一个关键因素。可以提供以下说明性示例来演示这一概念。

一个反例

假设路径1和2是随机网络中从起点到终点的两条路径。它们各自的行程时间分布、平均行程时间、标准差以及下限和上限半标准差报告如下：

路线	行驶时间	概率	均值	标准差	下半偏差	上半偏差
路线1	5.2	0.3	7.60	2.24	1.34	1.80
	7.2	0.4
	9.2	0.15
	11.2	0.1
	13.2	0.05
	0.2	0.12
路径2	2	0.05	7.60	2.24	1.80	1.34
	4	0.1
	6	0.15
	8	0.4
	10	0.3

两条路径具有相同的均值、标准差、下半偏差和上半偏差都相同，而且对于任意$k$，他们的${\delta }^{(k)}$也相等。因此，均值标准偏差模型将无法区别两条路径的差异，但是实际上，这两条路径并不相同。结果发现路径1具有正偏的旅行时间分布，而路径2具有负偏的旅行时间分布。这种差异对旅行者的路径选择有重要影响。

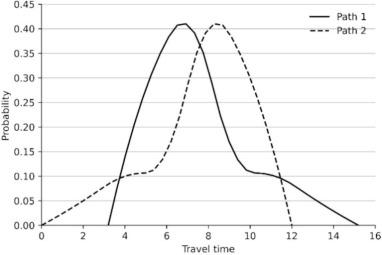
路径1的旅行时间可能延长至13.2 个单位，而路径2的旅行时间保证不超过10 个单位。因此，为了避免迟到，风险规避型旅行者倾向于为路径1预留更多时间。相反，由于路径 2 的负偏性𝑋，一个倾向于冒险的旅行者可能愿意冒险并为路径2分配较少的时间预算。毕竟，路径2的旅行时间短至2 个单位的可能性为5%。

均值上半偏差 (MUSD) 模型

上述例子表明，规避风险的旅行者往往会更多地考虑𝑋位于均值右侧的部分，而风险偏好型旅行者更关心左侧部分。这些正是上半离差和下半离差分别关注的部分。因此，衍生出两个均值半离差模型：均值上半离差 (MUSD) 模型和均值下半偏差 (MLSD) 模型：
$$\begin{gathered} MUSDmi{n}_p:{\mu }_p+\lambda \overline{{\delta }_p^{(k)}} \\ MLSDmi{n}_p:{\mu }_p+\lambda \underline{{\delta }_p^{(k)}} \end{gathered}$$
均值上半离差 (MUSD) 模型专为规避风险的旅行者设计；均值下半偏差 (MLSD) 模型为风险倾向型旅行者量身定制。

进一步，令$\lambda >0$，与 MTD 模型相比，MUSD 模型$mi{n}_p:{\mu }_p+\lambda {\delta }_p^{(k)}$更适合模拟规避风险的旅行者的路线选择；对于风险倾向高的旅行者，MLSD 模型$mi{n}_p:{\mu }_p-\lambda {\delta }_p^{(k)}$优于MTD。

参考文献：

Liu, Y., Xiao, F., Shen, M., Zhao, L., & Li, L. (2024). The k-th order mean-deviation model for route choice under uncertainty. Transportation Research Part E: Logistics and Transportation Review, 189, 103646.