背景

在移动数字广告营销的整个链路中，主要有三个主体，分别是媒体、adx和dsp.对于一个adx系统，主要有两个功能，分别是：

1. 向下对接媒体：汇聚下游的媒体广告流量

2. 向上对接dsp(广告主)：将媒体流量卖给上游dsp(或广告主)，获取收入。

adx作为一个流量汇聚平台，一方面从广告主那里获取广告投放收入，一方面使用媒体侧的广告位流量，需要支付费用给媒体。这一收入、一支出是adx营收的主要方式，并以此获取利润。

而智能出价系统主要解决的问题就是：如何在收入和支出之间，保证毛利额最大化的问题？在这个问题中，一般来说，收入侧就是通过rta(实时竞价系统)以一价或二价方式和dsp进行成交的价格，但今天所研究的问题是平台成交价已知(或确定)的情况；那就引出另外一个问题，就是在收入确认的情况下，如何规划支出，才能保证毛利额的最大化，因为：

毛利额= 平台成交价 - 媒体成交价

但是在实际的业务场景中，毛利额并不是这么简单的减法问题，因为这里面还涉及到曝光率的问题，具体来说涉及两个问题：

3. 给媒体出低价：毛利额高，但是曝光率低(广告不曝光，就拿不到收入)

4. 给媒体出高价：曝光率高，但是毛利额低。

所以在给媒体出价这个问题上，存在一个平衡，今天所说的“智能出价”，指的就是给媒体的出价，以达到我们的毛利额最大的效果，同时解放运营同事，提高他们的运营效率。

基础模型

由上述背景所述可知，毛利额的计算方式是简单的减法运算，平台成交价减去媒体成交价，但是我们又知道，广告如果不曝光，广告主是不会给我们支付费用的，所以如果仅仅从平台成交价和媒体出价两方面来考虑问题是不全面的，我们还要涉及到曝光率的问题。一般来说，我们可以根据曝光率来计算一条广告可能带来的毛利收入(期望最大化)，具体的计算方式如下：

价值函数= max( (平台成交价 - 媒体成交价) * 曝光率 )

这个函数所要表达的意思是：

1. 曝光率：针对历史数据，计算每一个出价(精确到个位数)的曝光率(可使用实时计算系统进行统计)

2. 媒体成交价：针对历史数据，计算每一个出价(精确到个位数)在媒体侧的成交价

3. (平台成交价 - 媒体成交价)：实际毛利额

4. (平台成交价 - 媒体成交价) * 曝光率：可以理解为毛利额的期望，当然此处的期望和数学上的期望有一定的差别。

上面这个价值函数就是最终出价的一个标准，哪个出价算出来的价值函数最大，就出那个价格。

初版开发

算法侧：以平台和广告位维度，使用实时计算系统flink计算过去两分钟内每个出价的曝光数α、未曝光数β、媒体侧平均成交价γ。形成如下的数据结构存储到redis集群：

key：平台_广告位

value：出价1：α，β，γ|出价2：α，β，γ|出价3：α，β，γ|出价4：α，β，γ|出价5：α，β，γ|...

服务侧：针对平台+广告位，从redis里面取出对应的value值，计算每一个出价的价值函数，取价值函数最大的出价作为最终给媒体的出价，我们的价值函数如下：

价值函数= max( (平台成交价 - 媒体成交价) * 曝光率 )

平台成交价：已知

媒体平均成交价：γ

曝光率：α / (α +β)

缺点：经过在线上实际业务场景中的实践发现，此类算法更容易倾向于给媒体出低价来获取更高的毛利额，原因在于我们的价值函数(毛利额 = 平台成交价 - 媒体成交价)，当我们出低价的情况下，毛利额能最大化。但是这里面显然涉及另外一个问题，就是出价低毛利额大，但是在媒体侧的曝光率会受到影响，这样我们根本拿不到一定的曝光规模，这也就是我最开始说的，低出价情况下毛利额高但是曝光率低的问题。为了解决这个问题，我们需要修改初始目标，将实现业务毛利额最大化改为在实现规模扩充的基础上的毛利额最大化。

后续改进方式：增加平台+广告位的底价调整系数，一来防止出价过低拿不到曝光，而来可以根据底价调整系数来动态调整最低的出价，达到毛利额最大化的目的。具体实施方案见下一章节。

底价调整系数

在上一章节中，我们提到为了解决总是给媒体出低价而拿不到曝光规模的问题，提出了增加”底价调整系数”的方案。这里所说的“底价调整系数”的实际含义其实就是最低出价的一个系数，比如：

如果我们的系数设置的是0.5，平台成交价是100元的话，我最低给媒体的出价是 100*0.5 = 50元，也就是说，50元以下的出价我不再考虑，针对价值函数，只计算50~100元之间最大的值，这样我们就尽量减少出低价，以此来提升我们的曝光率(也就是曝光规模)。

为了找到最好的底价调整系数，我们需要动态的调整底价系数，具体的实施方案如下：

实施策略：默认广告位-平台维度的底价系数为0.5，在策略启动时，优先使用0.5和0.6进行比较，若0.5比0.6更优（比较策略见定时任务），说明系数低的比较好，则比较0.4和0.5；若0.6更优，说明系数高的比较好，则比较0.6和0.7的效果；即每比较一次都会踢出效果较差的，若是系数数值比较低的最优，则后续对比值-0.1，若系数值高的最优，则后续对比值+0.1

定时任务：每小时计算该系数对应平台-广告位的媒体下发数，以及A\B两个系数下”曝光率提升比例”及”千次下发毛利的提升比例”,对比方式为：

1、当下发数 > 阈值(可配置)

-- 若A相对于B的曝光率提升比例及千次下发毛利提升比例都为正，则A比B好，否则B比A好

-- 若A相对于B，曝光率提升为正，千次下发毛利提升为负，则计算A曝光率提升比例/B千次下发毛利提 升比例>= 1，则A比B好，否则B比A好

2、当下发数 < 阈值

不做任何操作，继续累计，直到累计数大于阈值为止

媒体出价区间：【MAX（max(媒体底价，最小媒体出价)，min(平台成交价*返点*调整系数，最大媒体出价*调整系数)），MIN(平台成交价*返点，最大媒体出价)】

缺点：经过在线上实际业务场景中的实践发现，通过不断动态调整出价系数，线上会出现系数极端现象，当系数出现在0.8和0.9之间且一直是0.9系数曝光率和千次响应毛利表现较好时，系数则一直保持在0.8和0.9之间，此时若平台侧成交价较高，媒体侧出价也会变高，但出高价并未能影响到曝光率提升，反而毛利率下降明显（在媒体侧出60和出40对应的曝光率差不多，为何不出40？）

下一步优化策略：

1、还是要想办法去掉底价系数这个参数，根据实际的情况，让算法自动调节出价。

2、从当前进度看，此版本的千次下发毛利额的效果是最好的，因历史原因，此版本定义为V5版本，以后所有版本的演进效果，都以此版本为对照，以效果超过V5版本为目标。

3、之前计算曝光率的α，β值都是根据实际情况的曝光量和未曝光量累计得到的，通过实际的数据来看，不同的出价的曝光率出现参差不齐的现象，有可能高价的曝光率低于低价的曝光率，为了解决这个问题，我们针对曝光率的计算算法进行了改进，使之从理论上呈现出来一种递增效果，即：出价越高，曝光率越高。

曝光率优化

之前的曝光率是单点激励惩罚的机制进行更新，所谓单点激励惩罚指的是如果某个出价的情况下，广告曝光或者未曝光，只更新该出价的α，β值，但是经过进一步的思考认为，可以使用区间激励惩罚的机制进行更新，所谓的区间激励惩罚指的是，某个出价的情况下，广告曝光或者未曝光，不仅仅更新该出价的α，β值，对其他出价的α，β也做相应的惩罚和激励。

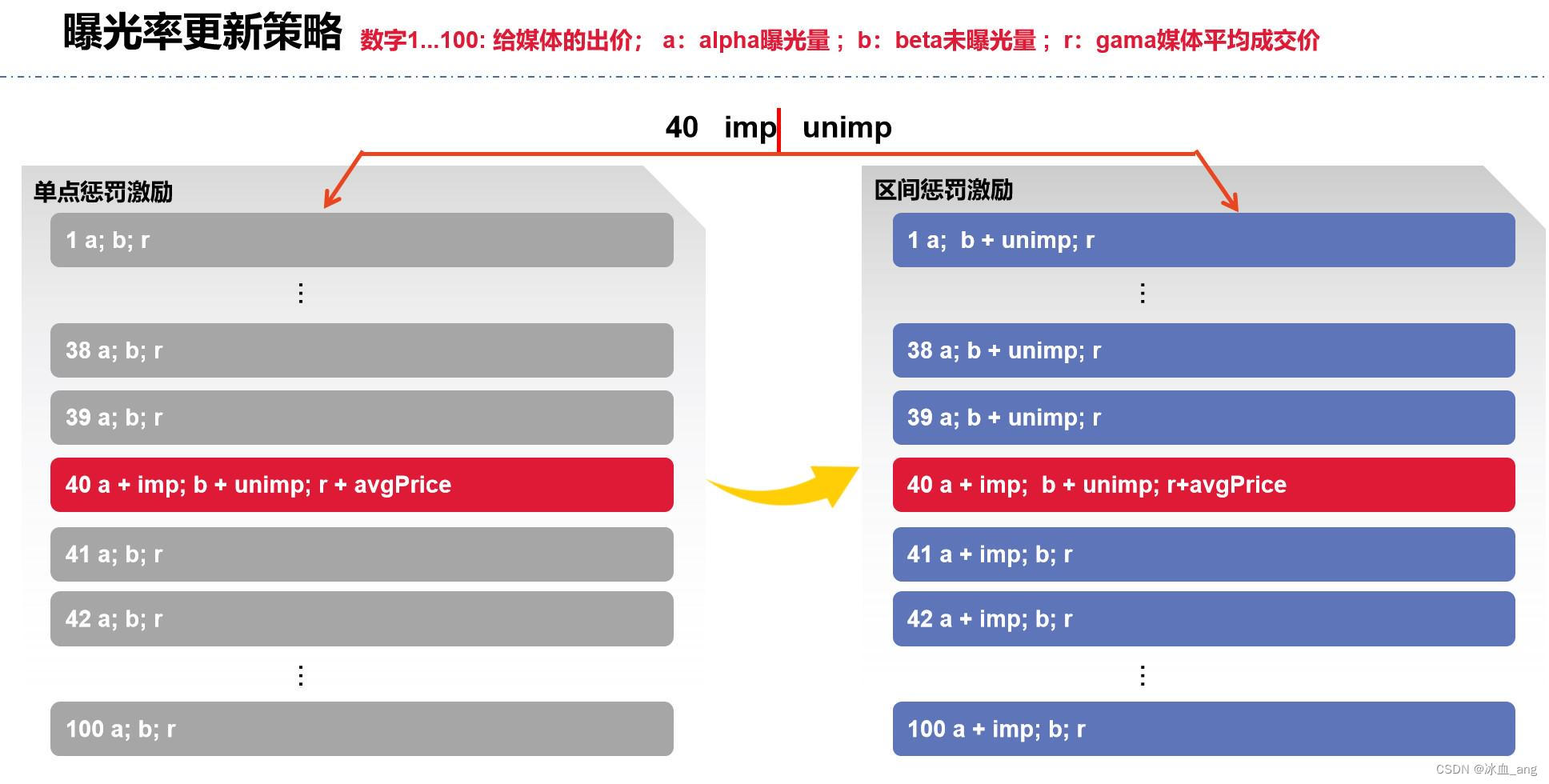
区间激励惩罚--第一次演进

在该次演进中，主要针对两种情况进行区间激励惩罚

情况1：如果某个出价未曝光，则小于这个出价的所有出价的β都进行更新：β + 1;而大于该出价的所有出价不进行更新。

情况2：如果某个出价曝光，则大于这个出价的所有出价的α都进行更新：α + 1;而小于该出价的所有出价不进行更新。

优点：解决了之前使之从理论上呈现出来一种递增效果，即：出价越高，曝光率越高。

缺点：使用这种更新方式，在高价部分的曝光率会出现一样的情况(如下图)，导致算法给出的价格比V5版本低的情况，为了解决这个问题，我们对区间激励惩罚机制进行了二次演进。

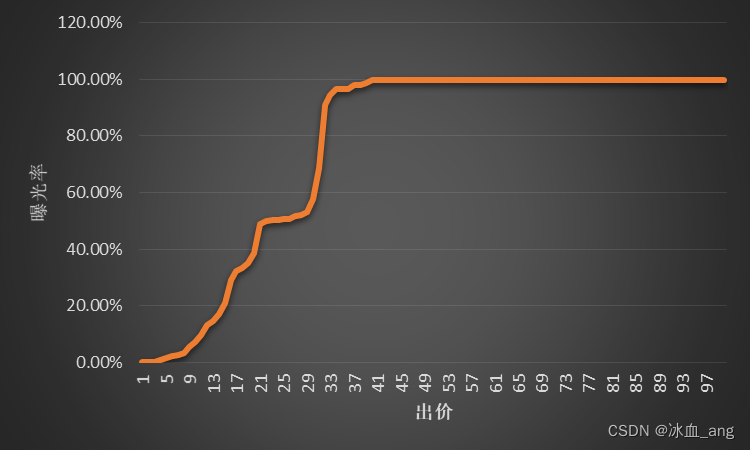
区间激励惩罚--第二次演进

为了解决第一次演进过程中，在高价部分曝光率一样的问题，进过进一步的思考和优化，认为在进行区间激励惩罚的过程中，针对不同的出价的激励惩罚程度应该是不一样的，具体来说，还是分为两种情况：

1、出价曝光的情况

(1)、高于该出价的出价：应该也会曝光，所以更新方式和第一次演进应该是一样的，即α + 1

(2)、低于该出价的出价：在第一次演进版本中，未对该部分进行更新。但是经过分析认为，如果当前价格曝光，则出价低于当前价格时，应该也有曝光的机会，所以对这一部分的出价，也应该给予一定的激励和惩罚，激励惩罚方式为：价格越低，α 更新越少，β更新越多，但总体α + β = 1

2、出价未曝光的情况

(1)、低于该出价的出价：应该也不会曝光，所以更新方式和第一次演进应该是一样的，即β + 1

(2)、高于该出价的出价：在第一次演进版本中，未对该部分进行更新。但是经过分析认为，如果当前价格未曝光，但出价高于当前价格时，应该有曝光的机会，所以对这一部分的出价，也应该给予一定的激励和惩罚，激励惩罚方式为：价格越高，α 更新越多，β更新越少，但α + β = 1

3、α，β更新方式

针对新的α，β更新方式，确定了两种形式，一种是对数函数的方式，一种是等比例方式。

经过模拟试验，这两种更新方式的最终的曝光率效果如下：

4、优点

解决了第一次曝光率演进过程中出现的高价部分曝光率未区分开的问题，使用这种针对不同出价进行不同程度的激励惩罚方式，再结合下一章中毛利额优化之后的函数，可以较好的解决高价出不上去的问题。

毛利额函数优化

为了便于描述，这里将价值函数再列一下：

价值函数= max( (平台成交价 - 媒体成交价) * 曝光率 )

可以看到在这个函数中，在计算价值函数的时，毛利额直接使用的是“平台成交价 - 媒体成交价”，用这种计算方式进行计算，有两个问题：

(1)、对于不同的媒体成交价(给媒体的出价)，他们的毛利额比值过大。

举个简单的例子，当平台成交价是100元时，出价10元，毛利额是90；出价90元，毛利额是10元，毛利额之间的差距是9倍，如果想要用90元进行出价，则90元的曝光率必须是10元的9倍，而这种程度的比例在曝光率中是很难拉回来的。

(2)、曝光率和毛利额的单位不对等的问题：曝光率的值始终是在0~1之间，而毛利额的值在0~100之间。

为了解决上述两个问题，想到一个解决办法，针对毛利额进行归一化处理，将毛利额也归一到0~1之间，同时缩小不同出价的毛利额之间的比例，使用对数函数的方式进行归一化处理，归一化函数如下：

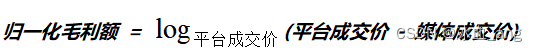
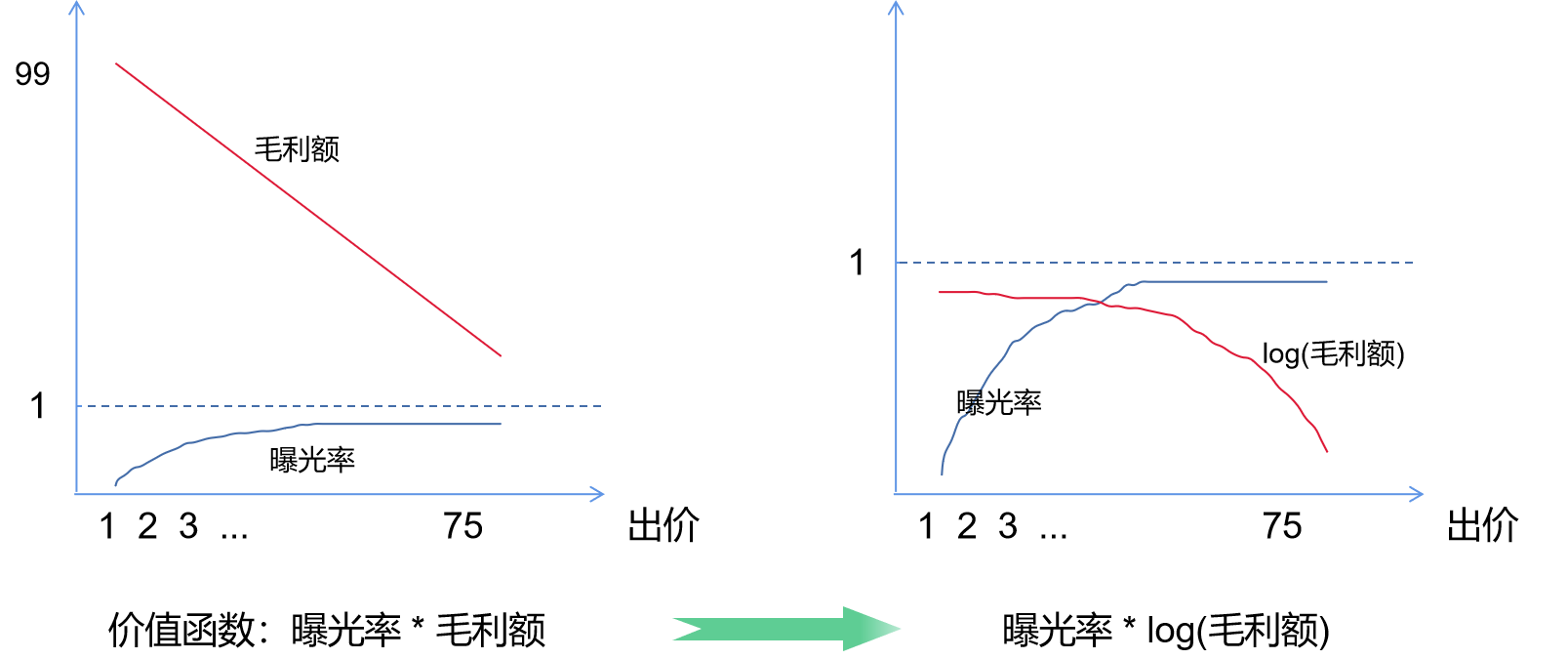
使用这种方式，就将之前的价值和函数变为：

价值函数= max( 归一化毛利额 * 曝光率 )

本地模拟程序构建

为了在上线之前看到实际的演进效果，在本地构建智能出价的模拟程序，目的有三：

1、针对提出的演进方式，进行本地模拟，观察曝光率及毛利额的最终效果是否如预期

2、观察出价能力能否赶上V5版本

3、本地模拟，减少不必要的上线流程，快速看到效果。

模拟效果：

经过多次模拟，线上运行之后的曝光率和本地模拟的情况完全一致，解决了不必通过上线，在本地模拟进行初步判断的方式，减少了或者避免了不必要的上线流程。

平台成交价分区间

通过上述方式的演进过程，在实际的在线测试中，出价能力总是稍逊于V5版本。举一个简单的例子，当平台成交价是10元的情况下，v5版本的出价维持在6元和7元，而我们的演进版本中，出价总是低于6元，为了了解具体原因进行了深入分析，这其中有两个主要的原因。

原因1：返点的问题

在实际的结算过程中，针对不同的DSP平台和广告位，我们会有不同的返点给予平台，在我们上述进行毛利额计算的情况下，是直接用平台成交价进行计算的：“平台成交价 - 媒体成交价”，但是实际上我们的毛利额应该是“平台成交价 * 返点系数 - 媒体成交价”，所以我们再次对价值函数进行了修正，如下：

价值函数= max( 归一化毛利额 * 曝光率 )

说明：在对数函数中+2的原因是，如果平台成交价10元，返点系数0.7的情况下，对数函数的底是7，value值是(7-媒体成交价)，在这种情况下，当出价是6元或者7元的情况下，归一化毛利额分别是0和负无穷，这种情况下，我们永远出不到6元和7元的价格，所以+2进行了一下修正。

原因2：用总体的曝光率掩盖了不同平台成交价曝光率的差异

到目前为止，针对同一平台和广告位，所使用的曝光率是总体情况的曝光率，什么意思呢？比如出价10元的曝光率是所有平台成交价在出10元情况下的曝光数据的累积数据。但是在实际情况下，平台成交价是20元和100元的情况下，出价10元的曝光率应该是不一样的，我们犯了一个用总体掩盖了个体特性的错误。

为了解决这个问题，我们针对不同的平台成交价，计算不同平台成交价下不同出价的曝光率，解决前后的曝光率计算方式如下所示：

解决前：

解决后：