一、离散傅立叶变换算法简要
给定一个N点的离散信号序列x(n),其中n表示时刻,n = 0, 1, 2, ..., N-1。
定义离散傅立叶变换的频域序列X(k),其中k表示频率,k = 0, 1, 2, ..., N-1。
通过以下公式计算每个频率对应的复数值:
X(k) = Σx(n) * exp(-j * 2π * kn / N),其中j表示虚数单位,exp表示指数函数。
上述公式中的指数函数是旋转因子,它表示每个频率对应的旋转角度。
重复步骤3,计算所有频率对应的复数值,得到频域序列X(k)。
最终得到的频域序列X(k)表示了原始信号在不同频率上的能量分布。
二、离散傅立叶变换的实现
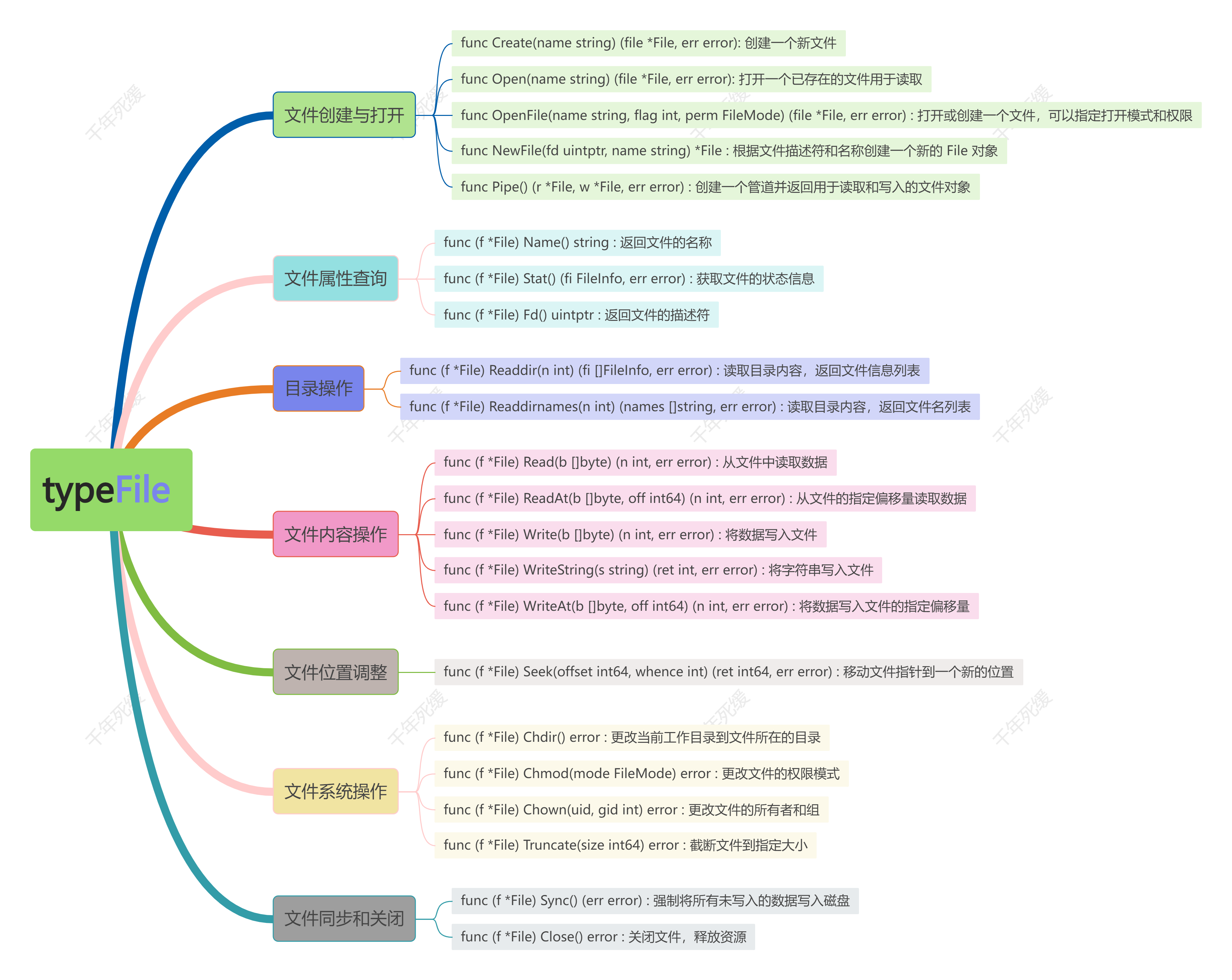
一维离散傅立叶变换函数 ,其调用格式与功 能为:(1) fft(X):返回向量 X 的离散傅立叶变换。设 X 的长度 ( 即元素个数 ) 为 N ,若 N 为 2 的幂 次,则为以 2 为基数的快速傅立叶变换,否 则为运算速度很慢的非 2 幂次的算法。对于 矩阵 X , fft(X) 应用于矩阵的每一列。(2) fft(X,N) :计算 N 点离散傅立叶变换。它限 定向量的长度为 N ,若 X 的长度小于 N ,则 不足部分补上零;若大于 N ,则删去超出 N 的那些元素。对于矩阵 X ,它同样应用于矩 阵的每一列,只是限定了向量的长度为 N 。(3) fft(X,[],dim) 或 fft(X,N,dim) :这是对于矩 阵而言的函数调用格式,前者的功能与 FFT(X) 基本相同,而后者则与 FFT(X,N) 基 本相同。只是当参数 dim=1 时,该函数作用 于 X 的每一列;当 dim=2 时,则作用于 X 的 每一行。 值得一提的是,当已知给出的样本数 N0 不是 2 的幂次时,可以取一个 N 使它大于 N0 且是 2 的幂次,然后利用函数格式 fft(X,N) 或 fft(X,N,dim) 便可进行快速傅立叶变换。这样,计算速度将大大加快。 相应地,一维离散傅立叶 逆变换 函数是 ifft 。 ifft(F) 返回 F 的一维离散傅立叶逆变换; ifft(F,N) 为 N 点逆变换; ifft(F,[],dim) 或 ifft(F,N,dim) 则由 N 或 dim 确定逆变换的点数或操作方向。
例
6-15
给定数学函数
x(t)=12sin(2
π×
10t+
π
/4)+5cos(2
π×
40t)
取
N=128
,试对
t
从
0~1
秒采样,用
fft
作快速傅
立叶变换,绘制相应的振幅
-
频率图。
在
0~1
秒时间范围内采样
128
点,从而可以确
定采样周期和采样频率。由于离散傅立叶
变换时的下标应是从
0
到
N-1
,故在实际应
用时下标应该前移
1
。又考虑到对离散傅立
叶变换来说,其振幅
| F(k)|
是关于
N/2
对称
的,故只须使
k
从
0
到
N/2
即可。
程序如下:
N=128; % 采样点数
T=1; % 采样时间终点
t=linspace(0,T,N); % 给出N个采样时间ti(I=1:N)
x=12*sin(2*pi*10*t+pi/4)+5*cos(2*pi*40*t); % 求各采样点 样本值x
dt=t(2)-t(1); % 采样周期
f=1/dt; % 采样频率(Hz)
X=fft(x); % 计算x的快速傅立叶变换X
F=X(1:N/2+1); % F(k)=X(k)(k=1:N/2+1)
f=f*(0:N/2)/N; % 使频率轴f从零开始
plot(f,abs(F),'-*') % 绘制振幅-频率图
xlabel('Frequency');
ylabel('|F(k)|')运行结果 :

![]() 结语
结语
一口吃不成胖子
但胖子却是一口一口吃来的
!!!