作者:非妃是公主
专栏:《算法》《刷题笔记》
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
《算法》专栏系列文章
算法设计与分析复习01:主方法求递归算法时间复杂度
算法设计与分析复习02:分而治之算法
算法设计与分析复习03:动态规划算法
算法设计与分析复习04:贪心算法算法设计与分析复习05:回溯及分支限界
算法设计与分析复习06:随机化算法
算法设计与分析复习07:样题
文章目录
- 《算法》专栏系列文章
- 题目:寻友之旅
- 贪心算法
- 宽度优先搜索(bfs)
- bfs+剪枝
- 考虑特殊情况(无法坐公交)
- 测试结果
题目:寻友之旅
小青要找小码去玩,他们的家在一条直线上,当前小青在地点 N ,小码在地点 K (0≤N , K≤100 000),并且小码在自己家原地不动等待小青。小青有两种交通方式可选:步行和公交。
步行:小青可以在一分钟内从任意节点 X 移动到节点 X-1 或 X+1
公交:小青可以在一分钟内从任意节点 X 移动到节点 2×X (公交不可以向后走)
请帮助小青通知小码,小青最快到达时间是多久?
输入: 两个整数 N 和 K
输出: 小青到小码家所需的最短时间(以分钟为单位)
贪心算法
首先,可以分析下这道题目!我第一个想法是,这是1个贪心的题目,每一步我们可以选择不同的走法,即:
- -1:向后走
- +1:项前走
- *2:坐公交去走
有了这3种走法后,那么哪种走法是最优的呢?我使用了距离终点点的距离(也就是K的距离)来度量,每次选择离K最近的走法,代码如下,十分简单,读者可以根据我上面说的自行理解即可:
// 方法1:贪心算法
int main() {
int N, K;
cin >> N >> K;
int num_step = 0;
while (N != K) {
num_step++;
int plan1 = N - 1;
int plan2 = N + 1;
int plan3 = 2 * N;
if (plan1 < 0 || plan1 > 100000) plan1 = N;
if (plan2 < 0 || plan2 > 100000) plan1 = N;
if (plan3 < 0 || plan3 > 100000) plan1 = N;
int len1 = abs(plan1 - K);
int len2 = abs(plan2 - K);
int len3 = abs(plan3 - K);
if (len1 > len2) {
if (len3 > len2) {
N = plan2;
}
else {
N = plan3;
}
}
else {
if (len3 > len1) {
N = plan1;
}
else {
N = plan3;
}
}
}
cout << num_step;
}
但是,这种做法其实是错误的,问题的产生主要是由于可以坐公交产生的,有时候我们这一步是最优的,从下一步来讲,就不一定是最优的。比如:
小青在5
小码在8
最优的走法是,小青先走到4,然后坐公交直接到8,这样只需要2分钟,但是这种做法是无法被贪心算法搜索到的。
宽度优先搜索(bfs)
接着我仔细思考了另一种做法,也就是bfs,bfs就是使用了队列这个数据结构,进行一个宽度优先搜索。但是如何记录当前的分钟数是1个问题,因此,我定义了1个结构体,然后就是出队列、入队列等操作,代码如下:
// 方法2:bfs
struct node {
int num_steps;
int pos;
};
int main() {
int N, K;
cin >> N >> K;
queue<node> que;
node curNode;
curNode.num_steps = 0;
curNode.pos = N;
que.push(curNode);
while (curNode.pos != K) {
node tmp1;
tmp1.num_steps = curNode.num_steps + 1;
tmp1.pos = curNode.pos - 1;
node tmp2;
tmp2.num_steps = curNode.num_steps + 1;
tmp2.pos = curNode.pos + 1;
node tmp3;
tmp3.num_steps = curNode.num_steps + 1;
tmp3.pos = curNode.pos * 2;
if (tmp1.pos >= 0 || tmp1.pos <= 100000)
que.push(tmp1);
if (tmp2.pos >= 0 || tmp2.pos <= 100000)
que.push(tmp2);
if (tmp3.pos >= 0 || tmp3.pos <= 100000)
que.push(tmp3);
curNode = que.front();
que.pop();
}
cout << curNode.num_steps;
}
代码也较为简单,虽然没有注释,但是并不难看懂,读者可以根据我上面提到的代码逻辑进行理解。
bfs+剪枝
但是,bfs的搜索空间其实是很大的,对于题目的数据0~100000,可能会造成较大的时间、空间开销。因此,可以对代码进行进一步的剪枝,主要是融入一些启发式的思考,排除掉肯定不可能的情况,我主要排除了下面这种情况:如果小青已经超过了小码,而且小青距离小码的距离,比上一步还远,那么这种情况的后续步骤肯定不存在最优解了,因为这样走的话,我们越走越远,在无效地浪费时间!
我举个例子,比如,小青在600处,小码在800处,如果小青坐公交,那么直接就到了1200处,这样的话,小青距离小码有400,而上一步小青距离小码只有200,关键是400的距离还不能坐公交(只能走着回去),所以这肯定不是最优解!因此我改动的代码如下:
if (tmp3.pos >= 0 || tmp3.pos <= 100000 || tmp3.pos - K < abs(curNode.pos - K))
que.push(tmp3);

考虑特殊情况(无法坐公交)
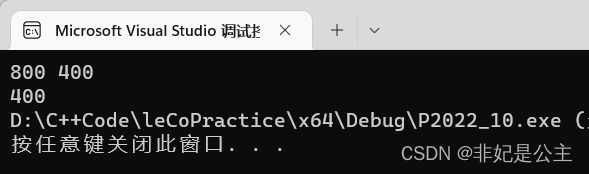
对于某些特殊情况,比如小青在800,小码在400,这时候是无法乘坐公交的,当然做法也很简单,就是二者之间的距离。
为什么要考虑这种特殊情况呢?因为不考虑这种情况的话,对于上面的这种情况,bfs的搜索空间是
2
400
2^{400}
2400,一共要扩展400层搜索树,这是很恐怖的!因此增加代码如下:

完整代码如下:
struct node {
int num_steps;
int pos;
};
int main() {
int N, K;
cin >> N >> K;
if (N > K) {
cout << N - K;
return 0;
}
queue<node> que;
node curNode;
curNode.num_steps = 0;
curNode.pos = N;
que.push(curNode);
while (curNode.pos != K) {
node tmp1;
tmp1.num_steps = curNode.num_steps + 1;
tmp1.pos = curNode.pos - 1;
node tmp2;
tmp2.num_steps = curNode.num_steps + 1;
tmp2.pos = curNode.pos + 1;
node tmp3;
tmp3.num_steps = curNode.num_steps + 1;
tmp3.pos = curNode.pos * 2;
if (tmp1.pos >= 0 || tmp1.pos <= 100000)
que.push(tmp1);
if (tmp2.pos >= 0 || tmp2.pos <= 100000)
que.push(tmp2);
if (tmp3.pos >= 0 || tmp3.pos <= 100000 || tmp3.pos - K < abs(curNode.pos - K))
que.push(tmp3);
curNode = que.front();
que.pop();
}
cout << curNode.num_steps;
}
测试结果
- 测试用例1:K=5,N=8,需要2分钟,输出如下:
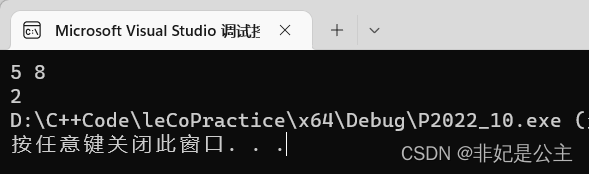
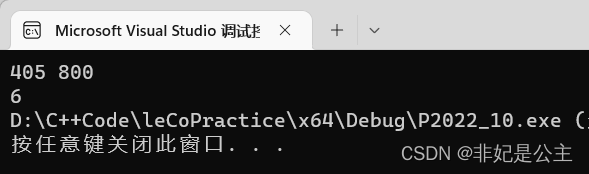
- 测试用例2:K=405,N=800,需要6分钟,输出如下:
- 测试用例3:K=800,N=400,这个因为无法乘坐公交,只能步行,因此需要400分钟,输出如下: