搜索算法基础

一 DFS

深度优先搜索算法（Depth First Search，简称DFS）：一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。
这个算法一开始仅仅只是图还有树这种数据结构的遍历方法，但是这种方法可以用来搜索，枚举一个问题的所有解，因为求出一个问题的解的过程就是一个层次递进的过程。下面就用全排列举一个例子：
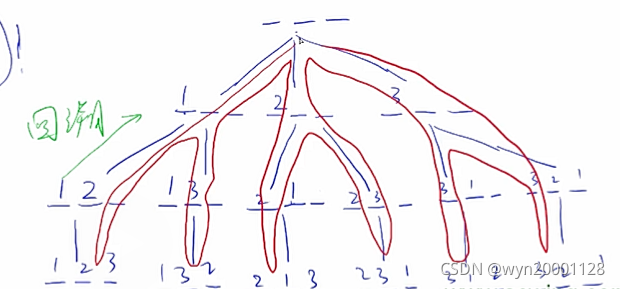
在这里插入图片描述
全排列的所有解都可以看成一个叶子节点。全排列的第一个数字就是树的第一层，因此可见DFS递归函数都是从0开始的，这样代表搜索从这个解空间的树的根节点开始。搜到树的叶子节点的时候就回溯，回溯的同时要记得恢复现场。下面是一个全排列用DFS来解的代码：
下面是几个经典问题的代码：
（1）全排列（搜索范围是n大小的数组，策略就是每一次搜出一个数）

#include <iostream>
using namespace std;
const int N=10 ;
int path[N];
bool array[N];
int n;//这个n要设置为全局变量，因为这是判断十分搜索到叶子节点的关键
void dfs(int u)
{   int i;
	if(u==n) {//判断此时的递归是否已经搜到叶子节点
		for(i=0;i<n;i++) printf("%d",path[i]);
		printf("\n");
		return;//搜索到叶子节点的时候结束递归 
	}
	
	for(i=1;i<=n;i++) //遍历所有可能情况
	{
		if(!array[i])//满足条件就存进结果
		{
			path[u]=i;
			array[i]=true;//做DFS的时候要有两个结构，一个用来记录状态，一个用来存储搜索的结果
			dfs(u+1);//继续往下搜索 
			array[i]=false;//回溯的时候还原现场，就写在递归调用的后面
		}
	}
	
}
int main(int argc, char** argv) {
	cin>>n;
	dfs(0);//表示从根节点开始搜索
	return 0;
}

（2）八皇后问题（策略是按行来搜索，一行一行找一个合法的）

#include <iostream>
using namespace std;
const int N = 20; 

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u) {
    // u == n 表示已经搜了n行，故输出这条路径
    if (u == n) {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   // 等价于cout << g[i] << endl;
        puts("");  // 换行
        return;
    }

    //对n个位置按行搜索
    for (int i = 0; i < n; i ++ )
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        // udg[n - u + i]，+n是为了保证下标非负
        if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
            g[u][i] = '.';

        }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}

（3）小猫爬山（策略是一只一只小猫安排，直到安排完为止）
翰翰和达达饲养了 N 只小猫，这天，小猫们要去爬山。经历了千辛万苦，小猫们终于爬上了山顶，但是疲倦的它们再也不想徒步走下山。翰翰和达达只好花钱让它们坐索道下山。索道上的缆车最大承重量为 W，而 N 只小猫的重量分别是 C1、C2……CN。当然，每辆缆车上的小猫的重量之和不能超过 W。每租用一辆缆车，翰翰和达达就要付 1 美元，所以他们想知道，最少需要付多少美元才能把这 N 只小猫都运送下山？
代码如下：

#include <algorithm>
#include <iostream>
using namespace std;
const int N = 2e1;
int cat[N];//用于存储每一只小猫的重量
int cab[N];//用于所有缆车剩余的空间
int n, w;
int ans;
bool cmp(int a, int b) {
    return a > b;
}
void dfs(int now, int cnt)//两个参数，now表示当前要分配的小猫是第now个，cnt表示目前已经分配的缆车数量
{
    if (cnt >= ans) {
      return;//这是一个剪枝的过程，因为要求的是最小的，
             //所以在搜索的过程种如果比之前搜索的ans要大直接不用搜索了
    }
    if (now == n + 1) {
        ans = min(ans, cnt);
        return;
    }
    //尝试分配到已经租用的缆车上
    for (int i = 1; i <= cnt; i++) {  //分配到已租用缆车
        if (cab[i] + cat[now] <= w) {//表示分配到可以组用的缆车上去
            cab[i] += cat[now];
            dfs(now + 1, cnt);
            cab[i] -= cat[now];  //还原
        }
    }
    // 新开一辆缆车
    cab[cnt + 1] = cat[now];
    dfs(now + 1, cnt + 1);
    cab[cnt + 1] = 0;//还原
}

int main() {
    cin >> n >> w;
    for (int i = 1; i <= n; i++) {
        cin >> cat[i];
    }

    sort(cat + 1, cat + 1 + n, cmp);

    ans = n;

    dfs(1, 0);

    cout << ans << endl;

    return 0;
}

DFS的模板如下：

void dfs()//参数用来表示状态
{
    if(到达终止状态)//递归出口
    {
        ...//根据题意来添加
        return；
    }

    if(越界或者不合法状态)
        return;//可以用于剪枝
    else
    {
        for(扩展方式)
        {
            if(扩展方式所达到的合法状态)
            {
                ...//根据题意来添加
                vis[i]=1;//表示已经操作过了
                dfs();
                vis[i]=0;//还原操作
            }
        }
    }
}

for循环是用来遍历所有拓展的方式（例如全排列当中所有的数字），而后写一个if语句判断情况是否可以拓展，如果情况满足条件就进行对应的操作和下层递归调用，递归调用完之后要还原现场。

     for(扩展方式)
        {
            if(扩展方式所达到的合法状态)
            {
                ...//根据题意来添加
                vis[i]=1;//标记
                修改（剪枝）
                dfs();
                vis[i]=0;
                //是否还原标记根据题意来
                //如果加上还原标记，就是回溯算法
            }
        }

通过这3个例子我们可以看出如果要做DFS题目的话一定要确定一个“搜索空间”。例如全排列是一个大小为n的数组，n皇后问题是原有的二维数组，小猫上山就是那个小猫数组。在这个覆盖全局的搜索空间制定搜索策略来找出符合条件的情况就是DFS编程的思路，而这样的搜索过程是一定可以枚举出所有可能性的。

二 BFS

宽度优先搜索算法（又称广度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。BFS的搜索还有一个性质：BFS搜出来的结果一定是“最短的”
说通俗一点，以下面一个问题为例子：
给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。
最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。接下来 n 行，每行包含 m 个整数（0 或 1），表示完整的二维数组迷宫。目的是输出一个整数，表示从左上角移动至右下角的最少移动次数。
输入样例：
$\; 1\; 0\; 0\; 0\\ 0\; 1\; 0\; 1\; 0\\ 0\; 0\; 0\; 0\; 0\\ 0 \; 1\; 1 \; 1\; 0\\ 0 \; 0\; 0\; 1 \; 0$
代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e2 + 7;
int g[N][N], d[N][N];
int n, m;
int bfs() {
    int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
    queue <PII> q;
    for (auto &v : d) 
        for (auto &x : v) {
            x = - 1;
        }
    d[0][0] = 0;
    q.push({0, 0});
    while (!q.empty()) {
        auto t = q.front();
        q.pop();
        for (int i = 0; i < 4; i++) {
            int x = t.first + dx[i], y = t.second + dy[i];
            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
                d[x][y] = d[t.first][t.second]  + 1;
                q.push({x, y});
            }
        }

    }
        return d[n - 1][m - 1];
}
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }

    cout << bfs() << endl;

    return 0;
}

从代码可以知道BFS的步骤就是：
①把初始状态（起点）放到队列中。
②把起点搜索到的结果放入队列并记录结果，而后把起点出队列。
③执行与②相似的操作：把stage为i-1的结果出队列，把stage为i的结果入队列。（再题目中表示为把距离原点i-1的位置出队列，把距离原点i的位置入队列）。
④当搜索结果达到边界条件的时候就不会再有搜索的结果入队列了，而又有结果出队列，所以当队列为空的时候循环就结束了。
这个步骤可以使用一个循环写出来，这个while循环过程可以根据以下准则划分成若干阶段：把stage为i-1的所有结果出队列，把stage为i的所有结果入队列，并且一个结果出队列以后就有一个结果入队列。（注意是所有结果）。