Kendo UI致力于新的开发，来满足不断变化的需求。现在我们非常自豪地宣布，通过React框架的Kendo UI JavaScript封装来支持React Javascript框架。KendoReact能够为客户提供更好的用户体验，并且能够更快地构建更好的应用程序。

理想情况下，日期选择工具应该完全无摩擦，以至于用户根本不会注意到它们的存在。如果用户主动注意到一个日期范围选择工具，那可能是它出了问题。好的设计都是无形的，但不能用因为客户不考虑，我们开发人员也忽视它。

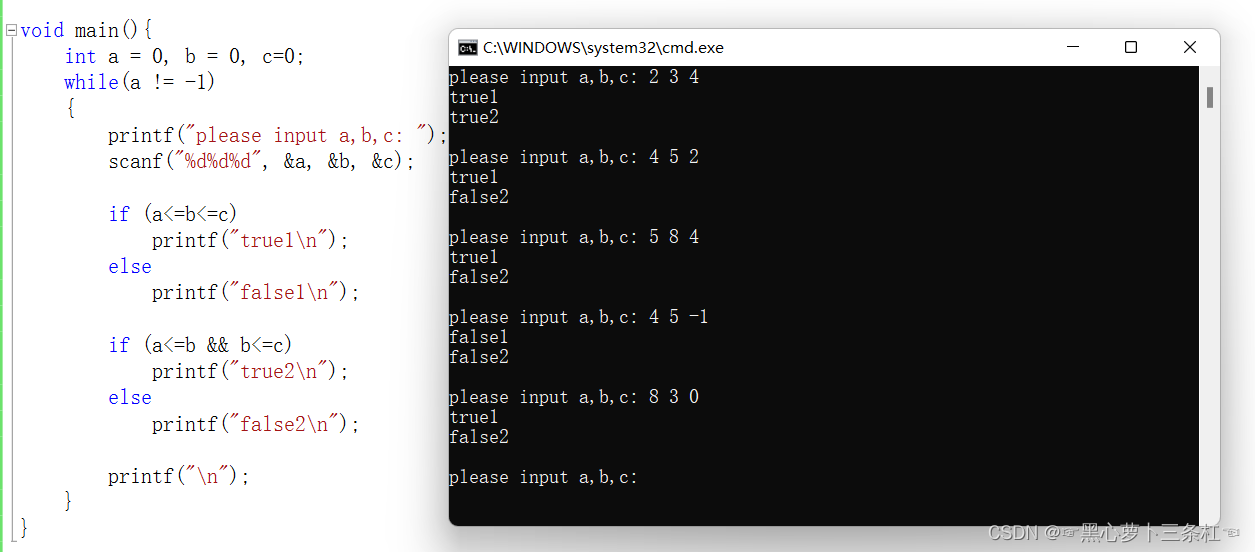
Kendo UI R3 2022正式版下载(Q技术交流：726377843）

KendoReact中的DateRangePicker React组件是一种工具，可以快速轻松地选择一系列日期。它也是一个高度可定制的组件，提供了出色的用户体验和出色的开发人员体验，同时拥有多种自定义外观和操作选项，包括最小和最大日期、默认值、禁用日期等。

功能

Date Range Picker组件的功能非常丰富，它包含了开发人员所期望的功能：验证、默认值等……但它还包括高级功能(例如反向选择和完整的键盘支持)，这些功能不是在任何组件中都能找到的。

反向日期选择和日期交换

大多数情况下，当处理日期范围选择时，我们假设结束日期将在开始日期之后。但有时候也会有不同，需要用户能够选择结束日期在开始日期之前的日期。

幸运的是，DateRangePicker组件使它变得简单！只需将allowReverse属性设置为true，就可以开始了！除了反向选择逻辑，还可以呈现一个按钮来交换开始日期和结束日期值，要显示交换按钮，将swapButton和allowReverse属性都设置为true。这将在日期输入框之间添加一个新按钮，允许用户快速来回切换所选的开始和结束日期，只需单击一下!

自定义和样式

DateRangePicker(以及所有KendoReact组件)也非常容易自定义样式。

开发人员可以将以下DateRangePicker组件替换为自定义组件：

• 开始和结束日期输入，它呈现DateRangePicker的开始和结束范围选择的输入

• 日历，在DateRangePicker的弹出窗口中呈现MultiViewCalendar

• 弹出窗口，它呈现包含MultiViewCalendar的弹出框

这允许用户创建一个真正独特和个性化的用户体验，此外DateRangePicker还支持完整的主题支持，因此无论您使用什么设计系统，都可以轻松匹配应用程序的外观和感觉！组件可以通过KendoReact内置主题(Material, Fluent, Bootstrap和默认主题)，自定义CSS或ThemeBuilder轻松实现主题化。

可访问性

当谈到输入工具时，可访问性绝对是至关重要的……然而，这是自己很难实现的，而且通常是其他组件库所缺乏的。

KendoReact DateRangePicker包括完整的可访问性支持，使所有的用户都可以轻松地导航您的应用程序。它有一个内置的role和aria-label属性，并提供完整的键盘导航支持。aria-valuemin、aria-valuemax和aria-valuenow属性定义了当用户输入值或与DateRangePicker交互时的可访问性值，它还遵循WAI-ARIA为其组件角色实现键盘导航的最佳实践，并且已经用几个流行的屏幕阅读器进行了测试。

DateRangePicker组件是一个重要的工具，可以在React应用程序中快速轻松地选择一系列日期。其广泛的功能和可定制选项确保了良好的用户体验，其全面的可访问性支持意味着每个人都可以直观地使用它。凭借其先进的功能和功能，它是一个强大的输入工具，可以让人感觉简单。