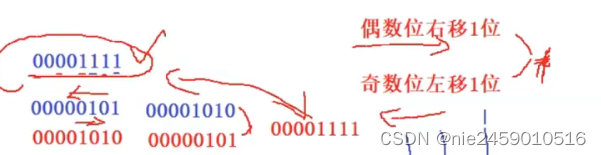
-
正则化 所有损害优化的方法都是正则化。增加优化约束,干扰优化过程
-
优化约束包括 L1/L2约束,数据增强
-
干扰优化包括 随机梯度下降 权重衰减 提前停止

在上式中 y ( n ) 为样本 n ,其展开形式为 y^{(n)}为样本n,其展开形式为 y(n)为样本n,其展开形式为,其中 n n n为第n个样本,N+1是样本的维度
y ( n ) = [ y 1 ( n ) y 2 ( n ) y 3 ( n ) . . . y N + 1 ( n ) ] (3) y^{(n)} = \left[ \begin{matrix} y_1^{(n)} \\ y_2^{(n)} \\ y_3^{(n)} \\ . \\ . \\ . \\ y_{N+1}^{(n)} \end{matrix} \right] \tag{3} y(n)= y1(n)y2(n)y3(n)...yN+1(n) (3)
x N + 1 ( n ) x^{(n)}_{N+1} xN+1(n)的维度是N+1,是第n组输入的样本
x N + 1 ( n ) = [ x 1 ( n ) x 2 ( n ) x 3 ( n ) . . . x N + 1 ( n ) ] (3) x^{(n)}_{N+1} = \left[ \begin{matrix} x_1^{(n)} \\ x_2^{(n)} \\ x_3^{(n)} \\ . \\ . \\ . \\ x_{N+1}^{(n)} \end{matrix} \right] \tag{3} xN+1(n)= x1(n)x2(n)x3(n)...xN+1(n) (3)w = [ w 1 ( n ) w 2 ( n ) w 3 ( n ) . . . w N + 1 ( n ) ] (3) w=\left[ \begin{matrix} w_1^{(n)} \\ w_2^{(n)} \\ w_3^{(n)} \\ . \\ . \\ . \\ w_{N+1}^{(n)} \end{matrix} \right] \tag{3} w= w1(n)w2(n)w3(n)...wN+1(n) (3)
w T = [ w 1 ( n ) w 2 ( n ) w 3 ( n ) . . . w N + 1 ( n ) ] (3) w^T=\left[ \begin{matrix} w_1^{(n)} & w_2^{(n)} & w_3^{(n)} & . & . & . & w_{N+1}^{(n)} \end{matrix} \right] \tag{3} wT=[w1(n)w2(n)w3(n)...wN+1(n)](3)