鲁棒无范围定位算法（RRGA）（Matlab代码实现）

news2025/1/13 13:22:16

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

估值的抗异常误差能力可以用影响函数定量分析.影响函数反映了不同位置上的异常数据对估值造成的相对影响,其绝对值越小,抗差能力越强[11].式(11)所示的广义M估计准则的影响函数为：

📚2 运行结果

部分代码：

scatter3(data(:,1), data(:,2), data(:,3), 5, data(:,3), 'filled');
colormap(gray);

% Calculate the eigenvectors and eigenvalues
covariance = cov(data);
tt1=data(:,1)-avg(1);tt2=data(:,2)-avg(2);tt3=data(:,3)-avg(3);
tt=[tt1 tt2 tt3];

cc=1/333*(transpose(tt)*tt);
[eigenvec, eigenval ] = eig(covariance);

% Get the index of the largest eigenvector
largest_eigenvec = eigenvec(:, 3);
largest_eigenval = eigenval(3,3);
medium_eigenvec = eigenvec(:, 2);
medium_eigenval = eigenval(2,2);
smallest_eigenvec = eigenvec(:, 1);
smallest_eigenval = eigenval(1,1);

% Plot the eigenvectors
hold on;
quiver3(X0, Y0, Z0, largest_eigenvec(1)*sqrt(largest_eigenval), largest_eigenvec(2)*sqrt(largest_eigenval), largest_eigenvec(3)*sqrt(largest_eigenval), '-m', 'LineWidth',3);
quiver3(X0, Y0, Z0, medium_eigenvec(1)*sqrt(medium_eigenval), medium_eigenvec(2)*sqrt(medium_eigenval), medium_eigenvec(3)*sqrt(medium_eigenval), '-g', 'LineWidth',3);
quiver3(X0, Y0, Z0, smallest_eigenvec(1)*sqrt(smallest_eigenval), smallest_eigenvec(2)*sqrt(smallest_eigenval), smallest_eigenvec(3)*sqrt(smallest_eigenval), '-r', 'LineWidth',3);
hold on;

% Set the axis labels
hXLabel = xlabel('x');
hYLabel = ylabel('y');
hZLabel = zlabel('z');
xlim([-10,10]);
ylim([-10,10]);
zlim([-10,10]);
title('Original 3D data');

%%%%%%%%%%%%% CENTER THE DATA %%%%%%%%%%%
data = data-repmat(avg, size(data, 1), 1);

%%%%%%%%%%%%% NORMALIZE THE DATA %%%%%%%%%%%
stdev = sqrt(diag(covariance));
data = data./repmat(stdev', size(data, 1), 1);

%%%%%%%%%%%%% DECORRELATE THE DATA %%%%%%%%%%%
decorrelateddata = (data*eigenvec);

% Plot the decorrelated data
figure;
scatter3(decorrelateddata(:,1), decorrelateddata(:,2), decorrelateddata(:,3), 5, decorrelateddata(:,3), 'filled');
colormap(gray);

% Plot the eigenvectors (which are now the axes (0,0,1), (0,1,0), (1,0,0)
% and the mean of the centered data is at (0,0,0)
hold on;
quiver3(0, 0, 0, 0, 0, 1*sqrt(largest_eigenval), '-m', 'LineWidth',3);
quiver3(0, 0, 0, 0, 1*sqrt(medium_eigenval), 0, '-g', 'LineWidth',3);
quiver3(0, 0, 0, 1*sqrt(smallest_eigenval), 0, 0, '-r', 'LineWidth',3);
hold on;

% Set the axis labels
hXLabel = xlabel('x');
hYLabel = ylabel('y');
hZLabel = zlabel('z');
xlim([-5,5]);
ylim([-5,5]);
zlim([-5,5]);
title('Decorrelated 3D data');

%%%%%%%%%%%%% PROJECT THE DATA ONTO THE 2 LARGEST EIGENVECTORS %%%%%%%%%%%

eigenvec_2d=eigenvec(:,2:3);

data_2d = data*eigenvec_2d;

% Plot the 2D data
figure;
scatter(data_2d(:,1), data_2d(:,2), 5, data(:,3), 'filled');
colormap(gray);

% Plot the eigenvectors
hold on;
quiver(0, 0, 0*sqrt(largest_eigenval), 1*sqrt(largest_eigenval), '-m', 'LineWidth',3);
quiver(0, 0, 1*sqrt(medium_eigenval), 0*sqrt(medium_eigenval), '-g', 'LineWidth',3);
hold on;

% Set the axis labels
hxLabel = xlabel('x');
hyLabel = ylabel('y');
ylim([-5,5]);
ylim([-5,5]);
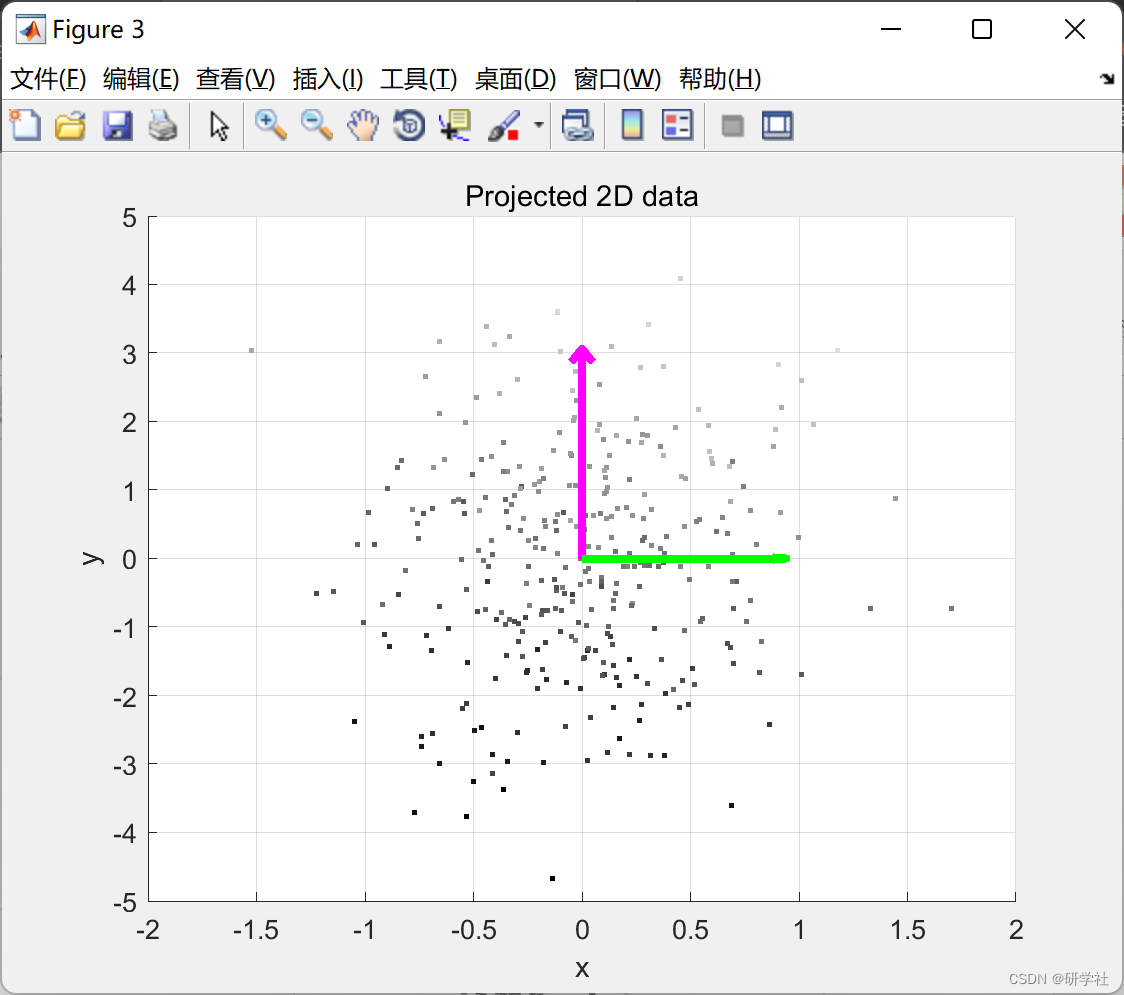
title('Projected 2D data');
grid on;

%%%%%%%%%%%%% PROJECT THE DATA ONTO THE LARGEST EIGENVECTOR %%%%%%%%%%%

eigenvec_1d=eigenvec(:,3);

data_1d = data*eigenvec_1d;

% Plot the 1D data
figure;
scatter(repmat(0, size(data_1d,1), 1), data_1d, 5, data(:,3), 'filled');
colormap(gray);

% Plot the eigenvector
hold on;
quiver(0, 0, 0*sqrt(largest_eigenval), 1*sqrt(largest_eigenval), '-m', 'LineWidth',3);
hold on;

% Set the axis labels
hXLabel = xlabel('x');
hYLabel = ylabel('y');
xlim([-5,5]);
ylim([-5,5]);
title('Projected 1D data');
grid on;