微分方程是物理科学的主角之一,在工程、生物、经济甚至社会科学中都有广泛的应用。粗略地说,它们告诉我们一个量如何随时间变化(或其他参数,但通常我们对时间变化感兴趣)。我们可以了解人口、股票价格,甚至某个社会对某些主题的看法如何随时间变化。
通常,用于解决微分方程的方法不是分析性的(即没有解决方案的“封闭公式”),我们必须利用数值方法。然而,从计算的角度来看,数值方法可能很昂贵,更糟糕的是:累积误差可能非常大。
本文将展示神经网络如何成为解决微分方程的宝贵盟友,以及我们如何借用物理信息神经网络的概念来解决这个问题:我们可以使用机器学习方法来解决微分方程吗?

NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
1、物理学信息神经网络
在本节中,我将简要介绍物理学信息神经网络(PINN)。我想你知道“神经网络”部分,但是是什么让它们受到物理学的影响?好吧,它们并不是完全由物理学决定的,而是由(微分)方程决定的。
通常,神经网络经过训练可以找到模式并弄清楚一组训练数据发生了什么。但是,当你训练神经网络遵循训练数据的行为并希望拟合看不见的数据时,你的模型高度依赖于数据本身,而不是系统的底层性质。这听起来几乎像一个哲学问题,但它比这更实际:如果你的数据来自对洋流的测量,这些洋流必须遵循描述洋流的物理方程。但是请注意,你的神经网络对这些方程完全不可知,并且只试图拟合数据点。
这就是物理学信息发挥作用的地方。如果你的模型除了学习如何拟合数据之外,还学习如何拟合控制该系统的方程,那么你的神经网络的预测将更加精确,并且泛化能力会更好,这只是物理信息模型的一些优点。
请注意,系统的控制方程根本不需要涉及物理,“物理信息”只是一种命名法(而且这种技术无论如何都是物理学家最常用的)。如果你的系统是城市中的交通,并且你恰好有一个很好的数学模型,你希望神经网络的预测遵循该模型,那么物理信息神经网络非常适合你。
3、如何告知模型物理信息?
希望我已经说服了你,让模型了解控制我们系统的基础方程是值得的。但是,我们该怎么做呢?有几种方法可以做到这一点,但主要方法是调整损失函数,使其除了通常的数据相关部分之外,还有一个考虑控制方程的项。也就是说,损失函数 L 将由总和组成
![]()
这里,数据损失是通常的损失:均方差,或其他适合的损失函数形式;但方程部分是迷人的。想象一下你的系统由以下微分方程控制:
![]()
我们如何将其拟合到损失函数中?好吧,由于我们在训练神经网络时的任务是最小化损失函数,我们想要的是最小化以下表达式:
![]()
所以我们的方程相关损失函数结果是

也就是说,它是我们的 DE 的均方差。如果我们设法最小化这个值(即使这个项尽可能接近零),我们就会自动满足系统的控制方程。很聪明,对吧?
现在,需要解决损失函数中的额外项 L_IC:它考虑了系统的初始条件。如果没有提供系统的初始条件,则微分方程有无数个解。
例如,从地面扔出的球的轨迹由与从 10 楼扔出的球相同的微分方程控制;但是,我们确信这些球的路径不会相同。这里发生的变化是系统的初始条件。我们的模型如何知道我们正在讨论哪些初始条件?此时,我们自然会使用损失函数项来强制执行它!
对于我们的 DE,让我们规定当 t = 0 时,y = 1。因此,我们希望最小化初始条件损失函数,该函数的内容为:
![]()
如果我们最小化这个项,那么我们就会自动满足系统的初始条件。现在,剩下需要理解的是如何使用它来解决微分方程。
4、求解微分方程
如果神经网络既可以用损失函数的数据相关项进行训练(这通常是在经典架构中完成的),也可以用数据和方程相关项进行训练(这就是我刚才提到的物理信息神经网络),那么它一定可以训练为仅最小化方程相关项。这正是我们要做的!这里使用的唯一损失函数将是 L_equation。希望下面的图表能够说明我刚才所说的内容:今天我们的目标是右下角的模型类型,即我们的 DE 求解器 NN。
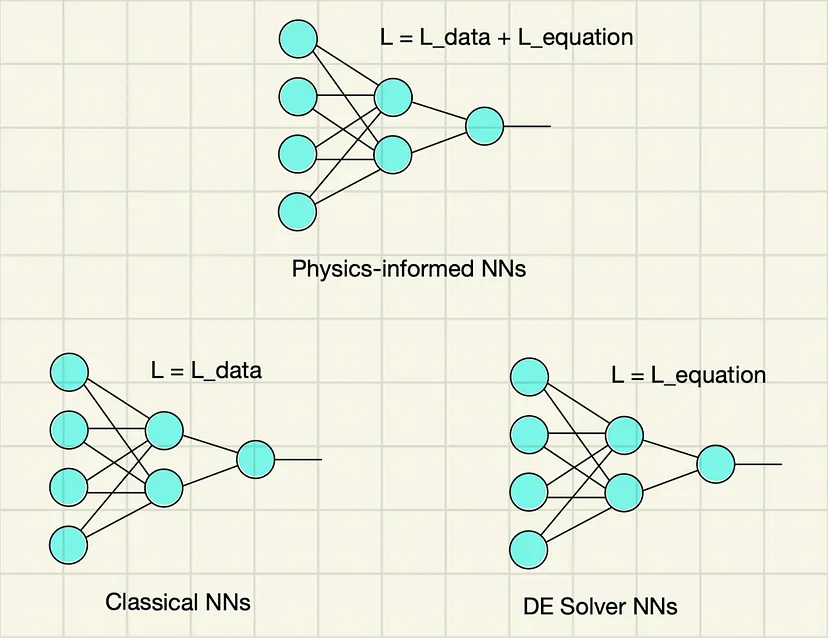
图 1:显示了各种神经网络及其损失函数的图表。在本文中,我们针对右下方的神经网络。
5、代码实现
为了展示我们刚刚学到的理论知识,我将使用机器学习的 PyTorch 库,在 Python 代码中实现所提出的解决方案。
首先要做的是创建一个神经网络架构:
import torch
import torch.nn as nn
class NeuralNet(nn.Module):
def __init__(self, hidden_size, output_size=1,input_size=1):
super(NeuralNet, self).__init__()
self.l1 = nn.Linear(input_size, hidden_size)
self.relu1 = nn.LeakyReLU()
self.l2 = nn.Linear(hidden_size, hidden_size)
self.relu2 = nn.LeakyReLU()
self.l3 = nn.Linear(hidden_size, hidden_size)
self.relu3 = nn.LeakyReLU()
self.l4 = nn.Linear(hidden_size, output_size)
def forward(self, x):
out = self.l1(x)
out = self.relu1(out)
out = self.l2(out)
out = self.relu2(out)
out = self.l3(out)
out = self.relu3(out)
out = self.l4(out)
return out这只是具有 LeakyReLU 激活函数的简单 MLP。然后,我将定义损失函数,以便在训练循环中稍后计算它们:
# Create the criterion that will be used for the DE part of the loss
criterion = nn.MSELoss()
# Define the loss function for the initial condition
def initial_condition_loss(y, target_value):
return nn.MSELoss()(y, target_value)现在,我们将创建一个用作训练数据的时间数组,并实例化模型,并选择一种优化算法:
# Time vector that will be used as input of our NN
t_numpy = np.arange(0, 5+0.01, 0.01, dtype=np.float32)
t = torch.from_numpy(t_numpy).reshape(len(t_numpy), 1)
t.requires_grad_(True)
# Constant for the model
k = 1
# Instantiate one model with 50 neurons on the hidden layers
model = NeuralNet(hidden_size=50)
# Loss and optimizer
learning_rate = 8e-3
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
# Number of epochs
num_epochs = int(1e4)最后,让我们开始训练循环:
for epoch in range(num_epochs):
# Randomly perturbing the training points to have a wider range of times
epsilon = torch.normal(0,0.1, size=(len(t),1)).float()
t_train = t + epsilon
# Forward pass
y_pred = model(t_train)
# Calculate the derivative of the forward pass w.r.t. the input (t)
dy_dt = torch.autograd.grad(y_pred,
t_train,
grad_outputs=torch.ones_like(y_pred),
create_graph=True)[0]
# Define the differential equation and calculate the loss
loss_DE = criterion(dy_dt + k*y_pred, torch.zeros_like(dy_dt))
# Define the initial condition loss
loss_IC = initial_condition_loss(model(torch.tensor([[0.0]])),
torch.tensor([[1.0]]))
loss = loss_DE + loss_IC
# Backward pass and weight update
optimizer.zero_grad()
loss.backward()
optimizer.step()请注意使用 torch.autograd.grad 函数自动对输出 y_pred 相对于输入 t 进行微分,以计算损失函数。
6、结果
经过训练,我们可以看到损失函数迅速收敛。图 2 显示了损失函数与 epoch 数的关系图,其中的插图显示了损失函数下降最快的区域。

图 2:按时期划分的损失函数。在插图中,我们可以看到收敛速度最快的区域。
你可能已经注意到,这个神经网络并不常见。它没有训练数据(我们的训练数据是手工制作的时间戳向量,这只是我们想要研究的时间域),因此它从系统获得的所有信息都以损失函数的形式出现。它的唯一目的是在它被设计用于解决的时间域内求解微分方程。因此,为了测试它,我们使用它训练的时间域是公平的。图 3 显示了 NN 预测与理论答案(即解析解)之间的比较。

图 3:所示神经网络预测和微分方程的解析解预测。
我们可以看到两者之间有相当好的一致性,这对神经网络来说非常好。
这种方法的一个缺点是它不能很好地概括未来的时间。图 4 显示了如果我们将时间数据点向前移动五步会发生什么,结果简直是一片混乱。
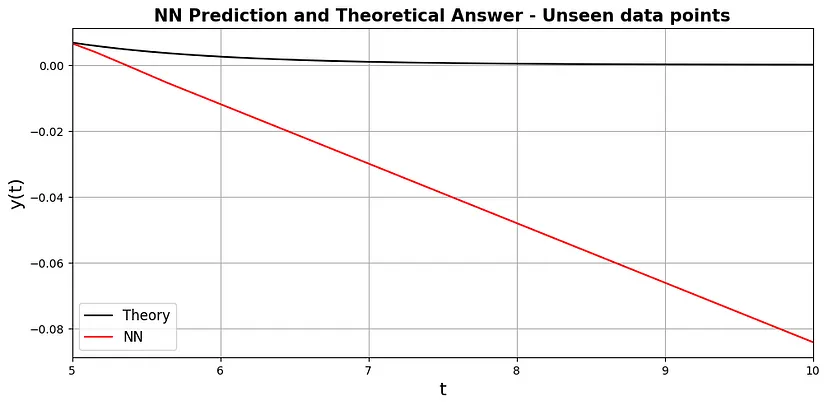
图 4:神经网络和未见数据点的解析解。
因此,这里的教训是,这种方法是作为时间域内微分方程的数值求解器,不应将其用作常规神经网络,使用未见的训练域外数据进行预测并期望它能很好地推广。
7、结束语
毕竟,还有一个问题是:
为什么要费心训练一个不能很好地推广到未见数据的神经网络,而且它显然比解析解更差,因为它有内在的统计误差?
首先,这里提供的示例是一个微分方程的示例,其解析解是已知的。对于未知的解,仍然必须使用数值方法。话虽如此,用于微分方程求解的数值方法通常会累积误差。这意味着如果你试图在许多时间步骤中求解方程,解将在此过程中失去其准确性。另一方面,神经网络求解器学习如何在其每个训练时期为所有数据点求解 DE。
另一个原因是神经网络是良好的插值器,因此如果你想知道看不见的数据中的函数值(但这种“看不见的数据”必须位于你训练的时间间隔内),神经网络将迅速为你提供经典数值方法无法迅速给出的值。
原文链接:用神经网络求解微分方程 - BimAnt