浮点数运算

引言

浮点数在计算机中难以进行精确表示，例如：0.1 换算成二进制是一个无限循环的小数，无论是double 还是float，都只能存储一个近似的值。但是0.5却可以进行精确的表示。

误差

浮点数的运算时常伴有误差：

public class Hello {
	public static void main(String[] args) {
		double x = 1.0 / 10;
		double y = 1 - 9.0 / 10;
		System.out.println(x);
		System.out.println(y);		
	}
}

结果如下：

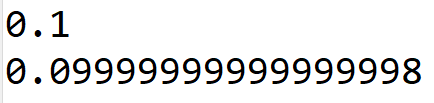
同样的，比较两个浮点数，也会发生误差：

public class Hello {
	public static void main(String[] args) {
		double x = 1.0 / 10;
		double y = 1 - 9.0 / 10;
		System.out.println(x == y);
	}
}

输出：false

正确的判断两个浮点数是否相等的方法是判断两个浮点数的差是否小于一个很小的数。

public class Hello {
	public static void main(String[] args) {
		double x = 1.0 / 10;
		double y = 1 - 9.0 / 10;
		double sub = Math.abs(x - y);
		if (sub < 1e-5) {
			System.out.println("相等！");
		} else {
			System.out.println("不相等！");
		}
	}
}

输出：相等

浮点数在计算机内存中的表示方法比整数要复杂，且完全遵循IEEE-754标准。

类型提升

需要注意的是，整数和浮点数进行运算也会自动类型提升，变成一个浮点数。

public class Hello {
	public static void main(String[] args) {
		int x = 10;
		float y = 1f;
		System.out.println(x + y);	// 输出 11.0
	}
}

但是，整数之间的运算是不会自动提升类型的，在复杂的四则运算中也是如此。

// 计算1 + .. + 100
public class Hello {
	public static void main(String[] args) {
		System.out.println(1f + 24 / 5);	// 输出 5.0
	}
}

可见，式子中的 24 / 5 = 4，4 + 1f = 5f，最后输出了 5.0

溢出

如果你用浮点数除以 0，不会得到报错，而是会得到几个奇怪的值。

public class Hello {
	public static void main(String[] args) {
		System.out.println(1f / 0);	 // Infinity
		System.out.println(0.0 / 0); // NaN
		System.out.println(-1f / 0); //	-Infinity
	}
}

• NaN表示 Not a Number
• Infinity 表示无限
• -Infinity表示负无限

强制转型

将浮点型强制转成整型会抹去小数点后面的数，如果超过整型能表示的最大范围，只会返回整型的最大值。

public class Hello {
	public static void main(String[] args) {
		int x = (int) 12.7;
		System.out.println(x);
		
		int y = (int) -12.7;
		System.out.println(y);	// 转型后抹去小数部分
		
		int z = (int) 1.2e20;
		System.out.println(z);	// 溢出会返回整型的最大值
	}
}

如果需要进行四舍五入，可以对浮点数加上 0.5 后进行转型。

public class Hello {
	public static void main(String[] args) {
		int x = (int) (1.2f + 0.5);	// 得到 1
		System.out.println(x);
		
		int y = (int) (1.6f + 0.5);	// 得到 2
		System.out.println(y);
	}
}

练习

根据一元二次方程的求根公式，计算出方程的两个解。

答案

public class Hello {
	public static void main(String[] args) {
		double a = 1.0;
		double b = 3.0;
		double c = -4.0;
		double ans1 = (-b + Math.sqrt(b * b - 4 * a * c))/(2*a);
		double ans2 = (-b - Math.sqrt(b * b - 4 * a * c))/(2*a);
		
		System.out.println(ans1);	// 1.0
		System.out.println(ans2);	// -4.0
	}
}